5.2.2: Conversiones de Rectangular a Polar

Última actualización
Guardar como PDF

Page ID: 107744

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Convertir de coordenadas cartesianas a polares

Trig Riddle: Yo soy el punto\((1,−3)\). ¿Cuáles son mis coordenadas polares?

Relaciones trigonométricas de puntos

Cualquier punto en el plano de coordenadas se puede representar por su ángulo de rotación y radio, o distancia desde el origen. Se dice que el punto se encuentra en el lado terminal del ángulo. Podemos encontrar la medida del ángulo de referencia usando trigonometría de triángulo rectángulo. Cuando se identifica el punto de esta manera llamamos coordenadas polares a las coordenadas. Se escriben como\((r,\theta )\), donde\(r\) está el radio y\(\theta \) es el ángulo de rotación. El ángulo de rotación se puede dar en grados o radianes.

Busquemos el ángulo de rotación (en grados) y el radio (distancia desde el origen) del punto\((−3,6)\).

Primero, haz un boceto, traza el punto y suelta una perpendicular al eje x para hacer un triángulo rectángulo.

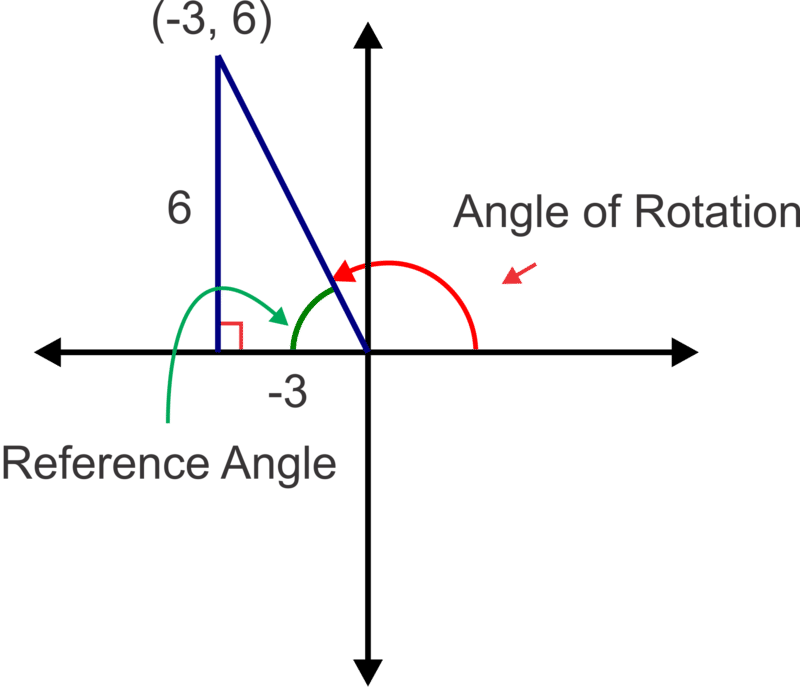
f-d_a3e37b4d8061317b75544bca369aee46808633312c10174c1e08fba2+image_tiny+imagen_tiny.png — Figura\(\PageIndex{1}\)

Del boceto, podemos ver que\(\tan^{-1}(−63)=63.4^{\circ}\) es el ángulo de referencia por lo que es el ángulo de rotación\(180^{\circ}−63.4^{\circ}=116.6^{\circ}\).

El radio o distancia desde el origen es la hipotenusa del triángulo rectángulo.

\(\begin{aligned} r^2 &=(−3)2+(6)2\\ r^2 &=45\\ r&=\sqrt{45}=3 \sqrt{5}\end{aligned}\)

Usando esta información, podemos escribir el punto\((−3,6)\) en forma de coordenadas polares como\((3\sqrt{5}, 116.6^{\circ})\)

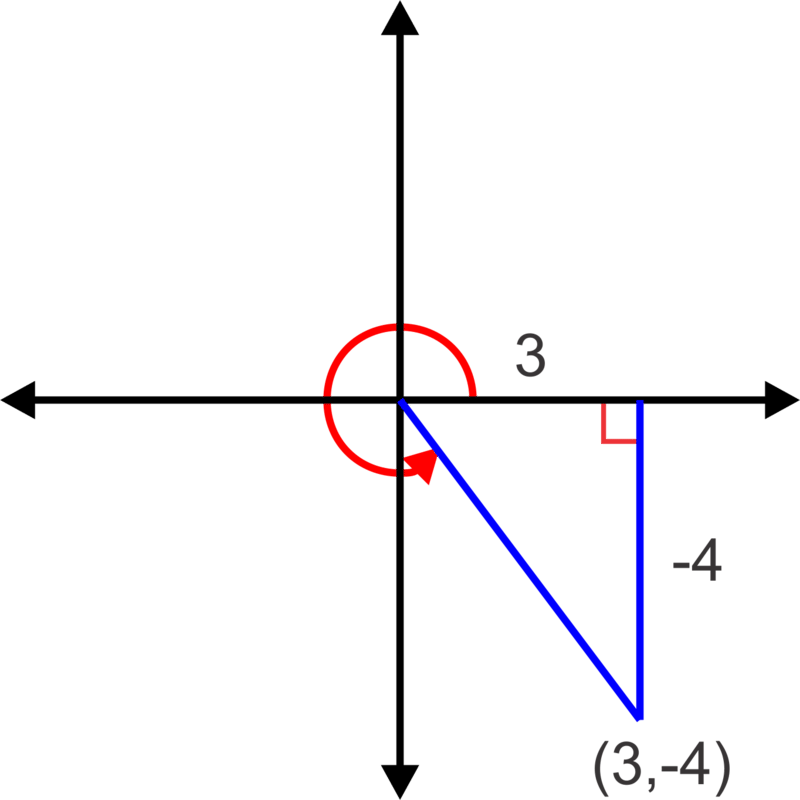
Ahora, escribamos las coordenadas cartesianas,\((3,−4)\), en forma Polar y demos el ángulo en grados.

Nuevamente, comience con un boceto.

Podemos encontrar el ángulo de referencia nuevamente usando tangente:\(\tan^{-1}\left(\dfrac{−4}{3}\right)=−53.1^{\circ}\). Entonces el ángulo de rotación es\(360^{\circ}−53.1^{\circ}=306.9^{\circ}\)

Ahora encuentra el radio:

\(\begin{aligned} r^2 &=3^2+(−4)^2\\ r^2 &=25 \\ r&=\sqrt{25}=5 \end{aligned}\)

Las coordenadas polares son así\((5, 306.9^{\circ})\)

f-d_cc7272cbe2d522cf016ca26e9826ea7f41da801d5bfd024e24073787+image_tiny+image_tiny+image_tiny.png — Figura\(\PageIndex{2}\)

Nota: Es posible que hayas notado que hay un patrón que nos da un atajo para encontrar las coordenadas polares para cualquier coordenadas cartesianas,\((x,y)\):

El ángulo de referencia se puede encontrar usando,\(\theta =\tan^{-1}\left(\dfrac{y}{x}\right)\) y luego el ángulo de rotación se puede encontrar colocando el ángulo de referencia en el cuadrante apropiado y dando un ángulo de rotación positivo desde el eje x — positivo (\(0^{\circ}\leq \theta <360^{\circ}\)o\(0\leq \theta <2\pi\)). El radio es siempre\(r=\sqrt{x^2+y^2}\) y debe darse en forma radical reducida.

Finalmente, dado el punto (−9, −5) en el lado terminal de un ángulo, vamos a encontrar las coordenadas polares (en radianes) del punto y las seis relaciones trigonométricas para el ángulo.

Asegúrate de que tu calculadora esté en modo radianes. Usando el atajo, podemos encontrar las coordenadas Polar:

\(\tan^{-1}\left(\dfrac{5}{9}\right)=0.51\). Dado que x e y son ambos negativos, el punto se encuentra en el tercer cuadrante que hace el ángulo de rotación\(\pi +0.51=3.65\). El radio será\(r=\sqrt{9^2+5^2}=\sqrt{106}\). Las coordenadas polares son\((\sqrt{106}, 3.65)\). En cuanto a las seis relaciones trigonométricas, un diagrama nos ayudará a:

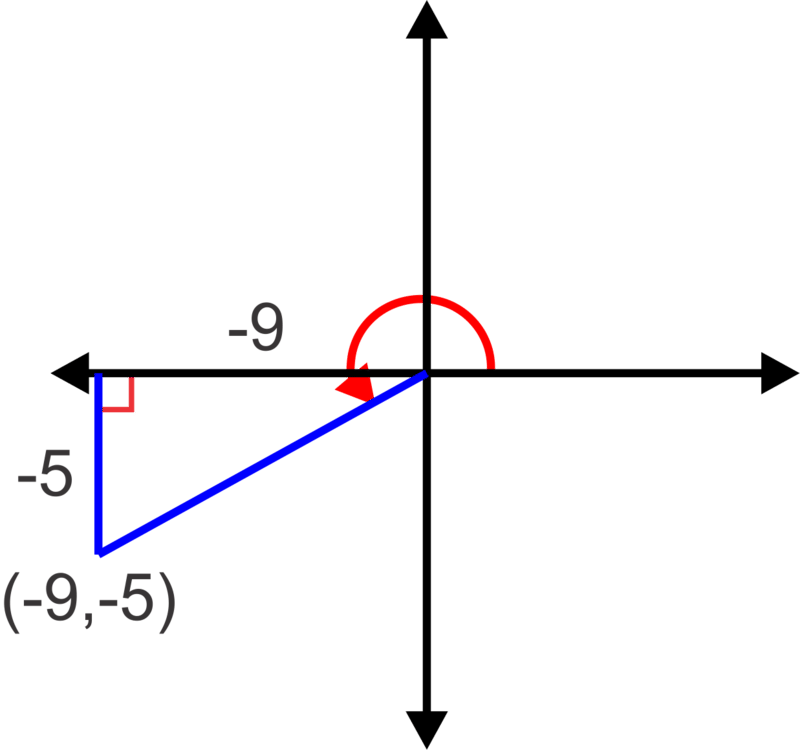
f-d_d8c3e19522e8c0b61f03c091797d20dd42cbff1b6ca032a9f59a8346+image_tiny+image_tiny.png — Figura\(\PageIndex{3}\)

Eso ya lo sabemos\(\tan 3.65=\dfrac{5}{9}\), entonces\(\cot 3.65=\dfrac{9}{5}\).

Ahora podemos usar la hipotenusa,\(\sqrt{106}\) para encontrar las otras proporciones:

\(\sin 3.65=\dfrac{−5}{\sqrt{106}}=−\dfrac{5 \sqrt{106}}{106}\)y\(\csc 3.65=\dfrac{\sqrt{−106}}{5}\).

\(\cos 3.65=\dfrac{−9}{\sqrt{106}}=−\dfrac{9\sqrt{106}}{106}\)y\(\sec 3.65=−\dfrac{\sqrt{106}}{9}\)

Ejemplo\(\PageIndex{1}\)

Antes, se le pidió que encontrara las coordenadas polares del punto\((1,−3)\).

Solución

Primero, haz un boceto, traza el punto y suelta una perpendicular al eje x para hacer un triángulo rectángulo.

Del boceto, podemos ver que\(\tan^{-1}(−31)=71.6^{\circ}\) es el ángulo de referencia. El punto\((1,−3)\) está en el segundo cuadrante, por lo que el ángulo de rotación está\(180^{\circ}−71.6^{\circ}=108.4^{\circ}\).

El radio o distancia desde el origen es la hipotenusa del triángulo rectángulo.

\ (\ begin {alineado}
r^ {2} & =( 1) ^ {2} + (-3) ^ {2}\\
r^ {2} &=10\\
r &=\ sqrt {10}
\ end {alineado}\)

Por lo tanto, mis coordenadas polares son\((\sqrt{10},108.4^{\circ})\).

Ejemplo\(\PageIndex{2}\)

Encuentra el ángulo de rotación (en grados) y el radio (distancia desde el origen) del punto\((7,24)\).

Solución

\(r=\sqrt{7^2+24^2}=25\),\(\theta =\tan^{-1}\left(\dfrac{24}{7}\right) \approx 73.7^{\circ}\)

Ejemplo\(\PageIndex{3}\)

Escribe las coordenadas cartesianas, (−8, −15), en forma Polar (en radianes) y encuentra las seis relaciones trigonométricas para el ángulo.

Solución

\(r=\sqrt{(−8)^2+(−15)^2}=17\)y\(\theta =\tan^{−1}\left(\dfrac{−15}{−8}\right)\approx 1.08\) así lo son las coordenadas polares\((17,1.08)\).

Las seis relaciones trigonométricas son:

\ (\ begin {array} {ll}
\ sin 1.08=-\ dfrac {15} {17} &\ csc 1.08=-\ dfrac {17} {15}\
\ cos 1.08=-\ dfrac {8} {17} &\ seg 1.08=-\ dfrac {8} {15} {15}
\\ tan 1.08=\ dfrac {15} 8} &\ cot 1.08=-\ dfrac {8} {15}
\ end {array}\)

Ejemplo\(\PageIndex{4}\)

Dado el punto\((12,−4)\) en el lado terminal de un ángulo, encuentra las coordenadas polares (en grados) del punto y las seis relaciones trigonométricas para el ángulo.

Solución

\(r=\sqrt{12^2+(−4)^2} =4\sqrt{10}\)y\(\theta =\tan^{−1}\left(\dfrac{−4}{12}\right)\approx 341.6^{\circ}\) así lo son las coordenadas polares\((4\sqrt{10}, 341.6^{\circ})\).

Las seis relaciones trigonométricas son:

\ (\ begin {alineado}
\ sin 341.6^ {\ circ} &=-\ dfrac {\ sqrt {10}} {10} &\ csc 341.6^ {\ circ} &=-\ sqrt {10}\
\ cos 341.6^ {\ circ} &=\ dfrac {3\ sqrt {10}} {10} &\ csc 341.6^ {\ circ} &=\ dfrac {\ sqrt {10}} {3}\\
\ tan 341.6^ {\ circ} &=-\ dfrac {1} {3} &\ tan 341. 6^ {\ circ} &=-3
\ end {alineado}\)

Revisar

Las medidas de ángulo deben redondearse al grado más querido o centésima parte de un radián o darse exactamente si es posible. Todos los valores de r deben darse en forma de radicales reducidos.

Escribe los siguientes pares de coordenadas cartesianas en forma Polar. Utilizar grados para problemas 1 y 2 y radianes para problemas 3-5.

\((16,−30)\)
\((5,5)\)
\((−5,−12)\)
\((−9,40)\)
\((−4,8)\)

Dados los puntos en el lado terminal de un ángulo, encontrar las coordenadas polares (en grados) del punto y las seis relaciones trigonométricas para los ángulos.

\((−6,8)\)
\((0,−15)\)
\((10,−8)\)
\((4\sqrt{3},4)\)
\((−6,6)\)

Dados los puntos en el lado terminal de un ángulo, encontrar las coordenadas polares (en radianes) del punto y las seis relaciones trigonométricas para los ángulos.