5.2.6: Sistemas de Ecuaciones Polares
- Page ID
- 107749
Puntos de intersección o ubicaciones donde dos ecuaciones polares tienen la misma solución.
Probablemente recuerde que cuando grafica múltiples ecuaciones en la misma línea, generalmente termina con ubicaciones en la gráfica donde se cruzan (¡a menos que esté graficando líneas paralelas!).
Lo mismo ocurre cuando se grafican ecuaciones en forma polar, y/o en una gráfica polar. Cuando graficas la intersección de múltiples ecuaciones polares, las tratas tal como lo harías con ecuaciones rectangulares, graficas ambas y encuentras las áreas que son verdaderas para ambas ecuaciones.
Sistemas de Ecuaciones Polares
Las ecuaciones polares se pueden graficar usando coordenadas polares. Graficar dos ecuaciones polares en el mismo conjunto de ejes puede resultar en tener punto (s) de intersección.
Todos los puntos de una gráfica polar son coordenadas que hacen válida la ecuación. Las coordenadas del punto (s) de intersección cuando se sustituyan en cada ecuación harán que ambas ecuaciones sean válidas.
Un método para encontrar punto (s) de intersección para dos gráficas polares es establecer las ecuaciones iguales entre sí.
Llama a la primera ecuación\(r_1 \) y a la segunda ecuación\(r_2 \).
Los puntos de intersección son cuándo\(r_1 = r_2 \), así que establece las ecuaciones iguales y luego resuelve la ecuación trigonométrica resultante.
Encuentra la intersección de\(r_1 =3 \sin \theta \) y\(r_2 =\sqrt{3} \cos \theta \).
Solución
Establezca las ecuaciones iguales entre sí:\(3 \sin \theta =\sqrt{3} \cos \theta\)
dividir ambos lados de la ecuación por cos\(\theta \) y 3:\(\dfrac{3 \sin \theta }{3\cos \theta }=\dfrac{\sqrt{3} \cos \theta }{3 \cos \theta}\)
Simplificar:\(\dfrac{\sin \theta }{\cos \theta }=\dfrac{\sqrt{3} }{3}\)
Usa la identidad:\(\dfrac{\sin \theta }{\cos \theta }=\tan \theta\)
\(\tan \theta =\dfrac{\sqrt{3}}{ 3}\)
\(\theta =\dfrac{\pi }{6}\)o\(\dfrac{7\pi }{6}\)
sustituir\(\dfrac{\pi }{6}\) en cualquiera de las ecuaciones para obtener\(r = 1.5\)
sustituir\(\dfrac{7\pi }{6}\) en cualquiera de las ecuaciones para obtener\(-1.5\)
NOTA: las coordenadas\(\left(1.5, \dfrac{\pi }{6}\right)\) y\(\left(−1.5, \dfrac{7\pi }{6}\right)\) representan el MISMO punto polar por lo que solo hay una solución a esta ecuación.
¿Ya terminamos? Si miramos las gráficas de\(r_1 \) y\(r_2 \), podemos ver que hay otro punto de intersección:
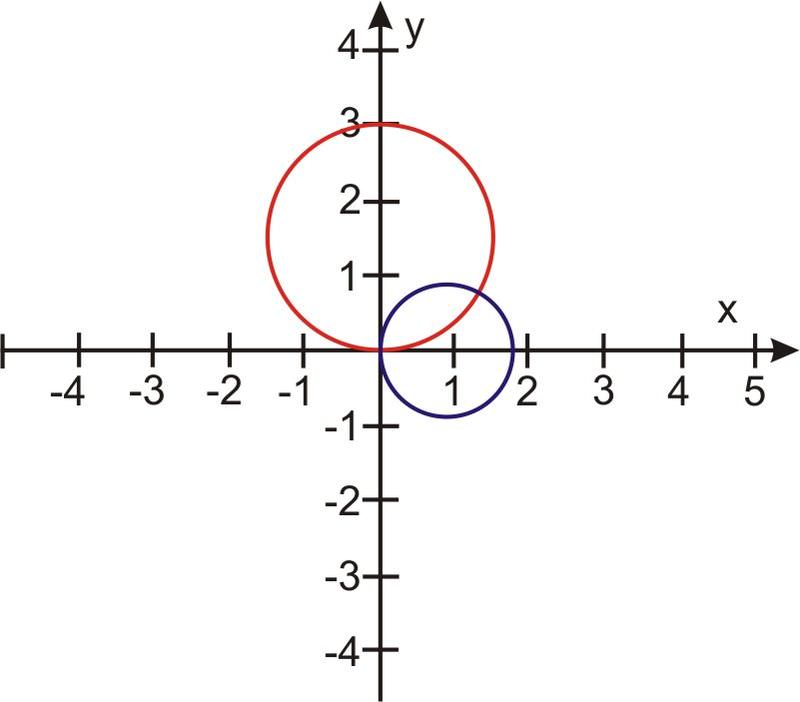
cuando\(\theta = 0\),\(r_1 = 3 \) pecado\(\theta = 3 \) pecado\((0) = 0\)
Eso significa que el\(r_1 = 3 \) pecado\(\theta\) pasa por el poste\((0, 0)\).
Para r_2: cuando\(\theta =\dfrac{\pi }{2}\), es\(r_2 = 0\) decir\(r_2 =\sqrt{3} \cos \theta \) pasa por el punto\(\left(0,\dfrac{\pi }{2}\right)\).
Por lo tanto, ambas gráficas pasan por el polo y el polo es un punto de intersección.
¡El poste NO fue revelado como un punto de intersección usando el primer paso! (¿Por qué? Pista: ¿Cuántas formas hay de representar el polo en coordenadas polares?) Esto nos muestra que después de usar métodos algebraicos para encontrar intersecciones en puntos distintos al polo, también se debe verificar si hay intersecciones en el polo.
Encuentra el punto (s) de intersección para las dos gráficas:\(r_1 = 1\) y\(r_2 = 2 \sin 2\theta \).
Solución
Establecer\(r_1 = r_2\) y resolver:
\(\begin{aligned} 1&=2 \sin 2\theta \\ \dfrac{1}{2}&=\sin 2\theta\end{aligned} \)
Usa una sustitución\(\alpha = 2\theta \) para resolver
\(\begin{aligned} \dfrac{1}{2}&=\sin \alpha \\ \alpha &=\dfrac{\pi }{6}, \dfrac{5\pi }{6} \end{aligned}\)
Ya que\(\alpha = 2\theta \), resolver para nos\(\theta \) da
\(\theta =\dfrac{\pi }{12}, \dfrac{5\pi }{12}\)
Pero, recordemos que\(\theta \) tiene el rango\(0 \leq \theta \leq 2\pi \). Ya que\(0 \leq \alpha \leq 2\pi\) resolvimos con realmente necesitamos considerar valores de\(\theta \) con\(0 \leq \theta \leq 4\pi \). ¿Por qué? Recordemos que\(\sin (2\theta )\) tiene dos ciclos entre\(0\) y\(2\pi \), y así sumamos dos soluciones más,
\(\alpha =\dfrac{13\pi }{6}, \dfrac{17\pi }{6}\)
y desde entonces\(\alpha = 2\theta \),
\(\theta =\dfrac{13\pi }{12}, \dfrac{17\pi }{12}\)
Por último, debemos considerar soluciones cuando\(r = -1\) porque\(r = 1\) y\(r = -1\) son la misma ecuación polar. Entonces, resolviendo
\(\begin{aligned} −\dfrac{1}{2}&=\sin \alpha \\ \alpha &=\dfrac{7\pi }{6}, \dfrac{11\pi }{6}\end{aligned}\)
Nuevamente, usar\(\alpha = 2\theta \) y agregar soluciones para la repetición nos da cuatro soluciones más,
\(\theta =\dfrac{7\pi }{12}, \dfrac{11\pi }{12}, \dfrac{19\pi }{12}, \dfrac{21\pi}{12}\)
Entonces, en total, hay ocho soluciones a este conjunto de ecuaciones.
NOTA: Recordemos que resolver ecuaciones trigonométricas donde el ángulo es\ theta requiere mirar todos los valores potenciales entre 0 y\(2\pi \). Cuando el ángulo es\(2\theta\) como es en este caso, asegúrese de buscar todos los valores potenciales entre 0 y\(4\pi \). Cuando el ángulo es\(3\theta\) como es en este caso, asegúrese de buscar todos los valores potenciales entre 0 y\(6\pi \)., y así sucesivamente.
Dado que\(r_1 \) no puede ser igual a 0, el polo no está en su gráfica y no es un punto de intersección.
La gráfica revela ocho puntos de intersección que se encontraron anteriormente.
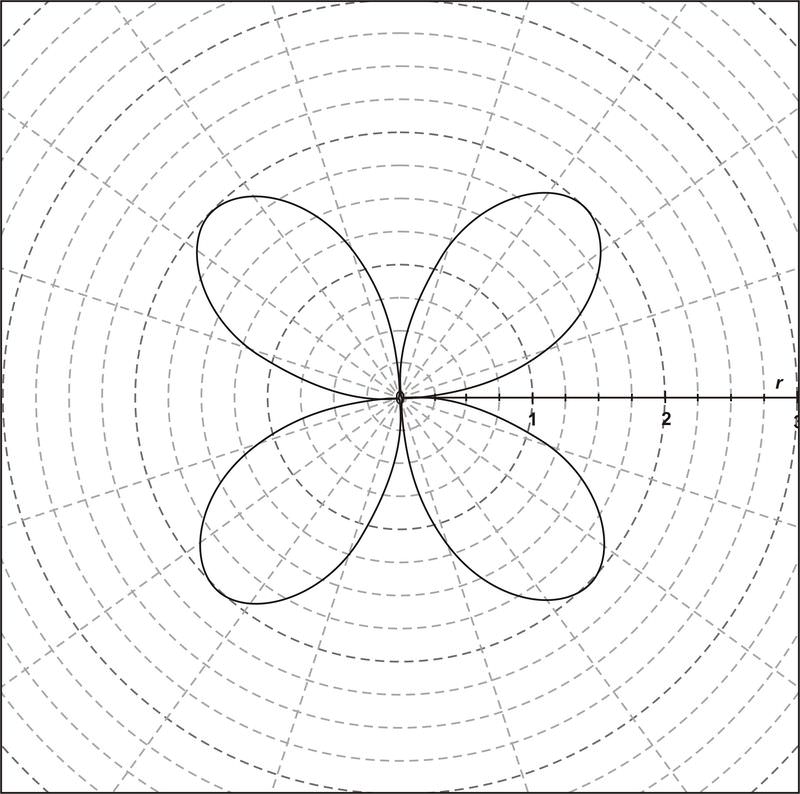
Encontrar punto (s) de intersección, si existe alguno, para el siguiente par de ecuaciones:\(r_1 = 2\) y\(r_2 = \sec \theta \).
Aquí utilizaremos una tabla de valores para cada función, resolviendo por cuadrante. Recordemos que el periodo de\(\sec \theta\) es\(2\pi \).
Solución
Para el primer cuadrante:
| \(\theta\)(ángulo) | 0 | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) |
|---|---|---|---|---|---|
| \ (\ theta\) (ángulo)” class="lt-k12-4182">\(r_1\) (distancia) | 2 | \ (\ dfrac {\ pi} {6}\)” class="lt-k12-4182">2 | \ (\ dfrac {\ pi} {4}\)” class="lt-k12-4182">2 | \ (\ dfrac {\ pi} {3}\)” class="lt-k12-4182">2 | \ (\ dfrac {\ pi} {2}\)” class="lt-k12-4182">2 |
| \ (\ theta\) (ángulo)” class="lt-k12-4182">\(r_2\) | 1 | \ (\ dfrac {\ pi} {6}\)” class="lt-k12-4182">1.15 | \ (\ dfrac {\ pi} {4}\)” class="lt-k12-4182">1.4 | \ (\ dfrac {\ pi} {3}\)” class="lt-k12-4182">2 | \ (\ dfrac {\ pi} {2}\)” class="lt-k12-4182">und |
Para el segundo cuadrante:
| \(\theta\)(ángulo) | \(\dfrac{2 \pi}{3}\) | \(\dfrac{3 \pi}{4}\) | \(\dfrac{5 \pi}{6}\) | \(\pi\) |
|---|---|---|---|---|
| \ (\ theta\) (ángulo)” class="lt-k12-4182">\(r_1\) (distancia) | \ (\ dfrac {2\ pi} {3}\)” class="lt-k12-4182">2 | \ (\ dfrac {3\ pi} {4}\)” class="lt-k12-4182">2 | \ (\ dfrac {5\ pi} {6}\)” class="lt-k12-4182">2 | \ (\ pi\)” class="lt-k12-4182">2 |
| \ (\ theta\) (ángulo)” class="lt-k12-4182">\(r_2\) | \ (\ dfrac {2\ pi} {3}\)” class="lt-k12-4182">-2 | \ (\ dfrac {3\ pi} {4}\)” class="lt-k12-4182">-1.4 | \ (\ dfrac {5\ pi} {6}\)” class="lt-k12-4182">-1.15 | \ (\ pi\)” class="lt-k12-4182">-1 |
Para el tercer cuadrante:
| \(\theta\)(ángulo) | \(\dfrac{7 \pi}{6}\) | \(\dfrac{5 \pi}{4}\) | \(\dfrac{4 \pi}{3}\) | \(\dfrac{3 \pi}{2}\) |
|---|---|---|---|---|
| \ (\ theta\) (ángulo)” class="lt-k12-4182">\(r_1\) (distancia) | \ (\ dfrac {7\ pi} {6}\)” class="lt-k12-4182">2 | \ (\ dfrac {5\ pi} {4}\)” class="lt-k12-4182">2 | \ (\ dfrac {4\ pi} {3}\)” class="lt-k12-4182">2 | \ (\ dfrac {3\ pi} {2}\)” class="lt-k12-4182">2 |
| \ (\ theta\) (ángulo)” class="lt-k12-4182">\(r_2\) | \ (\ dfrac {7\ pi} {6}\)” class="lt-k12-4182">-1.15 | \ (\ dfrac {5\ pi} {4}\)” class="lt-k12-4182">-1.4 | \ (\ dfrac {4\ pi} {3}\)” class="lt-k12-4182">-2 | \ (\ dfrac {3\ pi} {2}\)” class="lt-k12-4182">und |
Para el cuarto cuadrante:
| \(\theta\)(ángulo) | \(\dfrac{5 \pi}{3}\) | \(\dfrac{7 \pi}{4}\) | \(\dfrac{11 \pi}{6}\) | \(2\pi\) |
|---|---|---|---|---|
| \ (\ theta\) (ángulo)” class="lt-k12-4182">\(r_1\) (distancia) | \ (\ dfrac {5\ pi} {3}\)” class="lt-k12-4182">2 | \ (\ dfrac {7\ pi} {4}\)” class="lt-k12-4182">2 | \ (\ dfrac {11\ pi} {6}\)” class="lt-k12-4182">2 | \ (2\ pi\)” class="lt-k12-4182">2 |
| \ (\ theta\) (ángulo)” class="lt-k12-4182">\(r_2\) | \ (\ dfrac {5\ pi} {3}\)” class="lt-k12-4182">2 | \ (\ dfrac {7\ pi} {4}\)” class="lt-k12-4182">1.4 | \ (\ dfrac {11\ pi} {6}\)” class="lt-k12-4182">1.15 | \ (2\ pi\)” class="lt-k12-4182">1 |
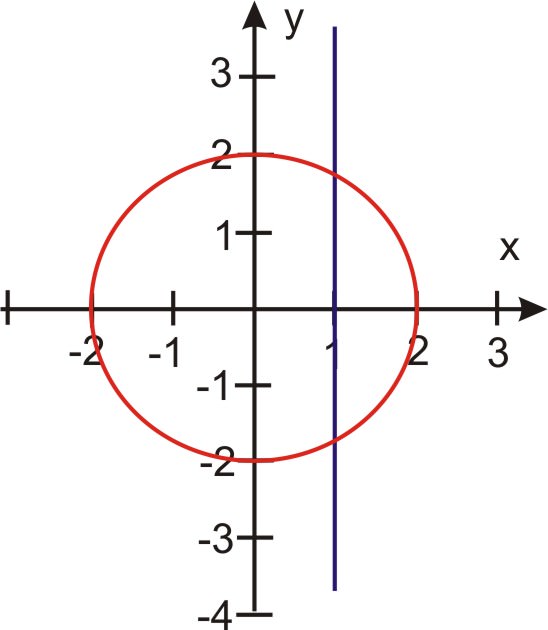
Obsérvese que los cuadrantes 3º y 4º repiten los valores del cuadrante 1º y 2º.
Observe en la tabla de valores que\(\left(2, \dfrac{\pi}{3}\right)\) y\(\left(2, \dfrac{5 \pi}{3}\right)\) son los puntos de intersección. Mira las curvas- la primera ecuación produce un círculo mientras que la segunda produce una línea. El número máximo de puntos de intersección para una línea y un círculo es 2. Se han encontrado los dos puntos.
Encuentra el (los) punto (s) de intersección para este par de ecuaciones polares:\(r = 2 + 4 \sin \theta\) y\(\theta = 60^{\circ}\).
Solución
La ecuación\(\theta = 60^{\circ}\) es una línea que forma un\(60^{\circ}\) ángulo con el eje r.
Hacer una tabla de valores para\(r = 2 + 4 \sin \theta\)
Para el primer cuadrante:
| \(\theta\)(ángulo) | 0 | 30 | 45 | 60 | 90 |
|---|---|---|---|---|---|
| \ (\ theta\) (ángulo)” class="LT-K12-4182">R (distancia) | 2 | 4 | 4.83 | 5.46 | 6 |
Para el segundo cuadrante:
| \(\theta\)(ángulo) | 120 | 135 | 150 | 180 |
|---|---|---|---|---|
| \ (\ theta\) (ángulo)” class="LT-K12-4182">R (distancia) | 5.46 | 4.83 | 4 | 2 |
Para el tercer cuadrante:
| \(\theta\)(ángulo) | 210 | 225 | 240 | 270 |
|---|---|---|---|---|
| \ (\ theta\) (ángulo)” class="LT-K12-4182">R (distancia) | 0 | -.83 | -1.46 | -2 |
Para el cuarto cuadrante:
| \(\theta\)(ángulo) | 300 | 315 | 330 | 360 |
|---|---|---|---|---|
| \ (\ theta\) (ángulo)” class="LT-K12-4182">R (distancia) | -1.46 | -.83 | 0 | 2 |
Observe que hay dos soluciones en la tabla.,\((60, 5.46)\) y\((240, -1.46) = (60, 1.46)\). Recordemos que cuando\(r < 0\), trazar un punto\((r, \theta )\), girando\(180^{\circ}\) (o\(\pi\)).
Por último, tenemos que revisar el poste:\(r = 2 + 4 \sin \theta \) pasa a través del poste para\(\theta = 330^{\circ}\), y\(\theta = 60^{\circ}\) también pasa por el poste. Así, el tercer punto de intersección es\((0, 0)\).
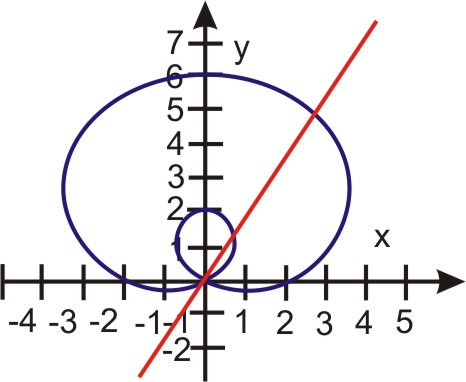
Encuentra el (los) punto (s) de intersección para este par de ecuaciones polares:\(r_1 = 2 \cos \theta\) y\(r_2 = 1\).
Solución
Hacer una mesa:
Para el primer cuadrante:
| \(\theta\)(ángulo) | 0 | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) |
|---|---|---|---|---|---|
| \ (\ theta\) (ángulo)” class="lt-k12-4182">\(r_1\) (distancia) | 2 | \ (\ dfrac {\ pi} {6}\)” class="lt-k12-4182">\(\sqrt{3}\) | \ (\ dfrac {\ pi} {4}\)” class="lt-k12-4182">\(\sqrt{2}\) | \ (\ dfrac {\ pi} {3}\)” class="lt-k12-4182">1 | \ (\ dfrac {\ pi} {2}\)” class="lt-k12-4182">0 |
| \ (\ theta\) (ángulo)” class="lt-k12-4182">\(r_2\) | 1 | \ (\ dfrac {\ pi} {6}\)” class="lt-k12-4182">1 | \ (\ dfrac {\ pi} {4}\)” class="lt-k12-4182">1 | \ (\ dfrac {\ pi} {3}\)” class="lt-k12-4182">1 | \ (\ dfrac {\ pi} {2}\)” class="lt-k12-4182">1 |
Para el segundo cuadrante:
| \(\theta\)(ángulo) | \(\dfrac{2 \pi}{3}\) | \(\dfrac{3 \pi}{4}\) | \(\dfrac{5 \pi}{6}\) | \(\pi\) |
|---|---|---|---|---|
| \ (\ theta\) (ángulo)” class="lt-k12-4182">\(r_1\) (distancia) | \ (\ dfrac {2\ pi} {3}\)” class="lt-k12-4182">-1 | \ (\ dfrac {3\ pi} {4}\)” class="lt-k12-4182">\(−\sqrt{2}\) | \ (\ dfrac {5\ pi} {6}\)” class="lt-k12-4182">\(−\sqrt{3}\) | \ (\ pi\)” class="lt-k12-4182">-2 |
| \ (\ theta\) (ángulo)” class="lt-k12-4182">\(r_2\) | \ (\ dfrac {2\ pi} {3}\)” class="lt-k12-4182">1 | \ (\ dfrac {3\ pi} {4}\)” class="lt-k12-4182">1 | \ (\ dfrac {5\ pi} {6}\)” class="lt-k12-4182">1 | \ (\ pi\)” class="lt-k12-4182">1 |
Para el tercer cuadrante:
| \(\theta\)(ángulo) | \(\dfrac{7 \pi}{6}\) | \(\dfrac{5 \pi}{4}\) | \(\dfrac{4 \pi}{3}\) | \(\dfrac{3 \pi}{2}\) |
|---|---|---|---|---|
| \ (\ theta\) (ángulo)” class="lt-k12-4182">\(r_1\) (distancia) | \ (\ dfrac {7\ pi} {6}\)” class="lt-k12-4182">\(−\sqrt{3}\) | \ (\ dfrac {5\ pi} {4}\)” class="lt-k12-4182">\(−\sqrt{2}\) | \ (\ dfrac {4\ pi} {3}\)” class="lt-k12-4182">-1 | \ (\ dfrac {3\ pi} {2}\)” class="lt-k12-4182">0 |
| \ (\ theta\) (ángulo)” class="lt-k12-4182">\(r_2\) | \ (\ dfrac {7\ pi} {6}\)” class="lt-k12-4182">1 | \ (\ dfrac {5\ pi} {4}\)” class="lt-k12-4182">1 | \ (\ dfrac {4\ pi} {3}\)” class="lt-k12-4182">1 | \ (\ dfrac {3\ pi} {2}\)” class="lt-k12-4182">1 |
Para el cuarto cuadrante:
| \(\theta\)(ángulo) | \(\dfrac{5 \pi}{3}\) | \(\dfrac{7 \pi}{4}\) | \(\dfrac{11 \pi}{6}\) | \(2\pi\) |
|---|---|---|---|---|
| \ (\ theta\) (ángulo) ">\(r_1\) (distancia) | \ (\ dfrac {5\ pi} {3}\) ">1 | \ (\ dfrac {7\ pi} {4}\) ">\(\sqrt{2}\) | \ (\ dfrac {11\ pi} {6}\) ">\(\sqrt{3}\) | \ (2\ pi\) ">2 |
| \ (\ theta\) (ángulo) ">\(r_2\) | \ (\ dfrac {5\ pi} {3}\) ">1 | \ (\ dfrac {7\ pi} {4}\) ">1 | \ (\ dfrac {11\ pi} {6}\) ">1 | \ (2\ pi\) ">1 |
Así que las soluciones únicas están en\(\theta =\dfrac{\pi }{3}, \dfrac{4\pi }{3}\). También hay dos soluciones repetidas en este set (¿las puedes encontrar?).
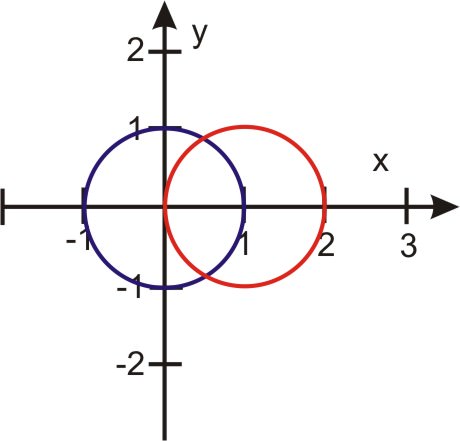
Aquí hay una gráfica que muestra las dos soluciones:
Revisar
Las gráficas de\(r=1\) y\(r=2\cos \theta \) se muestran a continuación.
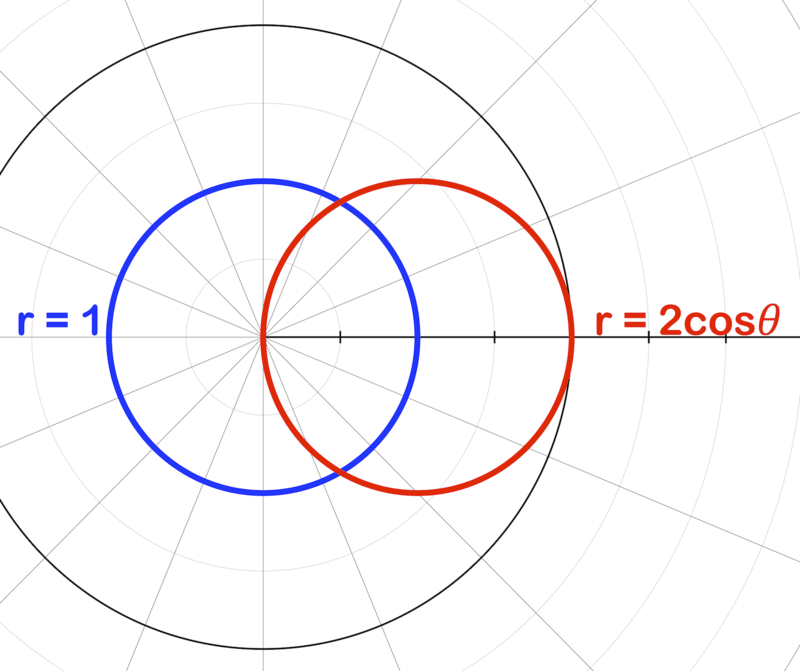
- ¿Cuántas veces se cruzan?
- ¿En qué cuadrantes se cruzan?
- ¿En qué puntos ocurren las intersecciones?
Basado en la imagen de abajo y la siguiente información: la intersección de las gráficas de\(r=\cos \theta \) y\(r=1−\cos \theta\)
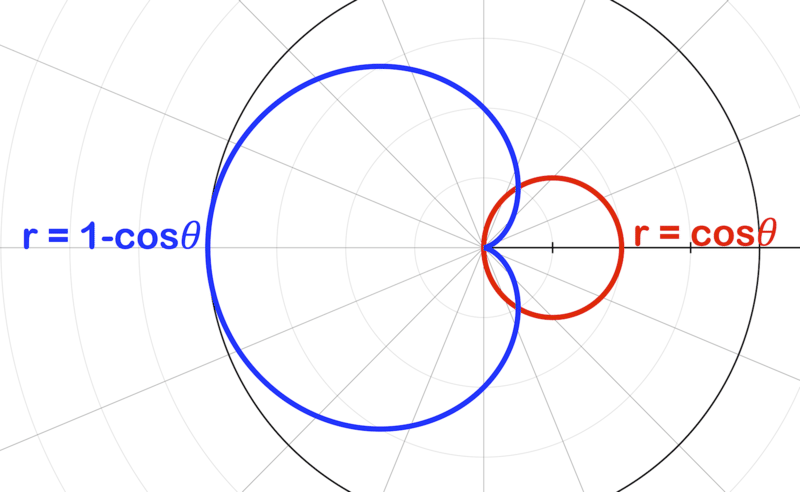
- ¿Identificar cuántas veces se cruzan?
- ¿En qué puntos ocurren las intersecciones?
Encuentra los puntos de intersección de los siguientes pares de curvas.
- \(r=2 ; r=2\cos \theta\)
- \(r=\sin 2\theta ; r=2\sin \theta\)
- \(r=2+2\sin \theta ; r=2−2\cos \theta\)
- \(r=3\cos \theta ; r=2−\cos \theta\)
Encuentra el (los) punto (s) de intersección para cada sistema de ecuaciones. Gráfica para verificar tu solución.
- \(r_1 =csc\theta ; r_2 =2\sin \theta\)
- \(r_1 =\cos \theta ; r_2 =1+\sin \theta\)
- \(r_1 =\sin \theta ; r_2 =\sin 2\theta\)
- \(r_1 =−4\sin \theta ; r_2 =−4\cos \theta\)
- \(r_1 =1−2\sin \theta ; r_2 =\sqrt{9 \cos (\theta )}\)
- \(r_1 =1−\cos \theta ; r_2 =4\cos (3\theta )\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.3.
El vocabulario
| Término | Definición |
|---|---|
| Cónico | Las secciones cónicas son aquellas curvas que se pueden crear por la intersección de un doble cono y un plano. Incluyen círculos, elipses, parábolas e hipérbolas. |
| Puntos de intersección | Los puntos de intersección son ubicaciones donde dos ecuaciones diferentes tienen las mismas soluciones. |
| coordenadas polares | Las coordenadas polares describen ubicaciones en una cuadrícula utilizando el sistema de coordenadas polares. La ubicación de cada punto está determinada por su distancia del polo y su ángulo con respecto al eje polar. |
| polo | El polo es el punto central de una gráfica polar. |
| cuadrante | Un cuadrante es un cuarto del plano de coordenadas. Los cuatro cuadrantes se numeran usando los números romanos I, II, III y IV, comenzando en la parte superior derecha y aumentando en sentido antihorario. |
Recursos adicionales
Video: Ejemplo: Encontrar puntos de intersección en una gráfica polar
Práctica: Sistemas de ecuaciones polares

