5.3.3: Fórmula Cuadrática y Sumas Complejas
- Page ID
- 107751
Resuelve ecuaciones cuadráticas con raíces complejas y suma y resta números complejos.
Raíces complejas de funciones cuadráticas
La función cuadrática\(y=x^2−2x+3\) (que se muestra a continuación) no interseca el eje x y por lo tanto no tiene raíces reales. ¿Cuáles son las complejas raíces de la función?
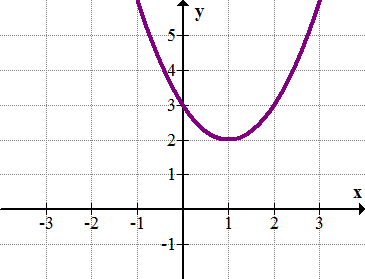
Raíces complejas de funciones cuadráticas
Recordemos que el número imaginario\(i\),, es un número cuyo cuadrado es —1:
\(\textcolor{red}{i^2=−1}\)y\(\textcolor{red}{i=\sqrt{−1}}\)
La suma de un número real y un número imaginario se llama un número complejo. Ejemplos de números complejos son\(5+4i\) y\(3−2i\). Todos los números complejos se pueden escribir en la forma a+bi donde a y b son números reales. Dos puntos importantes:
- El conjunto de números reales es un subconjunto del conjunto de números complejos donde\(b=0\). Ejemplos de números reales son 2,7,12, −4.2.
- El conjunto de números imaginarios es un subconjunto del conjunto de números complejos donde a=0. Ejemplos de números imaginarios son\(i\),\(−4i\),\(\sqrt{2}i\).
Esto significa que el conjunto de números complejos incluye números reales, números imaginarios y combinaciones de números reales e imaginarios.
Cuando una función cuadrática no interseca el eje x, tiene raíces complejas. Al resolver las raíces de una función algebraicamente usando la fórmula cuadrática, terminarás con un negativo bajo el símbolo de raíz cuadrada. Con tu conocimiento de los números complejos, aún puedes afirmar las raíces complejas de una función tal como lo harías decir las raíces reales de una función.
Vamos a resolver la ecuación cuadrática:\(m^2−2m+5=0\)
Puedes usar la fórmula cuadrática para resolver. Para esta ecuación cuadrática,\(a=1\),\(b=−2\),\(c=5\).
\ (\ begin {array} {l}
m=\ dfrac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\\
m=\ dfrac {- (\ textcolor {rojo} {-2})\ pm\ sqrt {(\ textcolor {rojo} {-2}) ^ {2} -4 (\ textcolor {rojo} {1}) (\ textcolor {rojo} {5})}} {2 (\ textcolor {rojo} {1})}\\
m=\ dfrac {2\ pm\ sqrt {4-20}} {2}\\
m=\ dfrac {2\ pm\ sqrt {-16}} {2}\ quad\ sqrt {-16} =\ sqrt {16}\ veces i=4 i\\
m=\ dfrac {2\ pm 4 i} {2}\
m=1\ pm 2 i\
m=1+2 i\ text {o} m=1-2 i
\ end {array}\)
No hay soluciones reales a la ecuación. Las soluciones a la ecuación cuadrática son\(1+2i\) y\(1−2i\).
Ahora, resolvamos la siguiente ecuación reescribiéndola como cuadrática y usando la fórmula cuadrática:
\(\dfrac{3}{e+3}−\dfrac{2}{e+2}=1\)
Para reescribir como una ecuación cuadrática, multiplica cada término por\((e+3)(e+2)\).
\(\begin{aligned} \dfrac{3}{e+3} \textcolor{red}{(e+3)(e+2)}−2e+2\textcolor{red}{(e+3)(e+2)}=1\textcolor{red}{(e+3)(e+2)} \\ 3(e+2)−2(e+3)=(e+3)(e+2) \end{aligned}\)
Ampliar y simplificar.
\(\begin{aligned} 3e+6−2e−6=e^2+2e+3e+6 \\ e^2+4e+6=0 \end{aligned}\)
Resuelve usando la fórmula cuadrática. Para esta ecuación cuadrática, a=1, b=4, c=6.
\ (\ begin {array} {l}
e=\ dfrac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\\
e=\ dfrac {- (\ textcolor {rojo} {4})\ pm\ sqrt {(\ textcolor {rojo} {4}) ^ {2} -4 (\ textcolor {rojo} {1}) (\ textcolor {rojo} {6})}} {2 (\ textcolor {rojo} {1})}\\
e=\ dfrac {-4\ pm\ sqrt {16-24}} {2}\
e=\ dfrac {-4\ pm\ sqrt {-8}} {2}\ quad\ sqrt {-8} =\ sqrt {8}\ veces i=\ sqrt {4\ cdot 2}\ veces i=2 i\ sqrt {2}\
e=\ dfrac {-4\ pm 2 i\ sqrt {2}} {2}\
e=-2\ pm i\ sqrt {2}\
e=-2+i\ sqrt {2}\ text {o} e=-2-i\ sqrt {2}
\ end {array}\)
No hay soluciones reales a la ecuación. Las soluciones a la ecuación son −2+i\ sqrt {2} y −2−i\ sqrt {2}
Finalmente, vamos a bosquejar la gráfica de la siguiente función cuadrática. ¿Cuáles son las raíces de esta función?
\(y=x^2−4x+5\)
Usa tu calculadora o una tabla para hacer un boceto de la función. Deberías obtener lo siguiente:
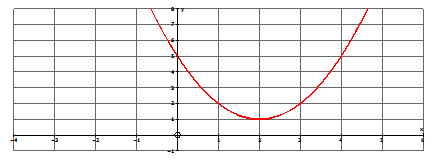
Como puede ver, la función cuadrática no tiene intercepciones x; por lo tanto, la función no tiene raíces reales. Para encontrar las raíces (que serán complejas), debes usar la fórmula cuadrática.
Para esta función cuadrática,\(a=1\),\(b=−4\),\(c=5\).
\ (\ begin {array} {l}
x=\ dfrac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\\
x=\ dfrac {- (\ textcolor {rojo} {-4})\ pm\ sqrt {(\ textcolor {rojo} {-4}) ^ {2} -4\ textcolor {rojo} {1}) (\ textcolor {rojo} {5})}} {2 (\ textcolor {rojo} {1})}\\
x=\ dfrac {4\ pm\ sqrt {16-20}} {2}\
x=\ dfrac {4\ pm\ sqrt {-4}} {2}\ quad\ sqrt {-4} =\ sqrt {4}\ veces i=2 i\
x=\ dfrac {4\ pm 2 i} {2}\\
x=2\ pm i\
x=2+i\ texto {o} x=2-i
\ end {array}\)
Las raíces complejas de la función cuadrática son 2+i y 2−i.
Antes, se le pidió que encontrara las complejas raíces de\(y=x^2−2x+3\).
Solución
Para encontrar las raíces complejas de la función\(y=x^2−2x+3\), se debe utilizar la fórmula cuadrática.
Para esta función cuadrática,\(a=1\),\(b=−2\),\(c=3\).
\ (\ begin {array} {l}
x=\ dfrac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\\
x=\ dfrac {- (\ textcolor {rojo} {-2})\ pm\ sqrt {(\ textcolor {rojo} {-2}) ^ {2} -4 (\ textcolor {rojo} {1}) (\ textcolor {rojo} {3})}} {2 (\ textcolor {rojo} {1})}\\
x=\ dfrac {2\ pm\ sqrt {4-12}} {2}\
x=\ dfrac {2\ pm\ sqrt {-8}} {2}\ quad\ sqrt {-8} =\ sqrt {8}\ veces i=2\ sqrt {2} i\
x=\ x=\ dfrac {2\ pm 2\ sqrt {2} i} {2}\
x=1\ pm\ sqrt {2} i
\ end {array}\)
Resuelve la siguiente ecuación cuadrática. Exprese todas las soluciones en forma radical más simple.
\(2n^2+n=−4\)
Solución
\(2n^2+n=−4\)
Establezca la ecuación igual a cero.
\(2n^2+n+4=0\)
Resuelve usando la fórmula cuadrática.
\ (\ begin {array} {l}
x=\ dfrac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\\
n=\ dfrac {- (\ textcolor {rojo} {1})\ pm\ sqrt {(\ textcolor {rojo} {1}) ^ {2} -4 (\ textcolor {rojo} {2}) (\ textcolor {rojo} {4})}} {2 (\ textcolor {rojo} {2})}\\
n=\ dfrac {-1\ pm\ sqrt {1-32}} {4}\
n=\ dfrac {-1\ pm\ sqrt {-31}} {4}\\
n=\ dfrac {-1\ pm i\ sqrt {31}} {4}
\ end {array}\)
Resuelve la siguiente ecuación cuadrática. Exprese todas las soluciones en forma radical más simple.
\(m^2+(m+1)^2+(m+2)^2=−1\)
Solución
\(m^2+(m+1)^2+(m+2)^2=−1\)
Ampliar y simplificar.
\(\begin{aligned} m^2+(m+1)(m+1)+(m+2)(m+2)&=−1 \\ m^2+m^2+m+m+1+m^2+2m+2m+4&=−1 \\ 3m^2+6m+5&=−1 \end{aligned}\)
Escribe la ecuación en forma general.
\(3m^2+6m+6=0\)
Dividir por 3 para simplificar la ecuación.
\(\begin{aligned} \dfrac{3m^2}{\textcolor{red}{3}}+\dfrac{6m}{\textcolor{red}{3}}+\dfrac{6}{\textcolor{red}{3}}&=\dfrac{0}{\textcolor{red}{3}} \\ m^2+2m+2&=0 \end{aligned}\)
Resuelve usando la fórmula cuadrática:
\ (\ begin {array} {l}
m=\ dfrac {-b\ pm\ sqrt {b^ {2} -4 a c}} {2 a}\\
m=\ dfrac {- (\ textcolor {rojo} {2})\ pm\ sqrt {(\ textcolor {rojo} {2}) ^ {2} -4 (\ textcolor {rojo} {1}) (\ textcolor {rojo} {2})}} {2 (\ textcolor {rojo} {1})}\\
m=\ dfrac {-2\ pm\ sqrt {4-8}} {2}\\
m=\ dfrac {-2\ pm\ sqrt {-4}} {2}\\
m=\ dfrac {-2\ pm 2 i} {2}\\
m=-1\ pm i
\ end {array}\)
¿Es posible que una función cuadrática tenga exactamente una raíz compleja?
Solución
No, incluso en polinomios de mayor grado, las raíces complejas siempre vendrán en parejas. Considera cuando usas la fórmula cuadrática— si tienes un negativo bajo el símbolo de raíz cuadrada, tanto la versión + como la versión - de las dos respuestas terminarán siendo complejas.
Revisar
- Si una función cuadrática tiene 2 intercepciones x, ¿cuántas raíces complejas tiene? Explicar.
- Si una función cuadrática no tiene intercepciones x, ¿cuántas raíces complejas tiene? Explicar.
- Si una función cuadrática tiene 1 intercepción x, ¿cuántas raíces complejas tiene? Explicar.
- Si quieres saber si una función tiene raíces complejas, ¿en qué parte de la fórmula cuadrática es importante enfocarse?
- Resuelve una ecuación cuadrática y obtienes 2 soluciones complejas. ¿Cómo puedes consultar tus soluciones?
- En general, se puede intentar resolver una ecuación cuadrática graficando, factorizando, completando el cuadrado o usando la fórmula cuadrática. Si una ecuación cuadrática tiene soluciones complejas, ¿qué métodos tiene para resolver la ecuación?
Resuelve las siguientes ecuaciones cuadráticas. Exprese todas las soluciones en forma radical más simple.
- \(x^2+x+1=0\)
- \(5y^2−8y=−6\)
- \(2m^2−12m+19=0\)
- \(−3x^2−2x=2\)
- \(2x^2+4x=−11\)
- \(−x^2+x−23=0\)
- \(−3x^2+2x=14\)
- \(x^2+5=−x\)
- \(\dfrac{1}{2}d^2+4d=−12\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 9.7.
El vocabulario
| Término | Definición |
|---|---|
| número complejo | Un número complejo es la suma de un número real y un número imaginario, escritos en la forma\(a+bi\). |
| raíz compleja | Una raíz compleja es un número complejo que, cuando se usa como valor input (\(x\)) de una función, da como resultado un valor output (\(y\)) de cero. |
| Números imaginarios | Un número imaginario es un número que puede escribirse como producto de un número real e i. |
| Fórmula cuadrática | La fórmula cuadrática establece que para cualquier ecuación cuadrática en la forma\(ax^2+bx+c=0\),\(x=\dfrac{−b\pm \sqrt{b^2−4ac}}{2a}\). |
| Número Real | Un número real es un número que se puede trazar en una recta numérica. Los números reales incluyen todos los números racionales e irracionales. |
Recursos adicionales
Video: Uso de la Fórmula Cuadrática
Práctica: Fórmula cuadrática y sumas complejas

