5.3.6: Forma trigonométrica de números complejos

Última actualización
Guardar como PDF

Page ID: 107762

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

x más y veces i es igual a r veces la suma de coseno theta e i veces seno theta.

Ya sabes cómo representar números complejos en el plano complejo usando coordenadas rectangulares y ya sabes cómo multiplicar y dividir números complejos. Representar estos puntos y realizar estas operaciones usando forma polar trigonométrica hará que sus cálculos sean más eficientes.

¿Cuáles son las dos formas de multiplicar los siguientes números complejos?

\((1+\sqrt{3}i)(\sqrt{2}−\sqrt{2}i)\)

Forma polar trigonométrica de números complejos

Cualquier punto representado en el plano complejo como se\(a+bi\) puede representar en forma polar al igual que cualquier punto en el sistema de coordenadas rectangulares. La forma polar trigonométrica de un número complejo describe la ubicación de un punto en el plano complejo usando el ángulo y el radio del punto. Utilizarás la distancia desde el punto hasta el origen como r y el ángulo que hace el punto como\(\theta \).

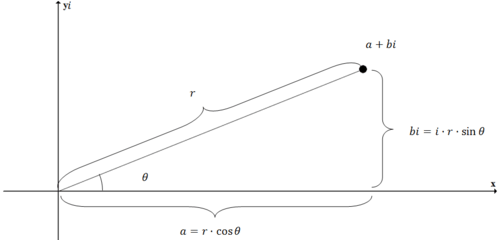
Como puede ver, el punto a+bi también se puede representar como\(r\cdot \cos \theta +i\cdot r\cdot \sin \theta \). La forma polar trigonométrica se puede abreviar factorizando la r y anotando las primeras letras:

\(r(\cos \theta +i\cdot \sin \theta )\rightarrow r\cdot \; cis \; \theta\)

La abreviatura\(r\cdot \; cis \; \theta \) se lee como “\(r\)beso theta”. Permite representar un punto como radio y ángulo.

Tome el siguiente número complejo en forma rectangular.

\(1−\sqrt{3}i\)

Para convertir el siguiente número complejo de forma rectangular a forma polar trigonométrica, busque el radio usando el valor absoluto del número.

\(r^2 =1^2+(−\sqrt{3})^2\rightarrow r=2\)

El ángulo se puede encontrar con trigonometría básica y el conocimiento de que el lado opuesto es siempre el componente imaginario y el lado adyacente es siempre el componente real.

\(\tan \theta =−\dfrac{\sqrt{3}}{1} \rightarrow \theta =60^{\circ}\)

Así es la forma trigonométrica\(2 \; cis \; 60^{\circ} \).

Un gran beneficio de la forma cis es que hace que multiplicar y dividir números complejos sea extremadamente fácil. Por ejemplo:

Dejar:\(z_1 =r_1 \cdot \; cis \; \theta_1 ,z_2 =r_2 \cdot \; cis \; \theta_2\) con\(r_2 \neq 0\).

Entonces:

\(\begin{aligned} z_1 \cdot z_2 &=r_1 \cdot r_2 \cdot \; cis \; (\theta_1 +\theta_2) \\ z_1 \div z_2 &=\dfrac{r_1 }{r_2} \cdot \; cis \;(\theta_1 −\theta_2) \end{aligned}\)

Para problemas básicos, la cantidad de trabajo requerido para computar productos y cocientes para números complejos dados en cualquiera de las formas es aproximadamente equivalente. Para preguntas más desafiantes, la forma polar trigonométrica se vuelve significativamente ventajosa.

Ejemplo\(\PageIndex{1}\)

Anteriormente, se le preguntó cómo multiplicar los números complejos\((1+\sqrt{3}i)(\sqrt{2}−\sqrt{2}i)\).

Solución

En coordenadas rectangulares:

\((1+\sqrt{3}i)(\sqrt{2}−\sqrt{2}i)=\sqrt{2}−\sqrt{2}i+\sqrt{6} i+\sqrt{6}\)

En coordenadas polares trigonométricas,\(1+\sqrt{3}i=2 \; cis \; 60^{\circ} \) y\(\sqrt{2}−\sqrt{2}i=2 \; cis \;−45^{\circ} \). Por lo tanto:

\((1+\sqrt{3}i)(\sqrt{2}−\sqrt{2}i)=2 \; cis \; 60^{\circ} \cdot 2 \; cis \;−45^{\circ} =4 \; cis \; 105^{\circ}\)

Ejemplo\(\PageIndex{2}\)

Convierta el siguiente número complejo de forma polar trigonométrica a forma rectangular.

\(4 \; cis \;(3\dfrac{\pi}{4})\)

Solución

\(4 \; cis \; \left(3\dfrac{\pi}{4}\right)=4\left(\cos \left(\dfrac{3 \pi}{4}\right)+i\cdot \sin \left(\dfrac{3 \pi}{4}\right)\right)=4\left(−\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}i\right)=−2\sqrt{2}+2\sqrt{2}i\)

Ejemplo\(\PageIndex{3}\)

Divide los siguientes números complejos.

\(\dfrac{4 \; cis \; 32^{\circ} }{2 \; cis \; 2^{\circ}}\)

Solución

\(\dfrac{4 \; cis \; 32^{\circ} }{2 \; cis \; 2^{\circ} }=42 \; cis \; (32^{\circ} −2^{\circ} )=2 \; cis \; (30^{\circ} )\)

Ejemplo\(\PageIndex{4}\)

Traduzca el siguiente número complejo de forma rectangular a forma polar trigonométrica:

Solución

\(8=8 \; cis \; 0^{\circ}\)

Tenga en cuenta que esta no tiene parte compleja y por lo tanto no tiene ángulo.

Ejemplo\(\PageIndex{5}\)

Multiplique los siguientes números complejos en forma polar trigonométrica.

\(4 \; cis \; 34^{\circ} \cdot 5 \; cis \; 16^{\circ} \cdot \dfrac{1}{2} \; cis \; 100^{\circ}\)

Solución

\(\begin{aligned} 4 \; cis \; 34^{\circ} \cdot 5 \; cis \; 16^{\circ} \cdot \dfrac{1}{2} \; cis \; 100^{\circ} \\ &=4\cdot 5\cdot 12\cdot \; cis \; (34^{\circ} +16^{\circ} +100^{\circ} ) \\ &=10 \; cis \; 150 \end{aligned}\)

Tenga en cuenta lo fácil que es hacer productos y cocientes en forma polar trigonométrica.

Revisar

Traduzca los siguientes números complejos de forma polar trigonométrica a forma rectangular.

1. \(5 \; cis \; 270^{\circ}\)

2. \(2 \; cis \; 30^{\circ}\)

3. \(−4 \; cis \; \dfrac{\pi}{4}\)

4. \(6 \; cis \; \dfrac{\pi}{3}\)

5. \(2 \; cis \; \dfrac{5\pi}{2}\)

Traduzca los siguientes números complejos de forma rectangular a forma polar trigonométrica.

6. \(2−i\)

7. \(5+12i\)

8. \(6i+8\)

9. \(i\)

Complete los siguientes cálculos y simplifique.

10. \(2 \; cis \; 22^{\circ} \cdot \dfrac{1}{5} \; cis \; 15^{\circ} \cdot 3 \; cis \; 95^{\circ}\)

11. \(9 \; cis \; 98^{\circ} \div 3 \; cis \; 12^{\circ}\)

12. \(15 \; cis \; \dfrac{\pi}{4}\cdot 2 \; cis \; \dfrac{\pi}{6}\)

13. \(−2 \; cis \; \dfrac{2\pi}{3}\div 15 \; cis \; \dfrac{7 \pi}{6}\)

Dejar\(z_1 =r_1 \cdot \; cis \; \theta_1 \) y\(z_2 =r_2 \cdot \; cis \; \theta_2\) con r_2\ neq 0\).

14. Utilizar las identidades trigonométricas de suma y diferencia para probarlo\(z_1 \cdot z_2 =r_1 \cdot r_2 \cdot \; cis \; (\theta_1 +\theta_2)\).

15. Utilizar las identidades trigonométricas de suma y diferencia para probarlo\(z_1 \div z_2 =r_1 r_2 \cdot \; cis \; (\theta_1 −\theta_2)\).

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 11.3.

El vocabulario

Término	Definición
\(r\; cis \;\theta\)	\(r\; cis \;\theta \)es la abreviatura de la expresión\(r\cos \theta +ri\sin \theta \).
plano complejo	El plano complejo es la representación gráfica del conjunto de todos los números complejos.
forma polar	La forma polar de un punto o una curva se da en términos de r y\(\theta \) y se grafica en el plano polar.
forma rectangular	La forma rectangular de un punto o una curva se da en términos de x e y y se grafica en el plano cartesiano.
forma trigonométrica	Escribir un número complejo en forma trigonométrica significa escribirlo en el formulario\(r\cos \theta +ri\sin \theta \). \(r\; cis \;\theta \)es la abreviatura de esta expresión.
forma polar trigonométrica	Escribir un número complejo en forma trigonométrica significa escribirlo en el formulario\(r\cos \theta +ri\sin \theta \). \(r\; cis \;\theta \)es la abreviatura de esta expresión.

Recursos adicionales

Elemento Interactivo

Video: Números complejos en forma trigonométrica

Práctica: Forma trigonométrica de números complejos

Mundo real: mantenerse al día