5.3.8: Geometría de Raíces Complejas

Raíces igualmente espaciadas alrededor de círculos.

Acabas de terminar un problema donde necesitabas resolver la ecuación:

\(x^4=16\)

Después de resolver por las raíces, que fueron\(2,\; −2,\; 2i,\; −2i\) tu instructor te pide que las trazar en el plano complejo.

¿Puedes lograrlo?

Siempre es bueno tener una idea intuitiva de los valores trazándolos. Esta tendencia se extiende también a los números complejos.

Las cinco raíces de la ecuación\(x^5−32=0\) involucran una raíz real y cuatro complejas. Echemos un vistazo a una trama de estas raíces en el plano complejo.

Figura\(\PageIndex{1}\)

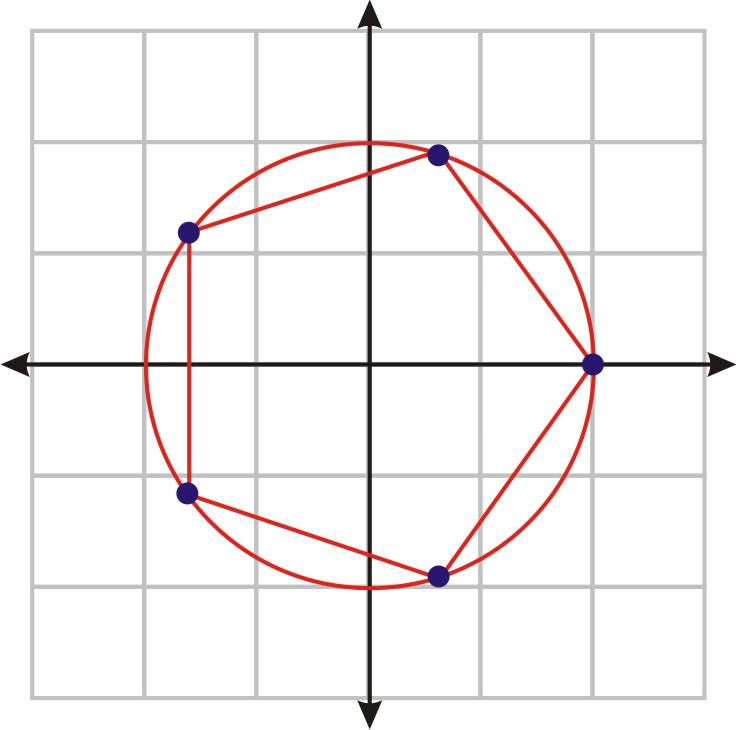
Las\(n^{th}\) raíces de un número complejo, cuando se grafican en el plano complejo, están igualmente espaciadas alrededor de un círculo. Entonces, en lugar de tener todas las raíces, todo lo que se necesita para graficar las raíces es una de ellas y el radio del círculo. Para este ejemplo en particular, las raíces son\(\dfrac{2\pi }{5}\) o\(72^{\circ} \) separadas. Esto va de la mano con lo que sabemos de los pentágonos regulares. Las raíces están separadas por\(\dfrac{2\pi }{n}\) grados.

Echemos un vistazo a algunos problemas que involucran la geometría de raíces complejas.

1. Calcular las dos raíces para\(x^2=1\) y representarlas gráficamente.

\ (\ begin {alineado}
x^ {2} =1 &\\
r &=\ sqrt {x^ {2} +y^ {2}}\\
r &=\ r &=\ sqrt {(1) ^ {2} + (0) ^ {2}}\\
r &=1\\
&\ theta=\ tan ^ {-1}\ izquierda (\ frac {0} {1}\ derecha) =0
\ fin {alineado}\)

Escribe una expresión para determinar las dos raíces de\(1=1+0i\)

\ (\ begin {alineado}
1^ {1/2} &=\ izquierda [1 (\ cos (0+2\ pi k) +i\ sin (0+2\ pi k)\ derecha] ^ {1/2}\\
&=1\ izquierda (\ cos\ frac {2\ pi k} {2} +i\ sin\ frac {2\ pi k} {2}\ derecha) k=0,1\
x_ {1} &=1\ izquierda (\ cos\ frac {0} {2} +i\ sin\ frac {0} {2}\ derecha)\ fila derecha 1 (\ cos 0+i\ sin 0) =1\ quad \ text {for} k=0\\
x_ {2} &=1\ left (\ cos\ frac {2\ pi} {2} +i\ sin\ frac {2\ pi} {2}\ derecha) =-1\ quad\ texto {para} k=1
\ end {alineado}\)

Estas raíces se trazan aquí:

Figura\(\PageIndex{2}\)

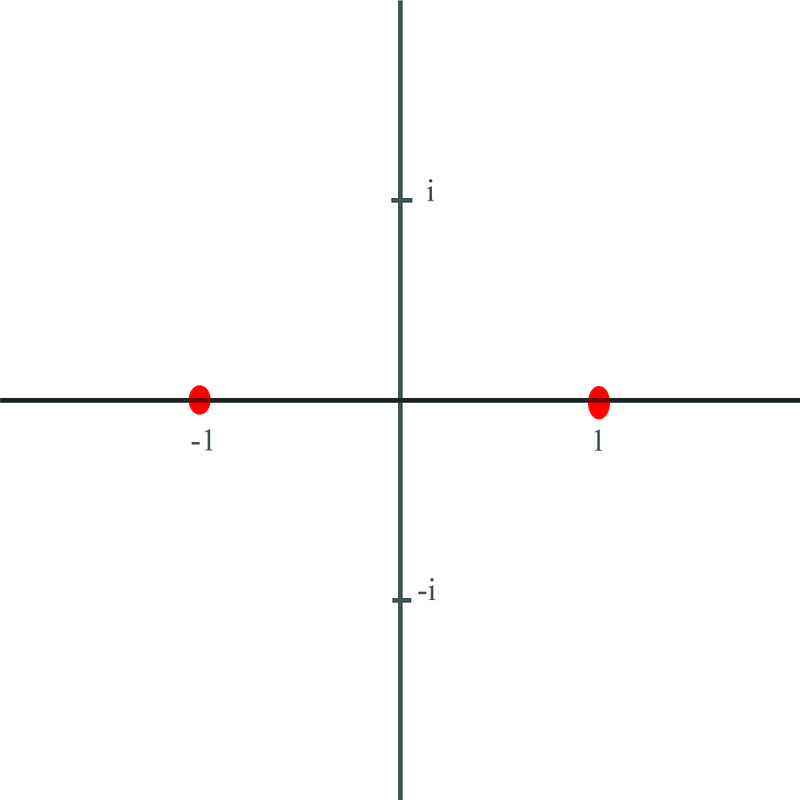
2. Calcular las tres raíces para\(x^3=1\) y representarlas gráficamente.

En forma estándar,\(1=1+0i r=1\) y\(\theta =0\). La forma polar es\(1+0i=1[\cos(0+2\pi k)+i\sin(0+2\pi k)]\). La expresión para determinar las raíces cubicas de 1+0i es:

\((1+0i)^{1/3}=1^{1/3}\left(\cos \dfrac{0+2\pi k}{3}+i \sin \dfrac{0+2\pi k}{3}\right)\)

Cuando\(k=0\),\(k=1\) y\(k=2\) las tres raíces cúbicas de 1 son\(1,\; −\dfrac{1}{2}+i\dfrac{\sqrt{3}}{2},\;−\dfrac{1}{2}−i\dfrac{\sqrt{3}}{2}\). Cuando estas tres raíces se representan gráficamente, los tres puntos, en el círculo con un radio de 1 (la raíz cúbica de 1 es 1), forman un triángulo.

Figura\(\PageIndex{3}\)

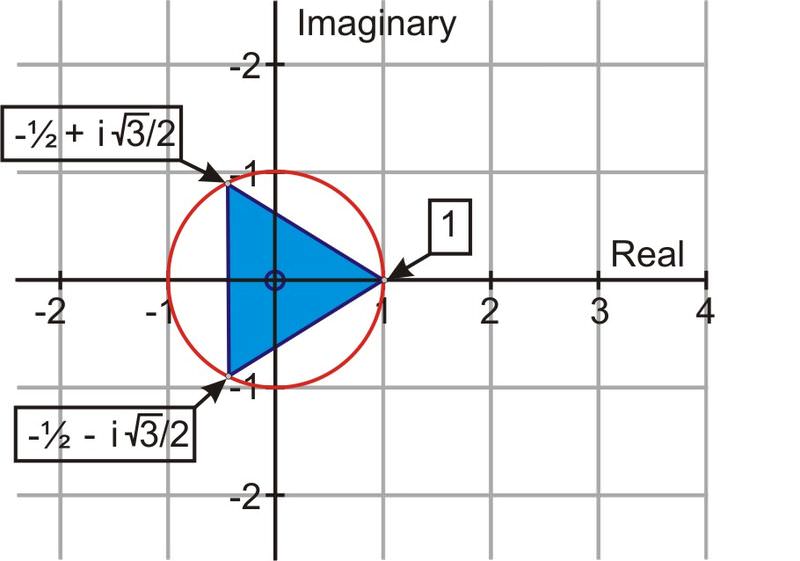
3. Calcular las cuatro raíces para\(x^4=1\) y representarlas gráficamente

\ (\ begin {alineado}
x^ {4} &=1\\
r &=\ sqrt {x^ {2} +y^ {2}}\\
r &=\ r &=\ sqrt {(1) ^ {2} + (0) ^ {2}}\\
r &=1\\
&\ theta=\ tan ^ {-1}\ izquierda (\ frac {0} {1}\ derecha) =0
\ fin {alineado}\)

Escribe una expresión para determinar las raíces cubas de\(1=1+0i\)

\ (\ begin {array} {rlr}
1^ {\ frac {1} {4}} & =\ left [1 (\ cos (0+2\ pi k) +i\ sin (0+2\ pi k)\ derecha] ^ {1/4} &\\
& =1\ izquierda (\ cos\ frac {2\ pi k} {4} +i\ sin\ frac {2\ pi k} 4}\ derecha) k=0,1,2,3 &\\
x_ {1} & =1\ izquierda (\ cos\ frac {0} {4} +i\ sin\ frac {0} {4}\ derecha)\ fila derecha 3 (\ cos 0+i\ sin 0) =1 & &\ text {para} k=0\\
x_ {2} & =1\ izquierda (\ cos\ frac {2\ pi} {4} +i\ sin\ frac {2\ pi} {4}\ derecha) =0+i=i & &\ text {para} k=1\
x_ {3} y =1 izquierda\ (\ cos\ frac {4\ pi} {4} +i\ sin\ frac {4\ pi} {4}\ derecha) =-1-0 i=-1 & &\ text {para} k= 2\\
x_ {4} & =1\ izquierda (\ cos\ frac {6\ pi} {4} +i\ sin\ frac {6\ pi} {4}\ derecha) =0-i=-i &\ text {para} k=3
\ end {array}\)

Estas raíces se trazan aquí:

Figura\(\PageIndex{4}\)

Ejemplo\(\PageIndex{1}\)

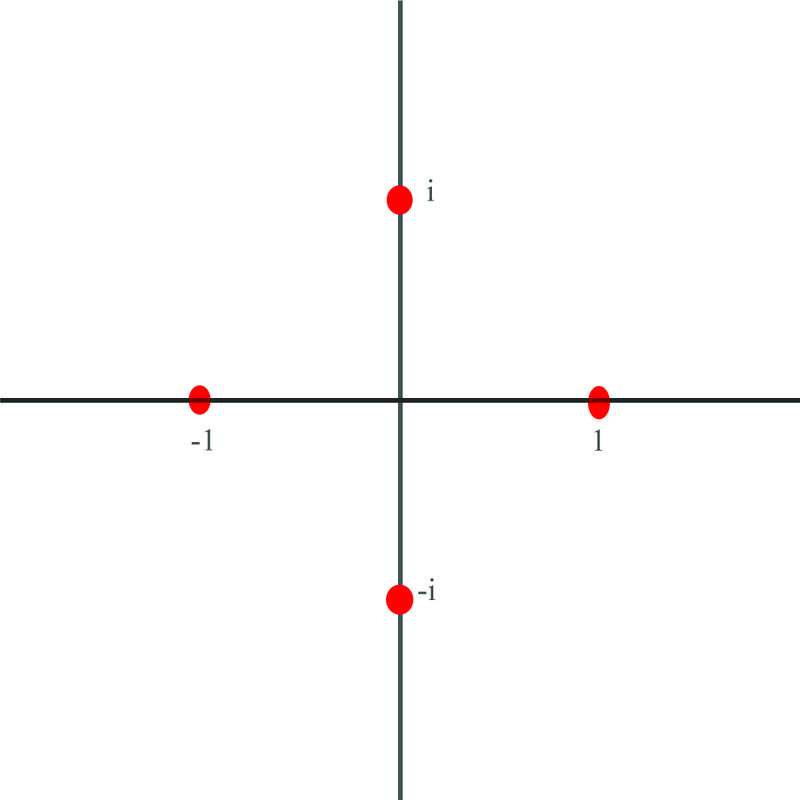
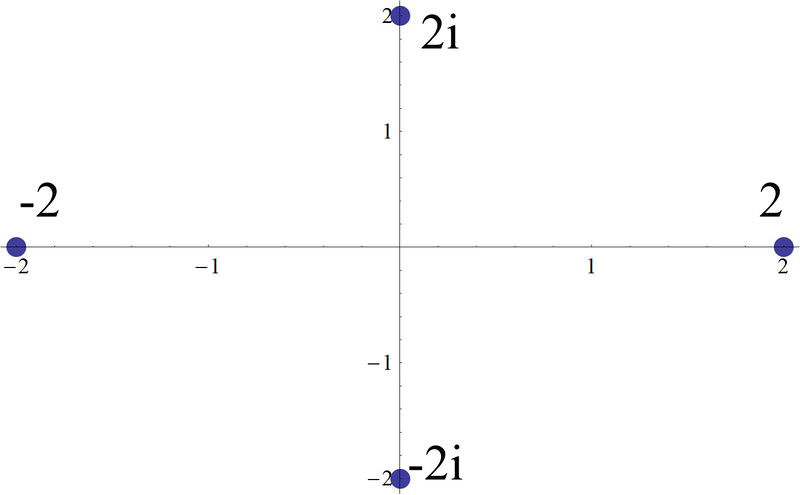
Antes, se le pidió que conspirara\(2,\;−2,\;2i,\;−2i\) en un avión.

Solución

Se puede ver una trama de estas raíces aquí. Observe, como se mencionó anteriormente, que las raíces se colocan equidistantes alrededor de un círculo que podría dibujarse en el plano con un radio de dos.

Figura\(\PageIndex{5}\)

Ejemplo\(\PageIndex{2}\)

En los ejemplos anteriores, viste las raíces complejas determinadas para una serie de diferentes órdenes polinomiales, como\(x^2,\; x^3,\; x^4\). ¿Qué conclusión se puede sacar sobre el número de raíces complejas que existen en relación con el orden del polinomio que se está resolviendo?

Solución

Se puede concluir que el número total de raíces es el mismo que el orden del polinomio en consideración. Por ejemplo,\(x^2\) tendrá 2 raíces, mientras que\(x^3\) tendrá 3 raíces, etc.

Ejemplo\(\PageIndex{3}\)

¿Cuál es el espaciado en coordenadas polares entre las raíces del polinomio\(x^6=12\)?

Solución

Dado que hay seis raíces totales, y todas las raíces están igualmente espaciadas alrededor de un círculo en el plano complejo, hay\(\dfrac{360^{\circ} }{6}=60^{\circ} \) entre raíces.

Ejemplo\(\PageIndex{4}\)

Resolver por las raíces de la ecuación\(x^2−3x+5=0\) y trazarlas.

Solución

Esta ecuación se puede resolver usando la fórmula cuadrática familiar. Observe que anteriormente usábamos cuadráticas que daban soluciones reales. Sin embargo, no hay razón para limitar el conjunto de soluciones a los números reales, ahora que también sabe cómo utilizar números complejos.

\ (\ begin {alineado}
x&=\ frac {- (-3)\ pm\ sqrt {(-3) ^ {2} - (4) (1) (5)}} {(2) (1)}\\
&=\ frac {3\ pm\ sqrt {-11}} {2}\\
&=\ frac {3\ pm i\ sqrt {11}} {2}}\\
&=\ frac {3} {2}\ pm\ frac {i\ sqrt {11}} {2}
\ end {alineado}\)

Una trama de estas raíces se ve así:

Figura\(\PageIndex{6}\)

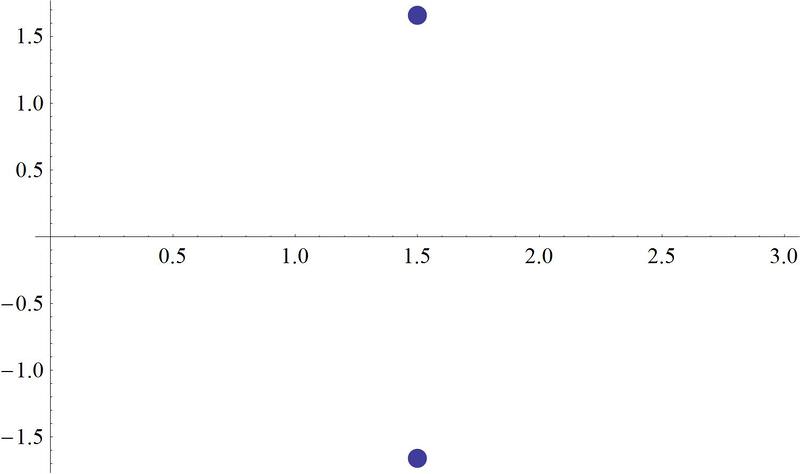
donde el eje vertical es la línea numérica imaginaria.

Revisar

1. ¿Cuántas raíces\(x^5=1\) tiene?
2. Calcular las raíces de\(x^5=1\) y representarlas gráficamente.
3. ¿Cuántas raíces\(x^8=1\) tiene?
4. Calcular las raíces de\(x^8=1\) y representarlas gráficamente.
5. ¿Cuántas raíces\(x^{10}=1\) tiene?
6. Calcular las raíces de\(x^{10}=1\) y representarlas gráficamente.
7. ¿Cuántas raíces\(x^4=16\) tiene?
8. Calcular las raíces de\(x^4=16\) y representarlas gráficamente.
9. ¿Cuántas raíces\(x^3=27\) tiene?
10. Calcular las raíces de\(x^3=27\) y representarlas gráficamente.
11. ¿Cómo se\(x^3=−1\) comparan las soluciones de la ecuación con las soluciones de la ecuación\(x^3=1\)?
12. Describir cómo representar las raíces de\(x^6=1\) gráficamente sin resolver primero la ecuación.
13. Describir cómo representar las raíces de\(x^{12}=1\) gráficamente sin resolver primero la ecuación.
14. Describir cómo representar las raíces de\(x^4=81\) gráficamente sin resolver primero la ecuación.
15. Describir cómo representar las raíces de\(x^8=256\) gráficamente sin resolver primero la ecuación.

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.15.

Recursos adicionales

Video: Determinar las enésimas raíces de un número complejo