5.3.10: Teorema de Demoivre y enésima Raíces

Última actualización
Guardar como PDF

Page ID: 107772

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Elevar números complejos a los poderes o encontrar sus raíces.

Ya sabes cómo multiplicar dos números complejos juntos y has visto las ventajas de usar la forma polar trigonométrica, especialmente al multiplicar más de dos números complejos al mismo tiempo. Debido a que elevar un número a una potencia de número entero es multiplicación repetida, también se sabe cómo elevar un número complejo a una potencia numérica entera.

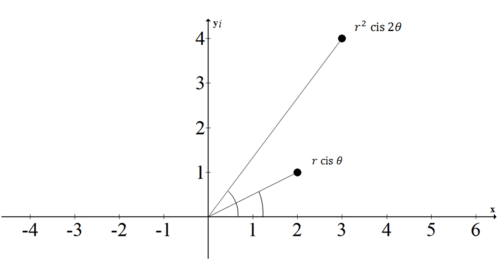
¿Qué es una interpretación geométrica de la cuadratura de un número complejo?

Recordemos que si\(z_1=r_1\cdot \; cis \; \theta_1\) y\(z_2=r_2\cdot \; cis \; \theta_2\) con\(r_2\neq 0\), entonces\(z_1\cdot z_2=r_1\cdot r_2\cdot \; cis \; (\theta 1+\theta 2)\).

Si\(z_1=z_2=z=r \; cis \; \theta \) entonces puedes determinar\(z_2\) y\(z_3\):

\(\begin{aligned} z^2 &=r\cdot r\cdot \; cis \; (\theta +\theta ) =r^2 \; cis \; (2\cdot \theta )\\ z^3&=r^3 \; cis \; (3\cdot \theta ) \end{aligned}\)

El teorema de De Moivre simplemente generaliza este patrón al poder de cualquier entero positivo.

\(z^n=r^n\cdot \; cis \; (n\cdot \theta )\)

Además de elevar un número complejo a una potencia, también puedes tomar raíces cuadradas, raíces cubicas y\(n^{th}\) raíces de números complejos. Supongamos que tienes un número complejo\(z=r \; cis \; \theta \) y quieres tomar la\(n^{th}\) raíz de z. En otras palabras, quieres encontrar un número\(v=s\cdot \; cis \; \beta \) tal que\(v^n=z\). Hacer alguna sustitución y manipulación:

\(\begin{aligned} v^n&=z \\ (s\cdot \; cis \; \beta )^n&=r\cdot \; cis \; \theta \\ s^n \cdot \; cis \; (n\cdot \beta )&=r\cdot \; cis \; \theta \end{aligned}\)

Se puede ver en este punto que para encontrar s se necesita tomar la\(n^{th}\) raíz de r. la parte más complicada es encontrar los ángulos, porque\(n\cdot \beta \) podría ser cualquier ángulo coterminal con\(\theta \). Esto significa que existen\(n\) diferentes\(n^{th}\) raíces de\(z\).

\(\begin{aligned} n\cdot \beta &=\theta +2\pi k\\ \beta &=\dfrac{\theta +2\pi k}{n} \end{aligned}\)

El número\(k\) puede ser todos los números de conteo incluyendo ceros hasta\(n−1\). Entonces si estás tomando la 4ta raíz, entonces\(k=0,1,2,3\).

Así, la\(n^{th}\) raíz de un número complejo requiere n cálculos diferentes, uno para cada raíz:

\(v=\sqrt{n}{r} \cdot \; cis \; \left(\dfrac{\theta +2\pi k}{n}\right)\)para\({k \in I | 0\leq k\leq n−1}\)

Para aplicar esta fórmula, encuentra la raíz cubo del número 8. La mayoría de los estudiantes saben que 23=8 y así saben que 2 es la raíz cubo de 8. Sin embargo, no se dan cuenta de que hay otras dos raíces cubicas que son mis\ sin g. Recuerda escribir\(k=0,1,2\) y usar el círculo unitario siempre que sea posible para ayudarte a encontrar las tres raíces cubicas.

\ (\ begin {aligned}
8 &=8\ nombreoperador {cis} 0 =( s\ cdot\ nombreoperador {cis}\ beta) ^ {3}\\
z_ {1} &=2\ cdot\ nombreoperador {cis}\ left (\ frac {0+2\ pi\ cdot 0} {3}\ derecha) =2\ nombreoperador {cis} 0=2 (\ cos 0+i\ cdot\ sin 0) =2 (1+0) =2\\
z_ {2} &=2\ cdot\ nombreoperador {cis}\ izquierda (\ frac {0+2\ pi\ cdot 1} {3}\ derecha) =2\ nombreoperador {cis}\ izquierda (\ frac {2\ pi} {3}\ derecha)\\
&=2\ izquierda (\ cos\ izquierda (\ frac {2\ pi} {3}\ derecha) +i\ cdot\ sin\ izquierda (\ frac {2\ pi} {3}}\ derecha)\ derecha) =2\ izquierda (-\ frac {1} {2} +\ frac {\ sqrt {3}} {2} i\ derecha) =-1+i\ sqrt {3}\\
z_ {3} &=2\ cdot\ nombreoperador {cis}\ izquierda (\ frac {0+2\ pi\ cdot 2} {3}\ derecha) =2\ nombreoperador {cis}\ izquierda (\ frac {4\ pi} {3}\ derecha)\\
&=2\ izquierda (\ cos\ izquierda (\ frac {4\ pi} {3}\ derecha) +i\ cdot\ sin\ izquierda (\ frac {4\ pi} {3}\ derecha)\ derecha) =2\ izquierda (-\ frac {1} {2} -\ frac {\ sqrt {3}} {2} i\ derecha) =-1-i\ sqrt {3}
\ end {alineado}\)

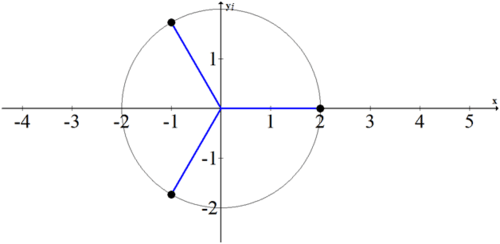
Las raíces cubicas de 8 son 2,\(−1+i\sqrt{3} \),\(−1−i\sqrt{3} \).

Para comprobar, que son las raíces cubicas, las cubos todas simplifican.

\(\begin{aligned} z^3_1 &=2^3=8\\ z^3_2&=(−1+i\sqrt{3} )^3 \\ &=(−1+i\sqrt{3} )\cdot (−1+i\sqrt{3} )\cdot (−1+i\sqrt{3} )\\ &=(1−2i\sqrt{3} −3)\cdot (−1+i\sqrt{3} ) \\ &=(−2−2i\sqrt{3} )\cdot (−1+i\sqrt{3} ) \\ &=2−2i\sqrt{3} +2i\sqrt{3} +6 \\&=8\end{aligned}\)

Tenga en cuenta cuántos pasos y oportunidades hay para cometer un error al multiplicar múltiples términos en forma rectangular. Cuando compruebes z3, usa forma polar trigonométrica.

\(\begin{aligned} z^3_3&=2^3 \; cis \; \left(3\cdot \dfrac{4\pi }{3}\right) \\ &=8(\cos 4\pi +i\cdot \sin 4\pi ) \\ &=8(1+0)\\&=8 \end{aligned}\)

Ejemplo\(\PageIndex{1}\)

Anteriormente, se le preguntó qué es una interpretación geométrica de cuadrar un número complejo. Al cuadrar un número complejo se produce un nuevo número complejo. El ángulo se duplica y la magnitud se cuadra, por lo que geométricamente se ve una rotación.

Solución

Ejemplo\(\PageIndex{2}\)

Traza gráficamente las raíces de 8 y discute cualquier patrón que notes.

Solución

Los tres puntos están igualmente espaciados alrededor de un círculo de radio 2. Sólo uno de los puntos,\(2+0i\), se compone únicamente de números reales. Los otros dos puntos tienen tanto un componente real como uno imaginario por lo que están fuera del eje x.

A medida que se sienta más cómodo con las raíces, solo puede determinar el número de puntos que deben espaciarse uniformemente alrededor de un cierto círculo de radio y encontrar el primer punto. El resto es solo lógica.

Ejemplo\(\PageIndex{3}\)

¿De qué son las cuartas raíces\(16 \; cis \; 48^{\circ} \)?

Solución

Habrá 4 puntos, cada uno\(90^{\circ} \) aparte con el primer punto en\(2 \; cis \; (12^{\circ} )\).

\(2 \; cis \; (12^{\circ} )\),\( 2 \; cis \; (102^{\circ} )\),\(2 \; cis \; (192^{\circ} )\),\(2 \; cis \; (282^{\circ} )\)

Ejemplo\(\PageIndex{4}\)

Resuelve para z encontrando la\(n^{th}\) raíz del número complejo.

\(z^3=64−64\sqrt{3}i\)

Solución

Primero escribe el número complejo en\(\; cis \;\) forma. Acuérdate de identificar\(k=0,1,2\). Esto significa que las raíces aparecerán cada una\(\sqrt{360^{\circ} }{3}=120^{\circ} \).

\(\begin{aligned} z^3 &=64−64\sqrt{3}i =128\cdot \; cis \; 300^{\circ} \\ z_1&=128^{\dfrac{1}{3}} \cdot \; cis \; \left(\dfrac{300}{3}\right)^{\circ} =128^{\dfrac{1}{3}} \cdot \; cis \; \left(\dfrac{300}{3}\right)^{\circ} \\ z_2 &=128^{\dfrac{1}{3}} \cdot \; cis \; (220^{\circ} )\\ z_3 &=128^{\dfrac{1}{3}} \cdot \; cis \; (340^{\circ} ) \end{aligned}\)

Ejemplo\(\PageIndex{5}\)

Utilice el Teorema de De Moivre para evaluar el siguiente poder.

\((\sqrt{2} −\sqrt{2} i)^6\)

Solución

Primero escribe el número en forma polar trigonométrica, luego aplica el Teorema de De Moivre y simplifica.

\(\begin{aligned} (\sqrt{2} −\sqrt{2} i)^6&=(2 \; cis \; 315^{\circ} )^6 \\ &=2^6\cdot \; cis \; (6\cdot 315^{\circ} ) \\ &=64\cdot \; cis \; (1890^{\circ} ) \\ &=64\cdot \; cis \; (1890^{\circ} )\\&=64\cdot \; cis \; (90^{\circ} ) \\&=64(\cos 90^{\circ} +i\cdot \sin 90^{\circ} ) \\&=64(0+i) \\&=64i \end{aligned}\)

Revisar

Utilice el Teorema de De Moivre para evaluar cada expresión. Escribe tus respuestas en forma rectangular.

1. \((1+i)^5\)

2. \((1−\sqrt{3}i)^3\)

3. \((1+2i)^6\)

4. \((\sqrt{3}−i)^5\)

5. \(\left(\dfrac{1}{2}+\dfrac{i\sqrt{3}}{2}\right)^4\)

6. Encuentra las raíces cubicas de\(3+4i\).

7. Encuentra las\(5^{th}\) raíces de\(32i\).

8. Encuentra las\(5^{th}\) raíces de\(1+\sqrt{5}i\).

9. Encuentra las\(6^{th}\) raíces de - 64 y trazarlas en el plano complejo.

10. Usa tus respuestas a #9 para ayudarte a resolver\(x^6+64=0\).

Para cada ecuación: a) indicar el número de raíces, b) calcular las raíces y c) representar gráficamente las raíces.

11. \(x^3=1\)

12. \(x^8=1\)

13. \(x^{12}=1\)

14. \(x^4=16\)

15. \(x^3=27\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 11.4.

El vocabulario

Término	Definición
\(n^{th}\)raíces de la unidad	Las\(n^{th}\) raíces de la unidad son las\(n^{th}\) raíces del número 1.
número complejo	Un número complejo es la suma de un número real y un número imaginario, escritos en la forma\(a+bi\).
plano complejo	El plano complejo es la representación gráfica del conjunto de todos los números complejos.
Teorema de De Moivre	El teorema de De Moivre es el único método manual práctico para identificar los poderes o raíces de los números complejos. El teorema afirma que si\(z=r(\\cos \theta +i\\sin \theta )\) es un número complejo en\(r\; cis \;\theta \) forma y n es un entero positivo, entonces\(z^n=r^n(\cos (n\theta )+i\sin (n\theta ))\).
forma polar trigonométrica	Escribir un número complejo en forma trigonométrica significa escribirlo en el formulario\(r\cos \theta +ri\sin \theta \). \(r\; cis \;\theta \)es la taquigrafía de esta expresión.

Recursos adicionales

Elemento Interactivo

Video: Determinar las\(n^{th}\) raíces de un número complejo

Práctica: Teorema y\(n^{th}\) raíces de Demoivre