14.3: Estimación del Modelo de Regresión con la Línea de Mínimos Cuadrados

Última actualización
Guardar como PDF

Page ID: 151927

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Ahora volvemos al caso donde conocemos los datos y podemos ver la correlación lineal en una gráfica de dispersión, pero no conocemos los valores de los parámetros del modelo subyacente. Los tres parámetros que desconocemos son el\(y\) ‐intercept\(\beta_{0}\), la pendiente (\(\beta_{1}\)) y la desviación estándar del error residual (\(\sigma\)):

Parámetro de pendiente:\(b_1\) será un estimador para\(\beta_{1}\)

Parámetro Y‐intercept:\(b_0\) será un estimador para\(\beta_{0}\)

Desviación estándar:\(s_e\) será un estimador para\(\sigma\)

Línea de regresión:\(\hat{Y}=b_{0}+b_{1} X\)

Ejemplo

Tomemos el ejemplo comparando la lluvia con las ventas de gafas de sol en las que la gráfica de dispersión muestra una correlación negativa. No obstante, hay muchas líneas que podríamos dibujar. ¿Cómo encontramos la línea de mejor ajuste?

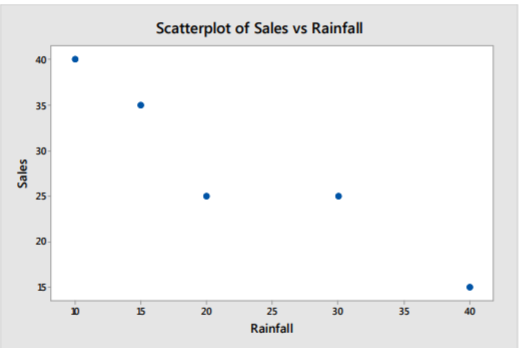
Solución

Minimización de la suma de errores residuales cuadrados (SSE)

Vamos a definir la “mejor línea” como la línea que minimiza la Suma de Errores Residuales Cuadrados (SSE).

Supongamos que tratamos de ajustar estos datos con una línea que pasa por el primer y último punto. Luego podemos calcular la ecuación de esta línea usando álgebra:

\[\hat{Y}=\dfrac{145}{3}-\dfrac{5}{6} X \approx 48.3-0.833 X \nonumber \]

El SSE para esta línea es 47.917:

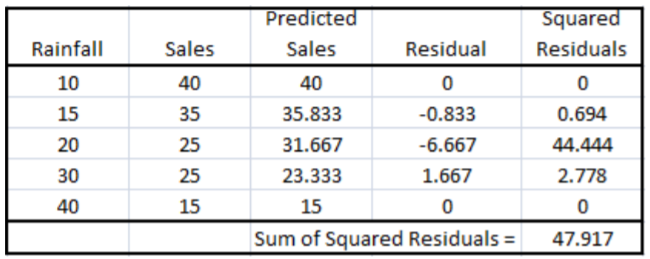
A pesar de que esta línea es un buen ajuste, no es la mejor línea. La pendiente (\(b_1\)) y la intercepción (\(b_o\)) para la línea que minimiza SSE se calculan usando las fórmulas principales de mínimos cuadrados:

Fórmulas principales de mínimos cuadrados

\(S S X=\Sigma X^{2}-\dfrac{1}{n}(\Sigma X)^{2}\)

\(S S Y=\Sigma Y^{2}-\dfrac{1}{n}(\Sigma Y)^{2}\)

\(S S X Y=\Sigma X Y-\dfrac{1}{n}(\Sigma X \cdot \Sigma y)\)

\(b_{1}=\dfrac{S S X Y}{S S X}\)

\(b_{0}=\bar{Y}-b_{1} \bar{X}\)

En el ejemplo de Lluvia donde\(X\) =Lluvia y\(Y\) =Ventas de Gafas de Sol:

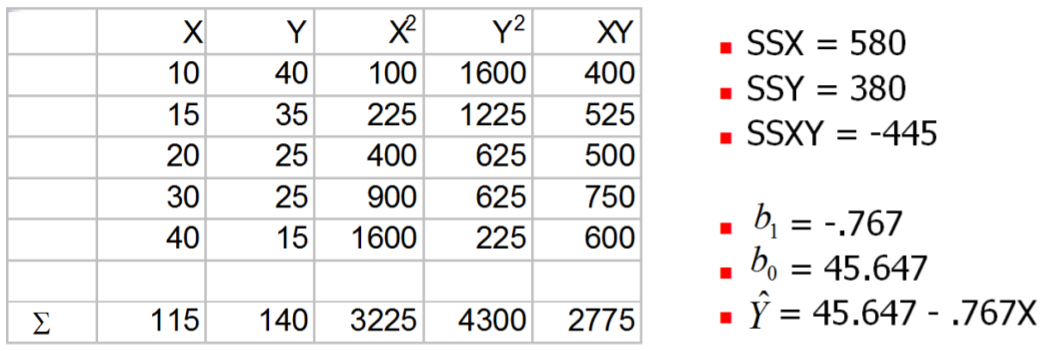
La Suma de Errores Residuales Cuadrados (SSE) para esta línea es de 38.578, lo que la convierte en la “mejor línea”. (Compare con el valor anterior, en el que escogimos la línea que se ajuste perfectamente a los dos puntos más extremos).

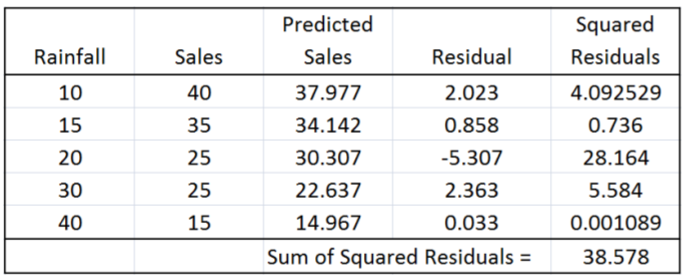
En la práctica, utilizaremos tecnología como Minitab para calcular esta línea. Aquí está el ejemplo usando la opción Gráfica de línea ajustada por regresión en Minitab, que determina y grafica la ecuación de regresión. El punto (20,25) tiene el mayor error residual, pero se minimiza la Suma de Errores Residuales Cuadrados (SSE).