5.2: La distribución normal estándar
- Page ID
- 151161
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
Objetivos de aprendizaje
- Aprender qué es una variable aleatoria normal estándar.
- Aprender a calcular probabilidades relacionadas con una variable aleatoria normal estándar.
Definición: variable aleatoria normal estándar
Una variable aleatoria normal estándar es una variable aleatoria normalmente distribuida con media\(\mu =0\) y desviación estándar\(\sigma =1\). Siempre se denotará con la letra\(Z\).
La función de densidad para una variable aleatoria normal estándar se muestra en la Figura\(\PageIndex{1}\).
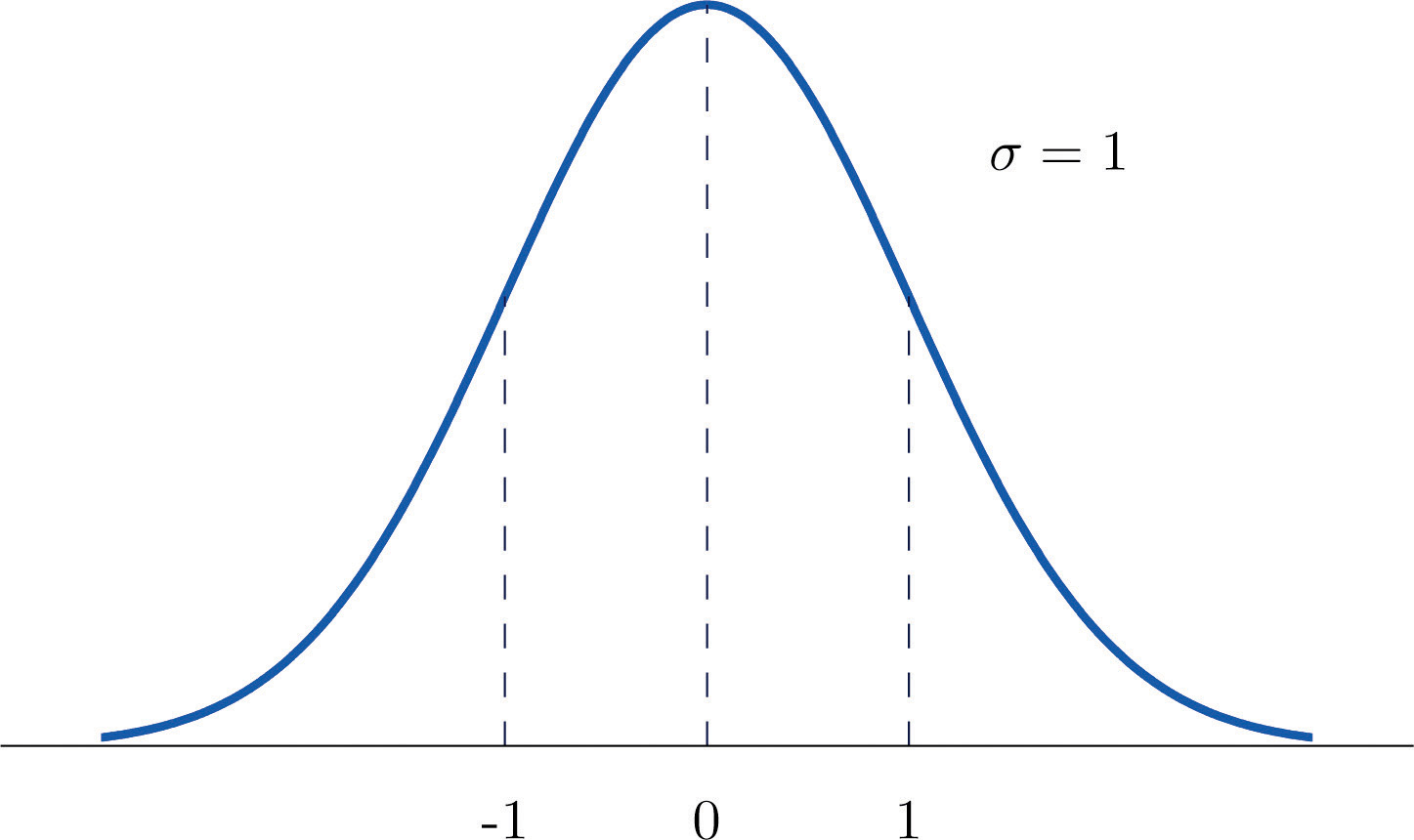
Para calcular las probabilidades no\(Z\) trabajaremos directamente con su función de densidad, sino que leeremos probabilidades de la Figura\(\PageIndex{2}\). Las tablas son tablas de probabilidades acumuladas; sus entradas son probabilidades de la forma\(P(Z< z)\). El uso de las tablas será explicado por la siguiente serie de ejemplos.
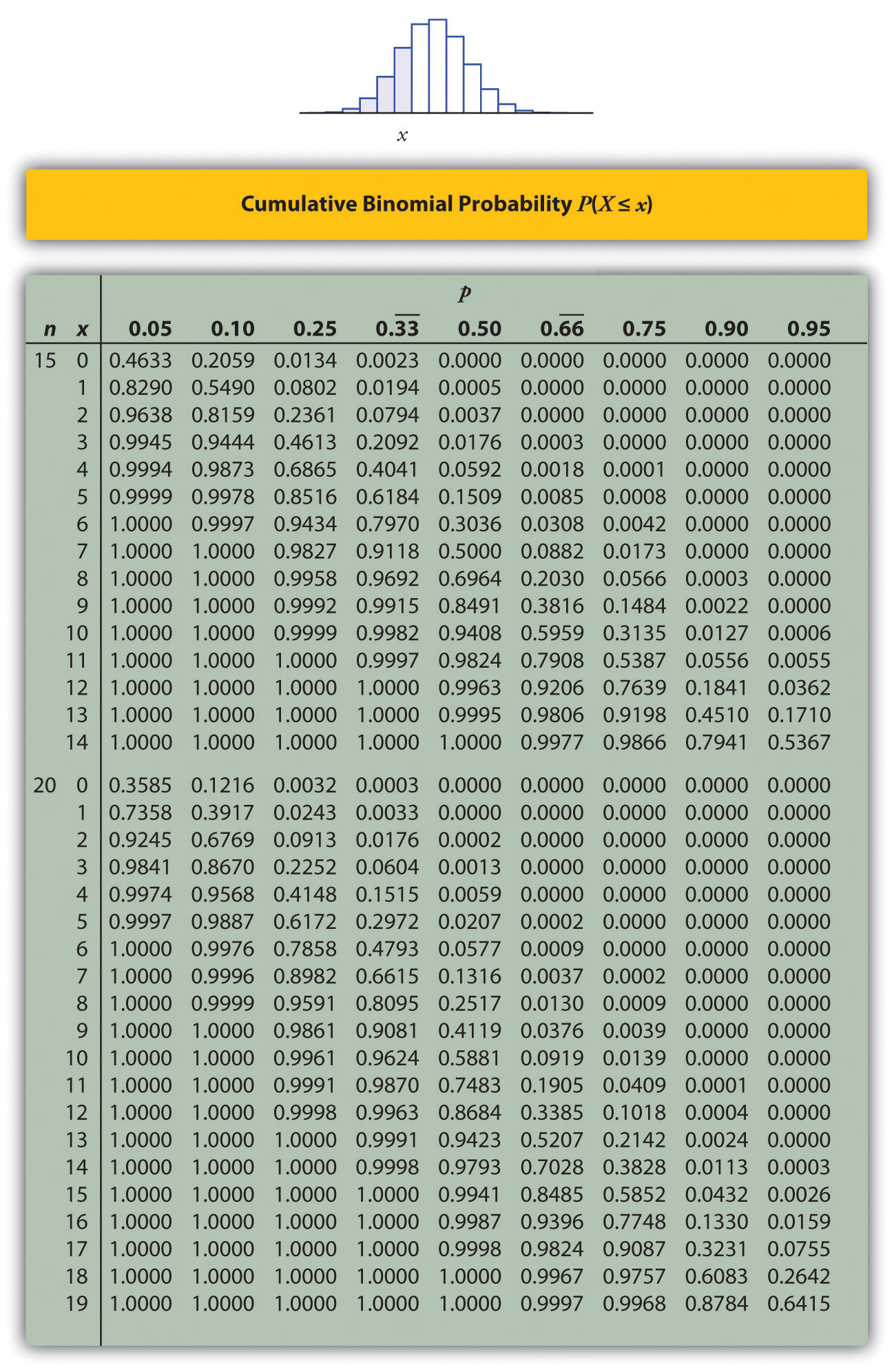
Ejemplo\(\PageIndex{1}\)
Encuentra las probabilidades indicadas, donde como siempre\(Z\) denota una variable aleatoria normal estándar.
- \(P(Z< 1.48)\).
- \(P(Z< -0.25)\).
Solución:
- La figura\(\PageIndex{3}\) muestra cómo se lee esta probabilidad directamente de la tabla sin que se requiera ningún cálculo. Los dígitos en los lugares unos y décimos de\(1.48\), es decir\(1.4\), se utilizan para seleccionar la fila apropiada de la tabla; la parte centésima de\(1.48\), es decir\(0.08\), se utiliza para seleccionar la columna apropiada de la tabla. El número de cuatro decimales en el interior de la tabla que se encuentra en la intersección de la fila y columna seleccionada,\(0.9306\), es la probabilidad buscada:
\[P(Z< 1.48)=0.9306\]
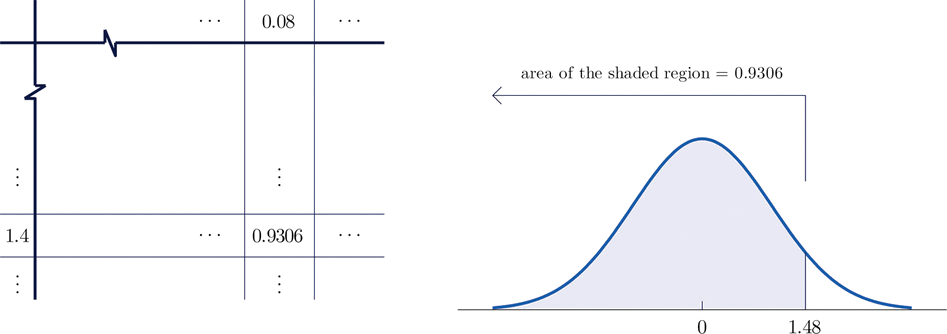
- El signo menos en el procedimiento no\(-0.25\) hace diferencia; la tabla se usa exactamente de la misma manera que en la parte (a): la probabilidad buscada es el número que se encuentra en la intersección de la fila con encabezado\(-0.2\) y la columna con encabezado\(0.05\), el número\(0.4013\). Así\(P(Z< -0.25)=0.4013\).
Ejemplo\(\PageIndex{2}\)
Encuentra las probabilidades indicadas.
- \(P(Z> 1.60)\).
- \(P(Z> -1.02)\).
Solución:
- Debido a que los eventos\(Z> 1.60\) y\(Z\leq 1.60\) son complementos, la Regla de Probabilidad para Complementos implica que\[P(Z> 1.60)=1-P(Z\leq 1.60)\] Dado que la inclusión del punto final no hace diferencia para la variable aleatoria continua\(Z\)\(P(Z\leq 1.60)=P(Z< 1.60)\),, que sabemos encontrar a partir de la tabla en la Figura \(\PageIndex{2}\). El número en la fila con encabezado\(1.6\) y en la columna con encabezado\(0.00\) es\(0.9452\).
P ( Z < 1.60 ) = 0.9452 " role="presentation" style="position:relative;" tabindex="0">\(P(Z< 1.60)=0.9452\)Así que\[P(Z> 1.60)=1-P(Z\leq 1.60)=1-0.9452=0.0548\] Figura\(\PageIndex{4}\) ilustra las ideas geométricamente. Dado que el área total bajo la curva es\(1\) y el área de la región a la izquierda de\(1.60\) es (de la tabla)\(0.9452\), el área de la región a la derecha de\(1.60\) debe ser1 − 0.9452 = 0.0548 . " role="presentation" style="position:relative;" tabindex="0">\(1-0.9452=0.0548\).
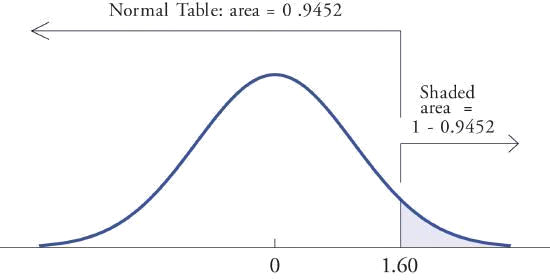
- El signo menos no\(-1.02\) hace diferencia en el procedimiento; la tabla se usa exactamente de la misma manera que en la parte (a). El número en la intersección de la fila con encabezado\(-1.0\) y la columna con encabezado\(0.02\) es\(0.1539\). Esto significa que\(P(Z<-1.02)=P(Z\leq -1.02)=0.1539\). De ahí\[P(Z>-1.02)=P(Z\leq -1.02)=1-0.1539=0.8461\]
Ejemplo\(\PageIndex{3}\)
Encuentra las probabilidades indicadas.
- \(P(0.5<Z<1.57)\).
- \(P(-2.55<Z<0.09)\).
Solución:
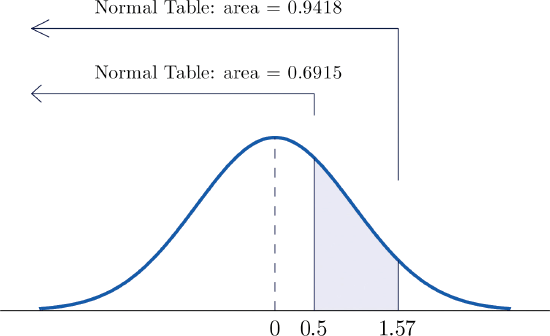
- La figura\(\PageIndex{5}\) ilustra las ideas involucradas para intervalos de este tipo. Primero busque las áreas en la tabla que corresponden a los números\(0.5\) (que pensamos como\(0.50\) para usar la tabla) y\(1.57\). Obtenemos\(0.6915\) y\(0.9418\), respectivamente. De la figura es evidente que debemos tomar la diferencia de estos dos números para obtener la probabilidad deseada. En símbolos,\[P(0.5<Z<1.57)=P(Z<1.57)-P(Z<0.50)=0.9418-0.6915=0.2503\]
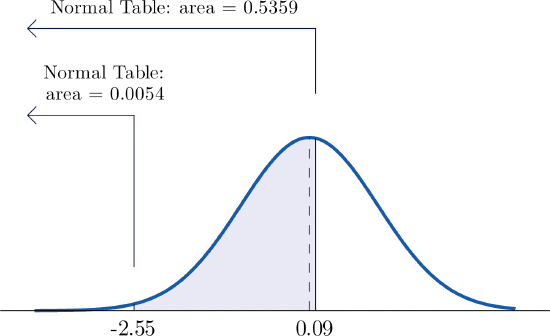
- El procedimiento para encontrar la probabilidad que\(Z\) toma un valor en un intervalo finito cuyos extremos tienen signos opuestos es exactamente el mismo procedimiento utilizado en la parte (a), y se ilustra en la Figura\(\PageIndex{6}\) “Computación de una Probabilidad para un Intervalo de Longitud Finita”. En símbolos el cálculo es\[P(-2.55<Z<0.09)=P(Z<0.09)-P(Z<-2.55)=0.5359-0.0054=0.5305\]
El siguiente ejemplo muestra qué hacer si el valor de lo\(Z\) que queremos buscar en la tabla no está presente ahí.
Ejemplo\(\PageIndex{4}\)
Encuentra las probabilidades indicadas.
- \(P(1.13<Z<4.16)\).
- \(P(-5.22<Z<2.15)\).
Solución:
- Intentamos calcular la probabilidad exactamente como en Ejemplo buscando\(\PageIndex{3}\) los números\(1.13\) y\(4.16\) en la tabla. Obtenemos el valor\(0.8708\) para el área de la región bajo la curva de densidad a la izquierda de\(1.13\) sin ningún problema, pero cuando vamos a buscar el número\(4.16\) en la tabla, no está ahí. Podemos ver desde la última fila de números en la tabla que el área a la izquierda de\(4.16\) debe estar tan cerca de 1 que a cuatro decimales se redondea a\(1.0000\). Por lo tanto\[P(1.13<Z<4.16)=1.0000-0.8708=0.1292\]
- De igual manera, aquí podemos leer directamente de la tabla que el área bajo la curva de densidad y a la izquierda de\(2.15\) está\(0.9842\), pero\(-5.22\) está demasiado lejos a la izquierda en la recta numérica para estar en la tabla. Podemos ver desde la primera línea de la tabla que el área a la izquierda de\(-5.22\) debe estar tan cerca de\(0\) esa a cuatro decimales a la que redondea\(0.0000\). Por lo tanto\[P(-5.22<Z<2.15)=0.9842-0.0000=0.9842\]
El último ejemplo de esta sección explica el origen de las proporciones dadas en la Regla Empírica.
Ejemplo\(\PageIndex{5}\)
Encuentra las probabilidades indicadas.
- \(P(-1<Z<1)\).
- \(P(-2<Z<2)\).
- \(P(-3<Z<3)\).
Solución:
- Usando la tabla como se hizo en Ejemplo\(\PageIndex{3}\) obtenemos\[P(-1<Z<1)=0.8413-0.1587=0.6826\] Since\(Z\) tiene media\(0\) y desviación estándar\(1\),\(Z\) para tomar un valor entre\(-1\) y\(1\) medias que\(Z\) toma un valor que está dentro de una desviación estándar de la media. Nuestro cálculo muestra que la probabilidad de que esto suceda es aproximadamente\(0.68\), la proporción dada por la Regla Empírica para histogramas que tienen forma de montículo y simétricos, como la curva de campana.
- Utilizando la tabla de la misma manera,\[P(-2<Z<2)=0.9772-0.0228=0.9544\] Esto corresponde a la proporción 0.95 para los datos dentro de dos desviaciones estándar de la media.
- De igual manera,\[P(-3<Z<3)=0.9987-0.0013=0.9974\] lo que corresponde a la proporción 0.997 para datos dentro de tres desviaciones estándar de la media.
Llave para llevar
- Una variable aleatoria normal estándar\(Z\) es una variable aleatoria normalmente distribuida con media\(\mu =0\) y desviación estándar\(\sigma =1\).
- Las probabilidades para una variable aleatoria normal estándar se calculan usando la Figura\(\PageIndex{2}\).