1.10: Espacios métricos

\(\newcommand{\R}{\mathbb{R}}\)\(\newcommand{\N}{\mathbb{N}}\)\(\newcommand{\diam}{\text{diam}}\)\(\newcommand{\bs}{\boldsymbol}\)\(\newcommand{\cl}{\text{cl}}\)

Teoría Básica

La mayoría de los espacios topológicos importantes que ocurren en las aplicaciones (como probabilidad) tienen una estructura adicional que da una distancia entre puntos en el espacio.

Definiciones

Un espacio métrico consiste en un conjunto no vacío\( S \) y una función\( d: S \times S \to [0, \infty) \) que satisface los siguientes axiomas: For\( x, \, y, \, z \in S \),

1. \( d(x, y) = 0 \)si y sólo si\( x = y \).
2. \( d(x, y) = d(y, x) \).
3. \( d(x, z) \le d(x, y) + d(y, z) \).

La función\( d \) se conoce como función métrica o de distancia.

Entonces como su nombre indica,\( d(x, y) \) es la distancia entre puntos\( x, \, y \in S \). Los axiomas están destinados a capturar las propiedades esenciales de la distancia desde la geometría. La parte (a) es la propiedad positiva; la distancia es estrictamente positiva si y sólo si los puntos son distintos. La parte (b) es la propiedad simétrica; la distancia de\( x \) a\( y \) es la misma que la distancia de\( y \) a\( x \). La parte (c) es la desigualdad triangular; pasar de\( x \) a\( z \) no puede ser más largo que ir de\( x \) a\( z \) por medio de un tercer punto\( y \).

Tenga en cuenta que si\( (S, d) \) es un espacio métrico, y\( A \) es un subconjunto no vacío de\( S \), entonces el conjunto\( A \) con\( d \) restringido a\( A \times A \) es también un espacio métrico (conocido como subespacio). Las siguientes definiciones también provienen naturalmente de la geometría:

Supongamos que\( (S, d) \) es un espacio métrico, y eso\( x \in S \) y\( r \in (0, \infty) \).

1. \( B(x, r) = \{y \in S: d(x, y) \lt r\} \)es la bola abierta con centro\( x \) y radio\( r \).
2. \( C(x, r) = \{y \in S: d(x, y) \le r\} \)es la bola cerrada con centro\( x \) y radio\( r \).

Una métrica en un espacio induce una topología en el espacio de manera natural.

Supongamos que\( (S, d) \) es un espacio métrico. Por definición, un conjunto\( U \subseteq S \) está abierto si por cada\( x \in U \) existe\( r \in (0, \infty) \) tal que\( B(x, r) \subseteq U \). La colección\( \mathscr S_d \) de subconjuntos abiertos de\( S \) es una topología.

Prueba

1. Trivialmente\( S \) está abierto y vacío\( \emptyset \) está abierto.
2. Supongamos que\( A_i \) está abierto para\( i \) en un conjunto de índices arbitrarios\( I \), y vamos\( A = \bigcup_{i \in I} A_i \). Si\( x \in A \) entonces\( x \in A_i \) para algunos\( i \in I \). Ya que\( A_i \) está abierto, existe\( r \in (0, \infty) \) con\( B(x, r) \subseteq A_i \). Pero entonces\( B(x, r) \subseteq A \) así\( A \) está abierto.
3. Supongamos que\( A_i \) está abierto para\( i \) en un conjunto de índices finitos\( I \), y let\( A = \bigcap_{i \in I} A_i \). Si\( x \in A \) entonces\( x \in A_i \) por cada\( i \in I \). De ahí que para cada uno\( i \in I \) exista\( r_i \in (0, \infty) \) tal que\( B(x, r_i) \subseteq A_i \). Vamos\( r = \min\{r_i: i \in I\} \). Ya que\( I \) es finito,\( r \gt 0 \) y\( B(x, r) \subseteq B(x, r_i) \subseteq A_i \) para cada uno\( i \in I \). De ahí\( B(x, r) \subseteq A \) que así\( A \) sea abierto.

Como sugieren los nombres, una bola abierta es de hecho abierta y una bola cerrada de hecho está cerrada.

Supongamos nuevamente que\( (S, d) \) es un espacio métrico, y eso\( x \in S \) y\( r \in (0, \infty) \). Entonces

1. \( B(x, r) \)está abierto.
2. \( C(x, r) \)está cerrado.

Prueba

1. Vamos\( y \in B(x, r) \), y vamos\( a = d(x, y) \), así que eso\( a \lt r \). Si\( z \in B(y, r - a) \) entonces tenemos\( d(x, y) = a \) y\( d(y, z) \lt r - a \), así por el triángulo de la desigualdad,\( d(x, z) \lt a + (r - a) = r \). De ahí\( z \in B(x, r) \). Así\( B(y, r - a) \subseteq B(x, r) \). De ello se deduce que\( B(x, r) \) está abierto
2. Demostramos que\( U = \left[C(x, r)\right]^c \) está abierto. Supongamos eso\( y \in U \), y vamos\( a = d(x, y) \), así que eso\( a \gt r \). Dejemos\( z \in B(y, a - r) \) y supongamos eso\( z \in C(x, r) \), así que eso\( d(z, x) \le r \). Por el triángulo de nuevo la desigualdad,\[ d(x, y) \le d(x, z) + d(z, y) \lt r + (a - r) = a \] una contradicción. De ahí\( z \in U \). Entonces\( B(y, a - r) \subseteq U \).

Recordemos que para un espacio topológico general, un barrio de un punto\( x \in S \) es un conjunto\( A \subseteq S \) con la propiedad\( U \) con la que existe un conjunto abierto\( x \in U \subseteq A \). De ello se deduce que en un espacio métrico,\( A \subseteq S \) es un barrio de\( x \) si y sólo si existe\( r \gt 0 \) tal que\( B(x, r) \subseteq A \). En palabras, un barrio de un punto debe contener una bola abierta sobre ese punto.

Es fácil construir nuevas métricas a partir de las que ya tenemos. Aquí hay uno de esos resultados.

Supongamos que\( S \) es un conjunto no vacío, y que\( d, \, e \) son métricas en\( S \), y\( c \in (0, \infty) \). Entonces las siguientes son también métricas sobre\( S \):

1. \( c d \)
2. \( d + e \)

Prueba

1. Recordemos que\( c d \) es la función definida por\( (c d)(x, y) = c d(x, y) \) for\( (x, y) \in S^2 \). Ya que\( c \gt 0 \), es fácil ver que los axiomas están satisfechos.
2. Recordemos que\( d + e \) es la función definida por\( (d + e)(x, y) = d(x, y) + e(x, y) \) for\( (x, y) \in S^2 \). Nuevamente, es fácil ver que los axiomas están satisfechos.

Dado que un espacio métrico produce un espacio topológico, todas las definiciones para espacios topológicos generales también se aplican a los espacios métricos. En particular, en un espacio métrico, siempre se pueden separar puntos distintos.

Un espacio métrico\( (S, d) \) es un espacio Hausdorff.

Prueba

\( x, \, y \)Dejen ser distintos puntos en\( S \). Entonces\(r = d(x, y) \gt 0\). Los conjuntos\( B(x, r/2) \) y\( B(y, r/2) \) están abiertos, y contienen\( x \) y\( y \), respectivamente. Supongamos que\( z \in B(x, r/2) \cap B(y, r/2) \). Por el triángulo la desigualdad,\[ d(x, y) \le d(x, z) + d(z, y) \lt \frac{r}{2} + \frac{r}{2} = r \] una contradicción. De ahí\( B(x, r/2) \) y\( B(y, r/2) \) son disjuntas.

Espacios Metrizables

Nuevamente, cada espacio métrico es un espacio topológico, pero no a la inversa. Un espacio no Hausdorff, por ejemplo, no puede corresponder a un espacio métrico. Sabemos que hay tales espacios; un conjunto\( S \) con más de un punto, y con la topología trivial\( \mathscr S = \{S, \emptyset\} \) es no-Hausdorff.

Supongamos que\( (S, \mathscr S) \) es un espacio topológico. Si existe una métrica\( d \) sobre\( S \) tal eso\( \mathscr S = \mathscr S_d \), entonces\( (S, \mathscr S) \) se dice que es metrizable.

Es fácil ver que diferentes métricas pueden inducir la misma topología. Por ejemplo, si\( d \) es una métrica y\( c \in (0, \infty) \), entonces las métricas\( d \) e\( c d \) inducen la misma topología.

Dejar\( S \) ser un conjunto no vacío. Métricas\( d \) y\( e \) on\(S\) son equivalentes, y escribimos\( d \equiv e \), si\( \mathscr S_d = \mathscr S_e \). La relación\( \equiv \) es una relación de equivalencia sobre la recopilación de métricas sobre\( S \). Es decir, para métricas\( d, \, e, \, f \) sobre\( S \),

1. \( d \equiv d \), la propiedad reflexiva.
2. Si\( d \equiv e \) entonces\( e \equiv d \), la propiedad simétrica.
3. Si\( d \equiv e \) y\( e \equiv f \) entonces\( d \equiv f \), la propiedad transitiva.

Existe una condición simple que caracteriza cuando la topología de una métrica es más fina que la topología de otra métrica, y entonces esto a su vez conduce a una condición de equivalencia de métricas.

Supongamos nuevamente que\( S \) es un conjunto no vacío y que\( d, \, e \) son métricas en\( S \). Entonces\( \mathscr S_e \) es más fino que\( \mathscr S_d \) si y sólo si cada bola abierta relativa a\( d \) contiene una bola abierta relativa a\( e \).

Prueba

Supongamos que\( \mathscr S_d \subseteq \mathscr S_e \) así\( \mathscr S_e \) es más fino que\( \mathscr S_d \). Si\( x \in S \) y\( a \in (0, \infty) \), entonces la bola abierta\( B_d(x, a) \) centrada en\( x \) el radio\( a \) para la métrica\( d \) está adentro\( \mathscr S_d \) y por lo tanto adentro\( \mathscr S_e \). Así existe\( b \in (0, \infty) \) tal que\( B_e(x, b) \subseteq B_d(x, a) \). Por el contrario, supongamos que la condición en el teorema sostiene y supongamos que\( U \in \mathscr S_d \). Si\( x \in U \) existe\( a \in (0, \infty) \) tal que\( B_d(x, a) \subseteq U \). De ahí que exista\( b \in (0, \infty) \) tal que\( B_e(x, b) \subseteq B_d(x, a) \subseteq U \). Entonces\( U \in \mathscr S_e \).

De ello se deduce que las métricas\( d \) y\( e \) on\( S \) son equivalentes si y solo si cada bola abierta relativa a una de las métricas contiene una bola abierta relativa a la otra métrica.

Entonces, cada topología metrizable en\( S \) corresponde a una clase de equivalencia de métricas que producen esa topología. A veces queremos saber que un espacio topológico es metrizable, por las buenas propiedades que tendrá, pero realmente no necesitamos usar una métrica específica que genere la topología. En todo caso, es importante tener condiciones suficientes para que un espacio topológico sea metrizable. El resultado más famoso es el teorema de la metrización de Urissohn, llamado así por el matemático ruso Pavel Urisshon:

Supongamos que\( (S, \mathscr S) \) es un espacio regular, segundo-contable, de Hausdorff. Entonces\( (S, \mathscr S) \) es metrizable.

Revisión de los términos

Recordemos que regular significa que cada conjunto cerrado y punto que no esté en el conjunto puede ser separado por conjuntos abiertos disjuntos. Como se discutió anteriormente, Hausdorff quiere decir que dos puntos distintos pueden ser separados por conjuntos abiertos disjuntos. Finalmente, segundo contable significa que hay una base contable para la topología, es decir, hay una colección contable de conjuntos abiertos con la propiedad de que cada otro conjunto abierto es una unión de conjuntos en la colección.

Convergencia

Con una función de distancia, la convergencia de una secuencia se puede caracterizar de una manera que es igual que el cálculo. Recordemos que para un espacio topológico general\( (S, \mathscr S) \), si\( (x_n: n \in \N_+) \) es una secuencia de puntos en\( S \) y\( x \in S \), entonces\( x_n \to x \) como\( n \to \infty \) medios que para cada barrio\( U \) de\( x \), existe\( m \in \N_+ \) tal que\( x_n \in U \) para\( n \gt m \).

Supongamos que\( (S, d) \) es un espacio métrico, y que\( (x_n: n \in \N_+) \) es una secuencia de puntos en\( S \) y\( x \in S \). Entonces\( x_n \to x \) como\( n \to \infty \) si y sólo si por cada\( \epsilon \gt 0 \) existe\( m \in \N_+ \) tal que si\( n \gt m \) entonces\( d(x_n, x) \lt \epsilon \). Equivalentemente,\( x_n \to x \) como\( n \to \infty \) si y sólo si\( d(x_n, x) \to 0 \) como\( n \to \infty \) (en el sentido habitual del cálculo).

Prueba

Supongamos que\( x_n \to x \) como\( n \to \infty \), y vamos\( \epsilon \gt 0 \). Entonces\( B(x, \epsilon) \) es un barrio de\( x \), entonces existe\( m \in \N_+ \) tal que\( x_n \in B(x, \epsilon) \) para\( n \gt m \), que es la condición en el teorema. Por el contrario, supongamos que esa condición en el teorema sostiene, y deja\( U \) ser un barrio de\( x \). Entonces existe\( \epsilon \gt 0 \) tal que\( B(x, \epsilon) \subseteq U \). Por suposición, existe\( m \in \N_+ \) tal que si\( n \gt m \) entonces\( x_n \in B(x, \epsilon) \subseteq U \).

Entonces, no importa cuán pequeños\( \epsilon \gt 0 \) puedan ser, todos menos finitamente muchos términos de la secuencia están\( \epsilon \) a distancia de\( x \). Como cabría esperar, los límites son únicos.

Supongamos nuevamente que\( (S, d) \) es un espacio métrico. Supongamos también que\( (x_n: n \in \N_+) \) es una secuencia de puntos en\( S \) y eso\( x, \, y \in S \). Si\( x_n \to x \) como\( n \to \infty \) y\( x_n \to y \) como\( n \to \infty \) entonces\( x = y \).

Prueba

Esto sigue inmediatamente ya que un espacio métrico es un espacio Hausdorff, y el límite de una secuencia en un espacio Hausdorff es único. Aquí hay una prueba directa: Vamos\( \epsilon \gt 0 \). Entonces existe\( k \in \N_+ \) tal que\( d(x_n, x) \lt \epsilon / 2 \) para\( n \gt k \), y existe\( m \in \N_+ \) tal que\( d(x_n, y) \lt \epsilon / 2 \) para\( n \gt m \). Vamos\( n \gt \max\{k, m\} \). Por el triángulo de la desigualdad,\[ d(x, y) \le d(x, x_n) + d(x_n, y) \lt \frac{\epsilon}{2} + \frac{\epsilon}{2} = \epsilon \] Así que tenemos\( d(x, y) \lt \epsilon \) para todos\( \epsilon \gt 0 \) y por lo tanto\( d(x, y) = 0 \) y así\( x = y \).

La convergencia de una secuencia es una propiedad topológica, por lo que se conserva bajo equivalencia de métricas.

Supongamos que\( d, \, e \) son métricas equivalentes en\( S \), y que\( (x_n: n \in \N_+) \) es una secuencia de puntos en\( S \) y\( x \in S \). Entonces\( x_n \to x \) como\( n \to \infty \) relativo a\( d \) si y solo si\( x_n \to x \) como\( n \to \infty \) relativo a\( e \).

Los subconjuntos cerrados de un espacio métrico tienen una caracterización simple en términos de secuencias convergentes, y esta caracterización es más intuitiva que los axiomas abstractos en un espacio topológico general.

Supongamos nuevamente que\( (S, d) \) es un espacio métrico. Entonces\( A \subseteq S \) se cierra si y sólo si siempre que una secuencia de puntos en\( A \) converge, el límite también está en\( A \).

Prueba

Supongamos que\( A \) está cerrado y que\( (x_n: n \in \N_+) \) es una secuencia de puntos en\( A \) con\( x_n \to x \in S \) as\( n \to \infty \). Supongamos que\( x \in A^c \). Ya que\( A^c \) está abierto,\( x_n \in A^c \) por\( n \) suficientemente grande, una contradicción. De ahí\( x \in A \). Por el contrario, supongamos que\( A \) tiene la propiedad de cierre secuencial, pero que no\( A \) está cerrada. Entonces no\( A^c \) está abierto. Esto quiere decir que existe\( x \in A^c \) con la propiedad en la que cada barrio\( x \) tiene puntos\( A \). Específicamente, para cada uno\( n \in \N_+ \) existe\( x_n \in B(x, 1/n) \) con\( x_n \in A \). Pero claramente\( x_n \to x \) como\( n \to \infty \), de nuevo una contradicción.

La siguiente definición también aparece en el cálculo estándar. La idea es tener un criterio de convergencia de una secuencia que no requiera conocer a priori el límite. Pero para los espacios métricos, esta definición cobra mayor importancia.

Supongamos nuevamente que\( (S, d) \) es un espacio métrico. Una secuencia de puntos\( (x_n: n \in \N_+) \) en\( S \) es una secuencia de Cauchy si por cada\( \epsilon \gt 0 \) existe\( k \in \N_+ \) tal que si\( m, \, n \in \N_+ \) con\( m \gt k \) y\( n \gt k \) luego\( d(x_m, x_n) \lt \epsilon \).

Las secuencias de Cauchy se llaman así por el ubicuo Augustin Cauchy. Entonces, para una secuencia de Cauchy, por muy pequeña que\( \epsilon \gt 0 \) sea, todos menos finitamente muchos términos de la secuencia estarán\( \epsilon \) a distancia unos de otros. Una secuencia convergente es siempre Cauchy.

Supongamos nuevamente que\( (S, d) \) es un espacio métrico. Si una secuencia de puntos\( (x_n: n \in \N_+) \) en\( S \) converge, entonces la secuencia es Cauchy.

Prueba

Por suposición, existe\( x \in S \) tal que\( x_n \to x \) como\( n \to \infty \). Vamos\( \epsilon \gt 0 \). Existe\( k \in \N_+ \) tal que si\( n \in \N_+ \) y\( n \gt k \) entonces\( d(x_n, x) \lt \epsilon / 2 \). De ahí si\( m, \, n \in \N_+ \) con\( m \gt k \) y\( n \gt k \) luego por la desigualdad del triángulo,\[ d(x_m, x_n) \le d(x_m, x) + d(x, x_n) \lt \frac{\epsilon}{2} + \frac{\epsilon}{2} = \epsilon \] Entonces la secuencia es Cauchy.

Por el contrario, uno podría pensar que una secuencia de Cauchy debería converger, pero es relativamente trivial crear una situación en la que esto sea falso. Supongamos que\( (S, d) \) es un espacio métrico, y que hay un punto\( x \in S \) que es el límite de una secuencia de puntos en\( S \) que todos son distintos de\( x \). Entonces el espacio\( T = S - \{x\} \) con la métrica\( d \) restringida a\( T \times T \) tiene una secuencia Cauchy que no converge. Esencialmente, hemos creado un agujero de convergencia. Por lo que nuestra siguiente definición es muy natural y muy importante.

Supongamos nuevamente que\( (S, d) \) es espacio métrico y eso\( A \subseteq S \). Entonces\( A \) se completa si cada secuencia de Cauchy en\( A \) converge a un punto en\( A \).

Por supuesto, la integridad se puede aplicar a todo el espacio\( S \). Trivialmente, un juego completo debe estar cerrado.

Supongamos nuevamente que\( (S, d) \) es un espacio métrico, y eso\( A \subseteq S \). Si\( A \) está completo, entonces\( A \) se cierra.

Prueba

Supongamos que\( \bs{x} = (x_n: n \in \N) \) es una secuencia de puntos en\( A \) y que\( x_n \to x \in S \) como\( n \to \infty \). Entonces\( \bs{x} \) es una secuencia de Cauchy, y así por completitud,\( x \in A \). De ahí\( A \) que esté cerrado por (12).

La integridad es una propiedad tan crucial que a menudo se impone como una suposición sobre los espacios métricos que ocurren en las aplicaciones. A pesar de que una secuencia de Cauchy puede no converger, aquí hay un resultado parcial que será útil último: si una secuencia de Cauchy tiene una subsecuencia convergente, entonces la secuencia misma converge.

Supongamos de nuevo el\( (S, d) \) es un espacio métrico, y eso\( (x_n: n \in \N_+) \) es una secuencia de Cauchy en\( S \). Si existe una subsecuencia\( \left(x_{n_k}: k \in \N_+\right) \) tal que\( x_{n_k} \to x \in S \) como\( k \to \infty \), entonces\( x_n \to x \) como\( n \to \infty \).

Prueba

Recordemos que en la construcción de una subsecuencia, los índices\( (n_k: k \in \N_+) \) deben ser una secuencia estrictamente creciente en\( \N_+ \). En particular,\( n_k \to \infty \) como\( k \to \infty \). Así que vamos\( \epsilon \gt 0 \). De las hipótesis, existe\( j \in \N_+ \) tal que si\( k \gt j \) entonces\( d\left(x_{n_k}, x\right) \lt \epsilon / 2 \). Existe\( N \in \N_+ \) tal que si\( m \gt N \) y\( p \gt N \) entonces\( d(x_m, x_p) \lt \epsilon / 2 \). Ahora vamos\( m \gt N \). Escoge\( k \in \N_+ \) tal que\( k \gt j \) y\( n_k \gt N \). Por la desigualdad triangular,\[ d(x_m, x) \le d\left(x_m, x_{n_k}\right) + d\left(x_{n_k}, x\right) \le \frac{\epsilon}{2} + \frac{\epsilon}{2} = \epsilon \]

Continuidad

En los espacios métricos, la continuidad de las funciones también tiene caracterizaciones simples en términos de que son familiares a partir del cálculo. Comenzamos con la continuidad local. Recordemos que la definición topológica general es que\( f: S \to T \) es continua en\( x \in S \) si\( f^{-1}(V) \) es un barrio de\( x \) adentro\( S \) para cada conjunto abierto\( V \) de\( f(x) \) in\( T \).

Supongamos que\( (S, d) \) y\( (T, e) \) son espacios métricos, y eso\( f: S \to T \). La continuidad de\( f \) at\( x \in S \) es equivalente a cada una de las siguientes condiciones:

1. Si\( (x_n: n \in \N_+) \) es una secuencia en\( S \) con\( x_n \to x \) como\( n \to \infty \) entonces\( f(x_n) \to f(x) \) como\( n \to \infty \).
2. Por cada\( \epsilon \gt 0 \), existe\( \delta \gt 0 \) tal que si\( y \in S \) y\( d(x, y) \lt \delta \) entonces\( e[f(y) - f(x)] \lt \epsilon \).

Prueba

1. Esta condición es continuidad secuencial en\( x \). La continuidad en\( x \) implica continuidad secuencial en\( x \) para espacios topológicos generales y, por lo tanto, para espacios métricos. Por el contrario, supongamos que la continuidad secuencial se mantiene en\( x \in S \), y deja\( V \) ser un barrio de\( f(x) \) adentro\( T \). Si no\( U = f^{-1}(V) \) es un barrio de\( x \) adentro\( S \), entonces para cada\( n \in \N_+ \), existe\(x_n \in B(x, 1/n) \) con\( x_n \notin U \). Pero entonces claramente\( x_n \to x \) como\( n \to \infty \) pero\( f(x_n) \) no converge a\( f(x) \) como\( n \to \infty \), una contradicción.
2. Supongamos que\( f \) es continuo en\( x \). Porque\( \epsilon \gt 0 \),\( B_T[f(x), \epsilon] \) es un barrio de\( f(x) \), y por lo tanto\( U = f^{-1}\left(B_T[f(x), \epsilon]\right) \) es un barrio de\( x \). De ahí que exista\( \delta \gt 0 \) tal que\( B_S(x, \delta) \subseteq U \). Pero esto quiere decir que si\( d(y, x) \lt \delta \) entonces\( e[f(y), f(x)] \lt \epsilon \). Por el contrario supongamos que la condición en (b) se mantiene, y supongamos que\( V \) es un barrio de\( f(x) \). Entonces existe\( \epsilon \gt 0 \) tal que\( B_T[f(x), \epsilon] \subseteq V \). Por asunción, existe\( \delta \gt 0 \) tal que si\( y \in B_S(x, \delta) \) entonces\( f(y) \in B_T[f(x), \epsilon] \subseteq V \). Esto quiere decir que\( f^{-1}(V) \) es un barrio de\( x \).

De manera más general, recordemos que\( f \) continuo en\( A \subseteq S \) significa que\( f \) es continuo en cada uno\( x \in A \), y ese\( f \) continuo significa que\( f \) es continuo en\(S \). Por lo que la continuidad general se puede caracterizar en términos de continuidad secuencial y la\( \delta \) condición\( \epsilon \) -.

En un espacio métrico, hay versiones más fuertes de continuidad.

Supongamos nuevamente eso\( (S, d) \) y\( (T, e) \) son espacios métricos y eso\( f: S \to T \). Entonces\( f \) es uniformemente continuo si por cada\( \epsilon \gt 0 \) existe\( \delta \gt 0 \) tal que si\( x, \, y \in S \) con\( d(x, y) \lt \delta \) entonces\( e[f(x), f(y)] \le \epsilon \).

En la\(\epsilon\) -\( \delta \) formulación de continuidad puntual ordinaria anterior,\( \delta \) depende del punto\( x \) además de\( \epsilon \). Con continuidad uniforme, existe un\( \delta \) dependiendo sólo de\( \epsilon \) que funciona de manera uniforme en\( x \in S \).

Supongamos de nuevo que\( (S, d) \) y\( (T, e) \) son espacios métricos, y eso\( f: S \to T \). Si\( f \) es uniformemente continuo entonces\( f \) es continuo.

Aquí hay una versión aún más fuerte de la continuidad.

Supongamos de nuevo que\( (S, d) \) y\( (T, e) \) son espacios métricos, y eso\( f: S \to T \). Entonces Höder\( f \) es continuo con exponente\( \alpha \in (0, \infty) \) si existe\( C \in (0, \infty) \) tal que\( e[f(x), f(y)] \le C [d(x, y)]^\alpha \) para todos\( x, \, y \in S \).

La definición lleva el nombre de Otto Höder. El exponente\( \alpha \) es más importante que la constante\( C \), que generalmente no tiene nombre. Si\( \alpha = 1 \),\( f \) se dice que es Lipschitz continuo, llamado así por el matemático alemán Rudolf Lipschitz.

Supongamos de nuevo que\( (S, d) \) y\( (T, e) \) son espacios métricos, y eso\( f: S \to T \). Si Höder\( f \) es continuo con exponente\( \alpha \gt 0 \) entonces\( f \) es uniformemente continuo.

El caso donde\( \alpha = 1 \) y\( C \lt 1 \) es particularmente importante.

Supongamos nuevamente eso\( (S, d) \) y\( (T, e) \) son espacios métricos. Una función\( f: S \to T \) es una contracción si existe\( C \in (0, 1) \) tal que\[ e[f(x), f(y)] \le C d(x, y), \quad x, \, y \in S \]

Así que las contracciones encogen la distancia. Por el resultado anterior, una contracción es uniformemente continua. Parte de la importancia de los mapas de contracción se debe al famoso teorema de punto fijo de Banach, llamado así por Stefan Banach.

Supongamos que\( (S, d) \) es un espacio métrico completo y eso\( f: S \to S \) es una contracción. Entonces\( f \) tiene un punto fijo único. Es decir, existe exactamente uno\( x^* \in S \) con\( f(x^*) = x^* \). Dejar\( x_0 \in S \), y definir recursivamente\( x_n = f(x_{n-1}) \) para\( n \in \N_+ \). Entonces\( x_n \to x^* \) como\( n \to \infty \).

Las funciones que preservan la distancia son particularmente importantes. El término isometría significa preservar la distancia.

Supongamos de nuevo que\( (S, d) \) y\( (T, e) \) son espacios métricos, y eso\( f: S \to T \). Entonces\( f \) es una isometría si\( e[f(x), f(y)] = d(x, y) \) por cada\( x, \, y \in S \).

Supongamos de nuevo que\( (S, d) \) y\( (T, e) \) son espacios métricos, y eso\( f: S \to T \). Si\( f \) es una isometría, entonces\( f \) es uno a uno y Lipschitz continuo.

Prueba

Si\( x, \, y \in S \) con\( x \ne y \), entonces\( e[f(x), f(y)] = d(x, y) \gt 0 \), así\( f(x) \ne f(y) \). De ahí\( f \) que sea uno a uno. Directamente desde la definición,\( f \) es Höder continuo con exponente\( \alpha = 1 \) y múltiple constante\( C = 1 \).

En particular, una isometría\( f \) es uniformemente continua. Si un espacio métrico se puede mapear isométricamente en otro espacio métrico, los espacios son esencialmente los mismos.

Espacios métricos\( (S, d) \) y\( (T, e) \) son isométricos si existe una isometría\( f \) que se mapee\( S \) sobre\( T \). La isometría es una relación de equivalencia en espacios métricos. Es decir, para espacios métricos\( (S, d) \)\( (T, e) \)\( (U, \rho) \), y

1. \( (S, d) \)es isométrico a\( (S, d) \), la propiedad reflexiva.
2. Si\( (S, d) \) es isométrico a\( (T, e) \) ellos\( (T, e) \) es isométrico a\( (S, d) \), la propiedad simétrica.
3. Si\( (S, d) \) es isométrico a\( (T, e) \) y\( (T, e) \) es isométrico a\( (U, \rho) \), entonces\( (S, d) \) es isométrico a\( (U, \rho) \), la propiedad transitiva.

Prueba

1. La función de identidad\( I: S \to S \) definida por\( I(x) = x \) for\( x \in S \) es una isometría de\( (S, d) \) hacia\( (S, d) \).
2. Si\( f \) es una isometría de\( (S, d) \) hacia\( (T, e) \), entonces\( f^{-1} \) es una isometría de\( (T, e) \) hacia\( (S, d) \).
3. Si\( f \) es una isometría de\( (S, d) \) hacia\( (T, e) \) y\( g \) es una isometría de\( (T, e) \) hacia\( (U, \rho) \), entonces\( g \circ f \) es una isometría de\( (S, d) \) a\( (U, \rho) \).

En particular, si los espacios métricos\( (S, d) \) y\( (T, e) \) son isométricos, entonces como espacios topológicos, son homeomórficos.

Compacidad y Boundedness

En un espacio métrico, diversas definiciones relacionadas con un conjunto delimitado son naturales, y están relacionadas con el concepto general de compacidad.

Supongamos nuevamente que\( (S, d) \) es un espacio métrico, y eso\( A \subseteq S \). Entonces\( A \) está acotado si existe\( r \in (0, \infty) \) tal que\( d(x, y) \le r \) para todos\( x, \, y \in A \). El diámetro de\( A \) es\[ \diam(A) = \inf\{r \gt 0: d(x, y) \lt r \text{ for all } x, \, y \in A\} \]

Detalles adicionales

Recordemos eso\( \inf(\emptyset) = \infty \), así que\(\diam(A) = \infty \) si\( A \) es sin límites. En el caso acotado, tenga en cuenta que si la distancia entre puntos en\( A \) está delimitada por\( r \in (0, \infty) \), entonces la distancia está delimitada por cualquiera\( s \in [r, \infty) \). De ahí que la definición del diámetro tenga sentido.

Así\( A \) está acotado si y sólo si\( \diam(A) \lt \infty \). El diámetro es una función creciente en relación con el orden parcial del subconjunto.

Supongamos nuevamente que\( (S, d) \) es un espacio métrico, y eso\( A \subseteq B \subseteq S \). Entonces\( \diam(A) \le \diam(B) \).

Nuestra siguiente definición es más fuerte, pero primero revisemos alguna terminología que usamos para los espacios topológicos generales: Si\( S \) es un conjunto,\( A \) un subconjunto de\( S \), y\( \mathscr{A} \) una colección de subconjuntos de\( S \), entonces\( \mathscr{A} \) se dice que cubre\( A \) si\( A \subseteq \bigcup \mathscr{A} \). Entonces con esta terminología, podemos hablar de cubiertas abiertas, cubiertas cerradas, cubiertas finitas, cubiertas disjuntas, etc.

Supongamos nuevamente que\( (S, d) \) es un espacio métrico, y eso\( A \subseteq S \). Entonces\( A \) está totalmente delimitado si por cada\( r \gt 0 \) hay una cubierta finita de\( A \) con bolas abiertas de radio\( r \).

Recordemos que para un espacio topológico general, un conjunto\( A \) es compacto si cada cubierta abierta de\( A \) tiene una subcubierta finita. Entonces en un espacio métrico, a veces se usa el término precompacto en lugar de totalmente acotado: El conjunto\( A \) está totalmente delimitado si cada cubierta de\( A \) con bolas abiertas de radio\( r \) tiene una subcubierta finita.

Supongamos nuevamente que\( (S, d) \) es un espacio métrico. Si\( A \subseteq S \) está totalmente acotado entonces\( A \) está acotado.

Prueba

Existe una cubierta finita de\( A \) con bolas abiertas de radio 1. Dejar\( C \) denotar el conjunto de centros de las bolas, y dejar\( c = \max\{d(u, v): u, \, v \in C\} \), la distancia máxima entre dos centros. Ya que\( C \) es finito,\( c \lt \infty \). Ahora vamos\( x, \, y \in A \). Ya que las bolas cubren\( A \), existen\( u, \, v \in C \) con\( x \in B(u, 1) \) y\( y \in B(v, 1) \). Por el triángulo desigualdad (¿qué más?) \[ d(x, y) \le d(x, u) + d(u, v) + d(v, y) \le 2 + c \]De ahí\( A \) está acotado.

Dado que un espacio métrico es un espacio Hausdorff, se cierra un subconjunto compacto de un espacio métrico. La compacidad también tiene una caracterización simple en términos de convergencia de secuencias.

Supongamos nuevamente que\( (S, d) \) es un espacio métrico. Un subconjunto\( C \subseteq S \) es compacto si y solo si cada secuencia de puntos en\( C \) tiene una subsecuencia que converge a un punto en\( C \).

Prueba

La condición en el teorema se conoce como compacidad secuencial, por lo que queremos mostrar que la compacidad secuencial es equivalente a la compacidad. La prueba es más dura que la mayoría de las otras en esta sección, pero la prueba que aquí se presenta es la más bonita que he encontrado, y se debe a Anton Schep.

Supongamos que\( C \) es compacto y que\( \bs{x} = (x_n: n \in \N_+) \) es una secuencia de puntos en\( C \). Let\( A = \{x_n: n \in \N_+\} \subseteq C\), el conjunto desordenado de puntos distintos en la secuencia. Si\( A \) es finito, entonces algún elemento de\( a \in A \) debe ocurrir infinitamente muchas veces en la secuencia. En este caso, podemos construir una subsecuencia de\( \bs{x} \) todos cuyos términos son\( a \), y así esta subsecuencia converge trivialmente a\( a \in C \). Supongamos que a continuación eso\( A \) es infinito. Dado que el espacio es Hausdorff,\( C \) está cerrado, y por lo tanto\( \cl(A) \subseteq C \). Nuestra siguiente afirmación es que existe\( a \in \cl(A) \) tal que para cada\( r \gt 0 \), el conjunto\( A \cap B(a, r) \) es infinito. Si el reclamo es falso, entonces para cada uno\( a \in \cl(A) \) existe\( r_a \gt 0 \) tal que\( A \cap B(a, r) \) es finito. Se deduce entonces que para cada uno\( a \in A \), existe\( \epsilon_a \gt 0 \) tal que\( A \cap B(a, \epsilon_a) = \{a\} \). Pero entonces\( \mathscr{U} = \{B(a, \epsilon_a): a \in \cl(A)\} \cup \{[\cl(A)]^c\} \) es una portada abierta de\( C \) que no tiene subcubierta finita, una contradicción. Entonces el reclamo es cierto y para algunos\( a \in \cl(A) \), el conjunto\( A \cap B(a, r) \) es infinito para cada uno\( r \gt 0 \). Podemos construir una subsecuencia de la\( \bs{x} \) que converja a\( a \in C \).

Por el contrario, supongamos que\( C \) es secuencialmente compacto. Si\( \bs{x} = (x_n: n \in \N_+) \) es una secuencia de Cauchy en\( C \), entonces por suposición,\( \bs{x} \) tiene una subsecuencia que converge a algunos\( x \in C \). Pero entonces por (17) la secuencia\( \bs{x} \) misma converge a\( x \), por lo que sigue que\( C \) está completa. A continuación mostramos que\( C \) está totalmente acotado. Nuestro objetivo es mostrar que\( C \) puede ser cubierto por un número finito de bolas de un radio arbitrario\( r \gt 0 \). Pick\( x_1 \in C \). Si\( C \subseteq B(x_1, r) \) entonces ya terminamos. De lo contrario, elige\( x_2 \in C \setminus B(x_1, r) \). Si\( C \subseteq B(x_1, r) \cup B(x_2, r) \) entonces otra vez hemos terminado. De lo contrario existe\( x_3 \in C \setminus [B(x_1, r) \cup B(x_2, r)] \). Este proceso debe terminar en un número finito de pasos o de lo contrario tendríamos una secuencia de puntos\( (x_n: n \in \N_+) \) en\( C \) con la propiedad que\( d(x_n, x_m) \ge r \) para cada\( n, \, m \in \N_+ \). Tal secuencia no tiene una subsecuencia convergente. Supongamos ahora que\( \mathscr{U} \) es una cubierta abierta de\( C \) y vamos\( c = \diam(C) \). Entonces\( C \) puede ser cubierto por un número finito de bolas cerradas de con centros dentro\( C \) y con radio\( c / 4 \). De ello se deduce que al menos una de estas bolas no puede ser cubierta por una subcubierta finita de\( \mathscr{U} \). Vamos a\( C_1 \) denotar la intersección de esta bola con\( C \). Luego\( C_1 \) se cierra y se compacta secuencialmente con\( \diam(C_1) \le c / 4 \). Repitiendo el argumento, generamos una secuencia anidada de conjuntos cercanos\( (C_1, C_2, \ldots) \) tales que\( \diam(C_n) \le c / 2^n \), y con la propiedad que\( C_n \) no puede ser cubierta finitamente por\( \mathscr{U} \) para cada uno\( n \in \N_+ \). Pick\( x_n \in C_n \) para cada uno\( n \in \N_+ \). Entonces\( \bs{x} = (x_n: n \in \N_+) \) es una secuencia de Cauchy en\( C \) y por lo tanto tiene una subsecuencia que converge a algunos\( x \in C \). Entonces\( x \in \bigcap_{n=1}^\infty C_n \) y\( \diam(C_n) \to 0 \) como se\( n \to \infty \) deduce que de hecho,\( \bigcap_{n=1}^\infty C_n = \{x\}\). Ahora, desde\( \mathscr{U} \) las coberturas\( C \), existe\( U \in \mathscr{U} \) tal que\( x \in U \). Ya que\( U \) está abierto, existe\( r \gt 0 \) tal que\( B(x, r) \subseteq U \). Ahora vamos a\( n \in \N_+ \) ser suficientemente grandes que\( d(x, x_n) \le r / 2 \) y\( \diam(C_n) \lt r / 2 \). Entonces\( C_n \subseteq B(x, r) \subseteq U \), lo que contradice el hecho de que\( C_n \) no puede cubrirse finitamente\( \mathscr{U} \).

Medida y dimensión de Hausdorff

Nuestra última discusión es algo avanzada, pero es importante para el estudio de ciertos procesos aleatorios, particularmente el movimiento browniano. La idea es medir el tamaño de un conjunto en un espacio métrico de manera topológica, y luego usar esta medida para definir un tipo de dimensión. Necesitamos una definición preliminar, utilizando nuestra conveniente terminología de cobertura. Si\( (S, d) \) es un espacio métrico,\( A \subseteq S \), y\( \delta \in (0, \infty) \), entonces una \( \delta \)cubierta contable de\( A \) es una cubierta contable\( \mathscr{B} \) de\( A \) con la propiedad que\( \diam(B) \lt \delta \) para cada uno\( B \in \mathscr{B} \).

Supongamos nuevamente que\( (S, d) \) es un espacio métrico y eso\( A \subseteq S \). Para\( \delta \in (0, \infty) \) y\( k \in [0, \infty) \), definir\[ H_\delta^k(A) = \inf\left\{\sum_{B \in \mathscr{B}} \left[\diam(B)\right]^k: \mathscr{B} \text{ is a countable } \delta \text{ cover of } A \right\} \] La medida\( k \) -dimensional de Hausdorff\( A \) es\[ H^k(A) = \sup \left\{H_\delta^k(A): \delta \gt 0\right\} = \lim_{\delta \downarrow 0} H_\delta^k(A) \]

Detalles adicionales

Tenga en cuenta que si\( \mathscr{B} \) es una\( \delta \) cubierta contable de\( A \) entonces también es una\( \epsilon \) cubierta contable de\( A \) para cada\( \epsilon \gt \delta \). Esto significa que\( H_\delta^k(A) \) está disminuyendo en\( \delta \in (0, \infty) \) para fijo\( k \in [0, \infty) \). De ahí\[ \sup \left\{H_\delta^k(A): \delta \gt 0\right\} = \lim_{\delta \downarrow 0} H_\delta^k(A) \]

Tenga en cuenta que la medida\( k \) -dimensional de Hausdorff se define para todos\( k \in [0, \infty) \), no solo enteros no negativos. Sin embargo, las dimensiones enteras son interesantes. La medida 0-dimensional de\( A \) es el número de puntos en\( A \). En el espacio euclidiano, que consideramos en (36), las medidas de las dimensiones 1, 2 y 3 están relacionadas con la longitud, el área y el volumen, respectivamente.

Supongamos nuevamente que\( (S, d) \) es un espacio métrico y eso\( A \subseteq S \). La dimensión de Hausdorff\( A \) es\[ \dim_H(A) = \inf\{k \in [0, \infty): H^k(A) = 0\} \]

De especial interés, como antes, es el caso cuando\( S = \R^n \) para algunos\( n \in \N_+ \) y\( d \) es la distancia euclidiana estándar, revisada en (36). Como se puede adivinar, la dimensión Hausdorff de un punto es 0, la dimensión Hausdorff de una curva simple es 1, la dimensión Hausdorff de una superficie simple es 2, y así sucesivamente. Pero también hay conjuntos con dimensión fraccional de Hausdorff, y el proceso estocástico El movimiento browniano proporciona algunos ejemplos fascinantes. La gráfica de movimiento browniano estándar tiene dimensión Hausdorff\( 3/2 \) mientras que el conjunto de ceros tiene dimensión Hausdorff\( 1/2 \).

Ejemplos y Casos Especiales

Espacios vectoriales normados

Una norma en un espacio vectorial genera una métrica sobre el espacio de una manera muy simple y natural.

Supongamos que\( (S, +, \cdot) \) es un espacio vectorial, y eso\( \| \cdot \| \) es una norma sobre el espacio. Entonces\( d \) definido por\( d(x, y) = \|y - x\| \) for\( x, \, y \in S \) es una métrica en\( S \).

Prueba

Los axiomas métricos se desprenden fácilmente de los axiomas normales.

1. La propiedad positiva para\( d \) sigue desde\( \|x\| = 0 \) si y solo si\( x = 0 \).
2. La propiedad simétrica para\( d \) sigue desde\( \|-x\| = \|x\| \).
3. La desigualdad triangular para\( d \) se desprende del triángulo desigualdad para la norma:\( \|x + y\| \le \|x\| + \|y\| \).

En\( \R^n \), tenemos una variedad de normas, y por lo tanto una variedad de métricas.

Para\( n \in \N_+ \) y\( k \in [1, \infty) \), la función\( d_k \) dada a continuación es una métrica en\( \R^n \):\[ d_k(\bs{x}, \bs{y}) = \left(\sum_{i=1}^n \left|x_i - y_i\right|^k\right)^{1/k}, \quad \bs{x} = (x_1, x_2, \ldots, x_n), \, \bs{y} = (y_1, y_2, \ldots, y_n) \in \R^n \]

Prueba

Esto se desprende del resultado general anterior, ya que a continuación se\( \| \cdot \|_k \) define una norma sobre\( \R^n \):\[ \| \bs{x} \|_k = \left(\sum_{i=1}^k \left|x_i\right|^k \right)^{1/k}, \quad \bs{x} = (x_1, x_2, \ldots, x_n) \in \R^n \]

Por supuesto que la métrica\( d_2 \) es la distancia euclidiana, llamada así por Euclides por supuesto. Este es el más importante, en sentido práctico porque es el habitual que usamos en el mundo real, y en un sentido matemático porque la norma asociada corresponde al producto interno estándar\( \R^n \) dado por\[ \langle \bs{x}, \bs{y} \rangle = \sum_{i=1}^n x_i y_i, \quad \bs{x} = (x_1, x_2, \ldots, x_n), \, \bs{y} = (y_1, y_2, \ldots, y_n) \in \R^n \]

Para\( n \in \N_+ \), la función\( d_\infty \) definida a continuación es una métrica en\( \R^n \):\[ d_\infty(\bs{x}, \bs{y}) = \max\{\left|x_i - y_i\right|: i \in \{1, 2 \ldots, n\}\}, \quad \bs{x} = (x_1, x_2, \ldots, x_n) \in \R^n \]

Prueba

Esto se desprende del resultado general anterior, ya que a continuación se\( \| \cdot \|_\infty \) define una norma sobre\( \R^n \):\[ \| \bs{x} \|_\infty = \max\{\left|x_i\right|: i \in \{1, 2, \ldots, n\}\}, \quad \bs{x} = (x_1, x_2, \ldots, x_n) \in \R^n \]

Para justificar la notación, recordemos que en\( \| \bs{x} \|_k \to \|\bs{x}\|_\infty \) cuanto\( k \to \infty \) a\( \bs{x} \in \R^n \), y por lo tanto en\( d_k(\bs{x}, \bs{y}) \to d_\infty(\bs{x}, \bs{y}) \)\( k \to \infty \) cuanto a\( \bs{x}, \bs{y} \in \R^n\).

Figura\(\PageIndex{1}\): De adentro hacia afuera, los límites de las bolas unitarias centradas en el origen en\( \R^2 \) para las métricas\( d_k \) con\( k \in \{1, 3/4, 2, 3, \infty\} \).

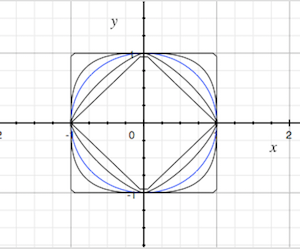
Supongamos ahora que\( S \) es un conjunto no vacío. Recordemos que la colección\( \mathscr{V} \) de todas las funciones\( f: S \to \R \) es un espacio vectorial bajo la definición puntual habitual de suma y multiplicación escalar. Es decir, si\( f, \, g \in \mathscr{V} \) y\( c \in \R \), entonces\( f + g \in \mathscr{V} \) y\( c f \in \mathscr{V} \) se definen por\( (f + g)(x) = f(x) + g(x) \) y\( (c f)(x) = c f(x) \) para\( x \in S \). Recordemos además que la colección\( \mathscr{U} \) de funciones acotadas\(f: S \to \R \) es un subespacio vectorial de\( \mathscr{V} \), y además,\( \| \cdot \| \) definido por\( \| f \| = \sup\{\left| f(x) \right|: x \in S\} \) es una norma sobre\( \mathscr{U} \), conocida como la norma suprema. Se deduce que\( \mathscr{U} \) es un espacio métrico con la métrica\( d \) definida por los espacios\[ d(f, g) = \| f - g \| = \sup\{\left|f(x) - g(x)\right|: x \in S\} \] vectoriales de funciones delimitadas, de valor real, con la norma suprema son muy importantes en el estudio de la probabilidad y los procesos estocásticos. Obsérvese que la norma suprema sobre\( \mathscr{U} \) generaliza la norma máxima en\( \R^n \), ya que podemos pensar en un punto en\( \R^n \) como una función de\( \{1, 2, \ldots, n\} \) hacia dentro\( \R \). Posteriormente, como parte de nuestra discusión sobre la integración con respecto a una medida positiva, veremos cómo generalizar las\( k \) normas sobre\( \R^n \) a espacios de funciones.

Productos de Espacios Métricos

Si tenemos un número finito de espacios métricos, entonces podemos combinar las métricas individuales, junto con una norma sobre el espacio vectorial\( \R^n \), para crear una norma sobre el espacio de productos cartesianos.

Supongamos\( n \in \{2, 3, \ldots\} \), y ese\( (S_i, d_i) \) es un espacio métrico para cada uno\( in \in \{1, 2, \ldots, n\} \). Supongamos también que\( \| \cdot \| \) es una norma sobre\( \R^n \). Entonces la función\( d \) dada de la siguiente manera es una métrica en\( S = S_1 \times S_2 \times \cdots \times S_n \):\[ d(\bs{x}, \bs{y}) = \left\|\left(d_1(x_1, y_1), d_2(x_2, y_2), \ldots, d_n(x_n, y_n)\right)\right\|, \quad \bs{x} = (x_1, x_2, \ldots, x_n), \, \bs{y} = (y_1, y_2, \ldots, y_n) \in S \]

Prueba

1. Tenga en cuenta que\( d(\bs{x}, \bs{y}) = 0 \) si y solo\( i \in \{1, 2, \ldots, n\} \) si\( d_i(x_i, y_i) = 0 \) para si y solo si\( x_i = y_i \) para\( i \in \{1, 2, \ldots, n\} \) si y solo si\( \bs{x} = \bs{y} \).
2. Ya que\( d_i(x_i, y_i) = d_i(y_i, x_i) \) para\( i \in \{1, 2, \ldots, n\} \), tenemos\( d(\bs{x}, \bs{y}) = d(\bs{y}, \bs{x}) \).
3. La desigualdad triangular se deriva de la desigualdad del triángulo para cada métrica, y la desigualdad del triángulo para la norma.

Gráficas

Recordemos que una gráfica (en el sentido combinatorio) consiste en un conjunto contable\( S \) de vértices y un conjunto\( E \subseteq S \times S \) de aristas. En esta discusión, asumimos que la gráfica está desdirigida en el sentido de que\( (x, y) \in E \) si y solo si\( (y, x) \in E \), y no tiene bucles\( (x, x) \notin E \) para que para\( x \in S \). Por último, recordemos que un camino\( n \in \N_+ \) de longitud de\( x \in S \) a\( y \in S \) es una secuencia\( (x_0, x_1, \ldots, x_n) \in S^{n+1} \) tal que\( x_0 = x \),\( x_n = y \), y\( (x_{i-1}, x_i) \in E \) para\( i \in \{1, 2, \ldots, n\} \). La gráfica está conectada si existe una ruta de longitud finita entre dos vértices distintos cualesquiera en\( S \). Tal gráfica tiene una métrica natural:

Supongamos que\( G = (S, E) \) es una gráfica conectada. Luego\( d \) se define de la siguiente manera una métrica en\( S \):\( d(x, x) = 0 \) para\( x \in S \), y\( d(x, y) \) es la longitud del camino más corto de\( x \) a\( y \) para distinto\( x, \, y \in S \).

Prueba

1. La propiedad positiva se desprende de la definición:\( d(x, y) = 0 \) si y solo si\( x = y \)
2. La propiedad simétrica sigue ya que la gráfica no está dirigida:\( d(x, y) = d(y, x) \) para todos\( x, \, y \in S \).
3. Para la desigualdad triangular, supongamos que\( x, \, y, \, z \in S \), y eso\( m = d(x, y) \) y\( n = d(y, z) \). Luego hay un camino de longitud\( m \) de\( x \) a\( y \) y un camino de longitud\( n \) de\( y \) a\( z \). Concatenar las rutas produce una ruta de longitud\( m + n \) de\( x \) a\( z \). Pero\( d(x, z) \) es la longitud del camino más corto de este tipo, por lo que se deduce de eso\( d(x, z) \le m + n \).

La Topología Discreta

Supongamos que\( S \) es un conjunto no vacío. Recordemos que la topología discreta\( S \) encendida es\( \mathscr{P}(S) \), el conjunto de potencia de\( S \), de modo que cada subconjunto de\( S \) está abierto (y cerrado). La topología discreta es metrizable, y hay muchas métricas que generan esta topología.

Supongamos nuevamente que\( S \) es un conjunto no vacío. Una métrica\( S \) con\( d \) la propiedad que existe\( c \in (0, \infty) \) tal que\( d(x, y) \ge c \) para distinto\( x, \, y \in S \) genera la topología discreta.

Prueba

Tenga en cuenta que\( B(x, c) = \{x\} \) para\( x \in S \). De ahí\( \{x\} \) que esté abierto para cada uno\( x \in S \).

Entonces, cualquier métrica que esté delimitada desde abajo (para puntos distintos) genera la topología discreta. Es fácil ver que existen tales métricas.

Supongamos nuevamente que\( S \) es un conjunto no vacío. La función\( d \) en\( S \times S \) definida por\( d(x, x) = 0 \) para\( x \in S \) y\( d(x, y) = 1 \) para distinto\( x, \, y \in S \) es una métrica en\( S \), conocida como la métrica discreta. Esta métrica genera la topología discreta.

Prueba

Claramente\( d(x, y) = 0 \) si y solo si\( x = y \), y\( d(x, y) = d(y, x) \) para\( x, \, y \in S \), así se mantienen las propiedades positivas y simétricas. Para la desigualdad triangular, supongamos\( x, \, y, \, z \in S \). La desigualdad se mantiene trivialmente si los puntos no son distintos. Si los puntos son distintos, entonces\( d(x, z) = 1 \) y\( d(x, y) + d(y, z) = 2 \).

En aplicaciones de probabilidad, la topología discreta suele ser apropiada cuando\( S \) es contable. Tenga en cuenta también que la métrica discreta es la distancia del gráfico si\( S \) se convierte en la gráfica completa, por lo que\( (x, y) \) es un borde para cada par de vértices distintos\( x, \, y \in S \).