CO-1: Describir los roles que la bioestadística desempeña en la disciplina de la salud pública.
A lo largo del curso, agregaremos a nuestra comprensión de las definiciones, conceptos y procesos que aquí se introducen. ¡No se espera que obtenga una comprensión completa de este proceso hasta mucho más tarde en el curso!
Para entender realmente cómo funciona este proceso, necesitamos ponerlo en un contexto. Eso lo haremos introduciendo una de las ideas centrales de este curso, el Panorama Grande de la Estadística.
Introduciremos el Big Picture construyéndolo gradualmente y explicando cada componente.
Al final de la explicación introductoria, una vez que tengas el Big Picture completo frente a ti, lo volveremos a mostrar usando un ejemplo concreto.
Objetivos de aprendizaje
LO 1.3: Identificar y diferenciar entre los componentes del panorama general de la estadística
El proceso de estadística inicia cuando identificamos a qué grupo queremos estudiar o aprender algo. Llamamos a este grupo la población.
Tenga en cuenta que la palabra “población” aquí (y en todo el curso) no sólo se usa para referirse a las personas; se usa en el sentido estadístico más amplio, donde la población puede referirse no sólo a las personas, sino también a los animales, cosas etc. Por ejemplo, podríamos estar interesados en:
- las opiniones de la población de adultos estadounidenses sobre la pena de muerte; o
- cómo reacciona la población de ratones a una determinada sustancia química; o
- el precio promedio de la población de todos los departamentos de una habitación en una ciudad determinada.
Nota
La población, entonces, es todo el grupo que es el blanco de nuestro interés.
En la mayoría de los casos, la población es tan grande que por mucho que queramos, no hay absolutamente ninguna manera de que podamos estudiarla todo (imagínese tratando de obtener las opiniones de todos los adultos estadounidenses sobre la pena de muerte...).
Un enfoque más práctico sería examinar y recolectar datos únicamente de un subgrupo de la población, al que llamamos muestra. Llamamos a este primer componente, que consiste en elegir una muestra y recolectar datos de ella, Producir datos.
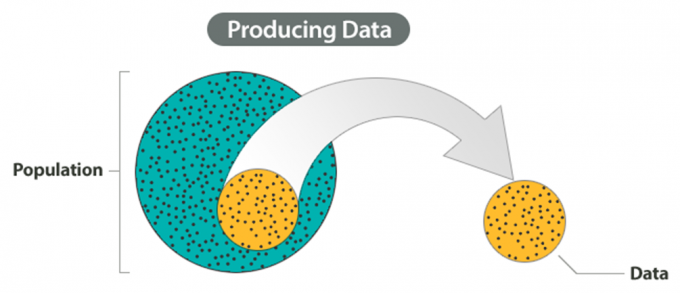
Nota
Una muestra es un subconjunto s de la población de la que recopilamos datos.
Cabe señalar que dado que, por razones prácticas, necesitamos comprometer y examinar sólo un subgrupo de la población en lugar de toda la población, debemos hacer un esfuerzo para elegir una muestra de tal manera que represente bien a la población.
Por ejemplo, si elegimos una muestra de la población de adultos estadounidenses, y preguntamos sus opiniones sobre un programa federal de salud en particular, no queremos que nuestra muestra consista solo por republicanos o solo demócratas.
Una vez recopilados los datos, lo que tenemos es una larga lista de respuestas a preguntas, o números, y para explorar y darle sentido a los datos, necesitamos resumir esa lista de manera significativa.
Este segundo componente, que consiste en resumir los datos recopilados, se denomina Análisis Exploratorio de Datos o Estadística Descriptiva.
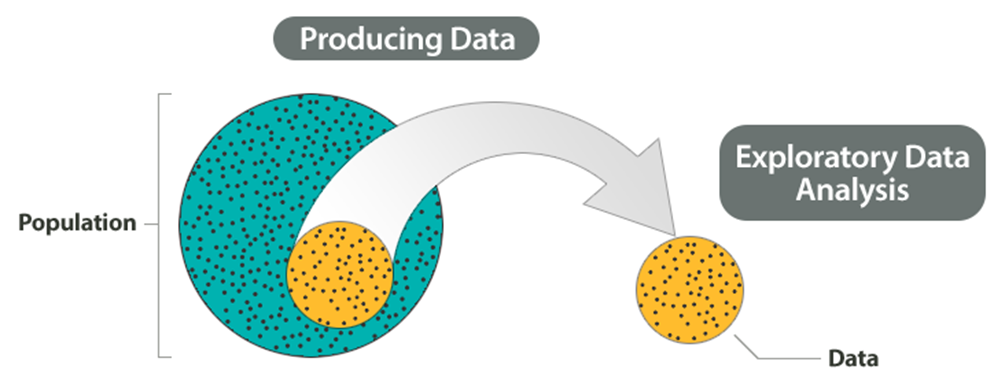
Ahora hemos obtenido los resultados de la muestra y los hemos resumido, pero no hemos terminado. Recuerde que nuestro objetivo es estudiar a la población, entonces lo que queremos es poder sacar conclusiones sobre la población a partir de los resultados de la muestra.
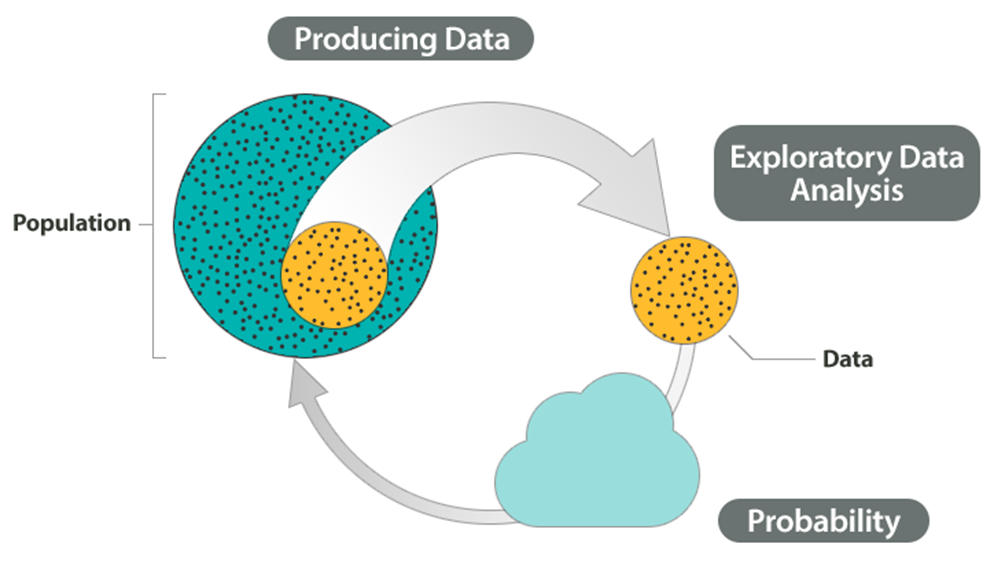
Antes de que podamos hacerlo, necesitamos ver cómo la muestra que estamos usando puede diferir de la población en su conjunto, para que podamos facetarlo en nuestro análisis. Para examinar esta diferencia, utilizamos Probabilidad, que es el tercer componente en el panorama general.
El tercer componente en el Panorama Grande de la Estadística, la probabilidad es en esencia la “maquinaria” que nos permite sacar conclusiones sobre la población a partir de los datos recopilados en la muestra.
Finalmente, podemos usar lo que hemos descubierto sobre nuestra muestra para sacar conclusiones sobre nuestra población.
Llamamos a este componente final en el proceso Inferencia.
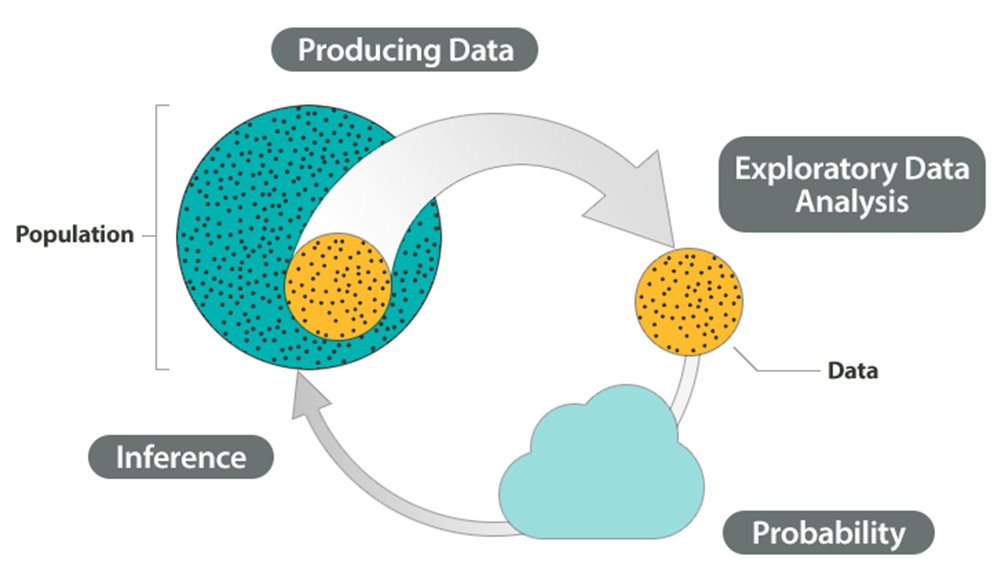
Este es el panorama general de la estadística.
EJEMPLO: Encuestas de opinión pública
A finales de abril de 2005, se realizó una encuesta (a cargo de ABC News y el Washington Post), con el propósito de conocer las opiniones de adultos estadunidenses sobre la pena de muerte.
1. Producir datos: Se eligió una muestra (representativa) de 1,082 adultos estadounidenses, y a cada adulto se le preguntó si favorecía o se opuso a la pena de muerte.
2. Análisis Exploratorio de Datos (EDA): Se resumieron los datos recopilados, y se encontró que 65% de los adultos muestreados favorecen la pena de muerte para las personas condenadas por homicidio.
3 y 4. Probabilidad e inferencia: Con base en el resultado de la muestra (de 65% favoreciendo la pena de muerte) y nuestro conocimiento de probabilidad, se concluyó (con 95% de confianza) que el porcentaje de quienes favorecen la pena de muerte en la población se encuentra dentro del 3% de lo que se obtuvo en la muestra (es decir, entre 62% y 68%). La siguiente figura resume el ejemplo:
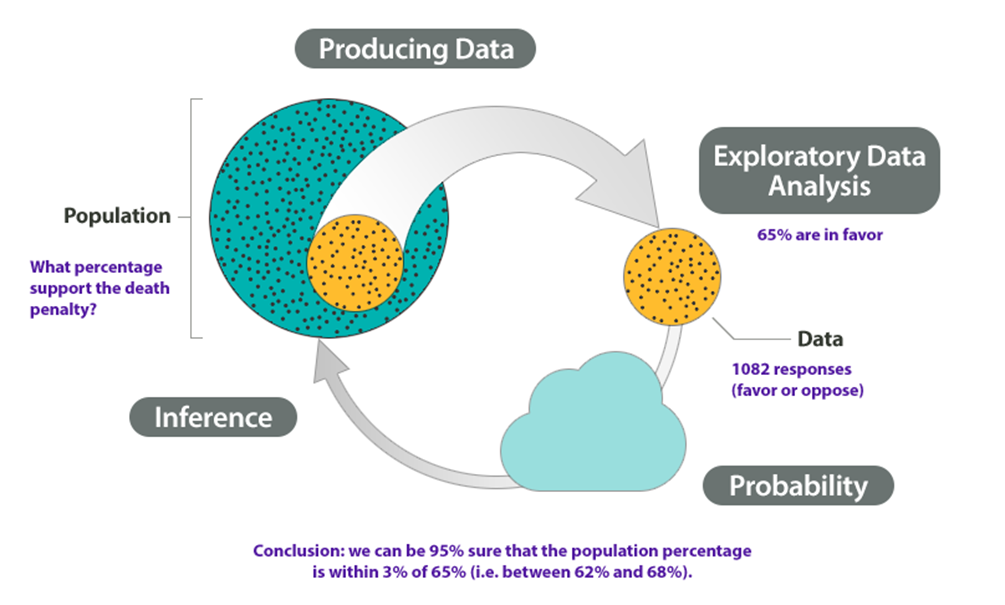
Estructura del Curso
La estructura de todo este curso se basa en el panorama general.
El curso contará con 4 unidades; una para cada uno de los componentes del panorama general.
Como muestra la siguiente figura, aunque sea el segundo en el proceso de estadística, iniciaremos este curso con análisis exploratorio de datos (EDA), continuaremos discutiendo la producción de datos, luego pasaremos a la probabilidad, para que al final podamos discutir la inferencia.
Las principales razones por las que comenzamos con EDA es que necesitamos entender lo suficiente sobre lo que queremos hacer con nuestros datos antes de poder discutir los temas relacionados con cómo recopilarlos!!
Esto también nos permite introducir muchos conceptos importantes al principio del curso para que tengas tiempo suficiente para dominarlos antes de que volvamos a la inferencia al final del curso.
En la siguiente figura se resume la estructura del curso.
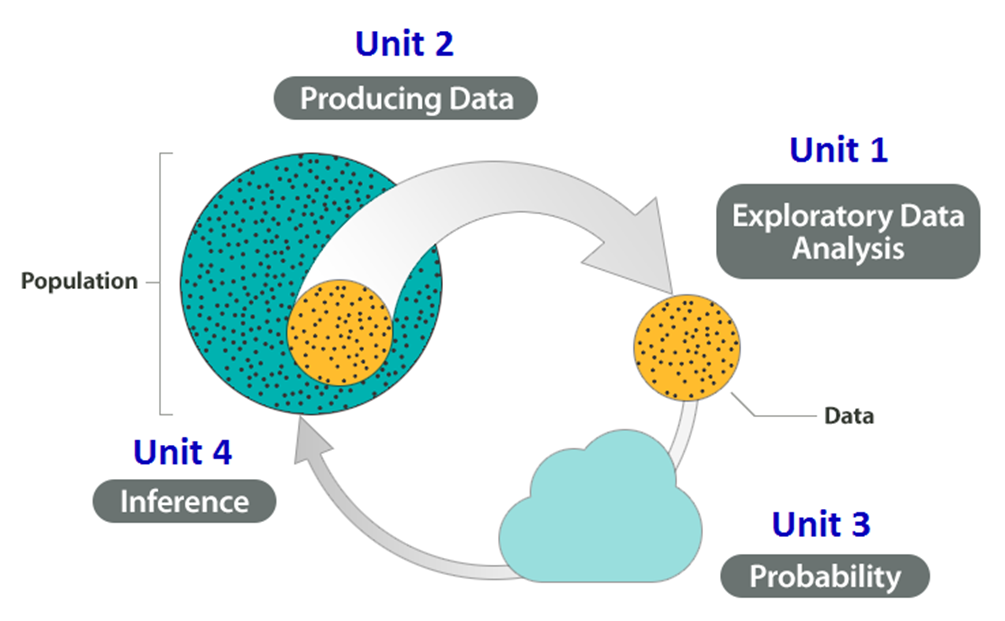
Como verás, el Big Picture es la base sobre la que se construye todo el curso, tanto conceptual como estructuralmente.
Nos referiremos a él a menudo, y tenerlo en mente te ayudará a medida que avanzas en el curso.








