Distribución de Muestreo de la Proporción Muestra, p-hat
- Última actualización
- Guardar como PDF
- Page ID
- 151219
CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.
Comportamiento de las proporciones muestrales
Objetivos de aprendizaje
LO 6.21: Aplicar la distribución muestral de la proporción muestral (cuando corresponda). En particular, poder identificar muestras inusuales de una población determinada.
Ejemplo 6: Comportamiento de las proporciones de la muestra
Aproximadamente el 60% de todos los estudiantes universitarios de medio tiempo en los Estados Unidos son mujeres. (Es decir, la proporción poblacional de mujeres entre los estudiantes universitarios de medio tiempo es p = 0.6.) ¿Qué esperarías ver en cuanto al comportamiento de una proporción muestral de hembras (p-hat) si se tomaran muestras aleatorias de talla 100 de la población de todos los estudiantes universitarios de medio tiempo?
Como vimos antes, debido a la variabilidad del muestreo, la proporción muestral en muestras aleatorias de tamaño 100 tomará valores numéricos que varían según las leyes del azar: en otras palabras, la proporción muestral es una variable aleatoria. Para resumir el comportamiento de cualquier variable aleatoria, nos enfocamos en tres características de su distribución: el centro, la propagación y la forma.
Basándonos únicamente en nuestra intuición, esperaríamos lo siguiente:
Centro: Algunas proporciones de muestra estarán en el lado bajo —digamos, 0.55 o 0.58— mientras que otras estarán en el lado alto —digamos, 0.61 o 0.66. Es razonable esperar que todas las proporciones de muestra en muestras aleatorias repetidas promedien a la proporción de población subyacente, 0.6. En otras palabras, la media de la distribución de p-hat debe ser p.
Difusión: Para muestras de 100, esperaríamos que las proporciones muestrales de hembras no se alejaran demasiado de la proporción poblacional 0.6. Las proporciones de la muestra inferiores a 0.5 o superiores a 0.7 serían bastante sorprendentes. Por otro lado, si solo tomáramos muestras de talla 10, no nos sorprendería en absoluto una proporción muestral de hembras incluso tan baja como 4/10 = 0.4, o tan alta como 8/10 = 0.8. Así, el tamaño de la muestra juega un papel en la dispersión de la distribución de la proporción muestral: debe haber menos dispersión para muestras más grandes, más dispersión para muestras más pequeñas.
Forma: Las proporciones de muestra más cercanas a 0.6 serían las más comunes, y las proporciones de muestra alejadas de 0.6 en cualquier dirección serían progresivamente menos probables. Es decir, la forma de la distribución de la proporción muestral debe abultarse en el medio y estrechar en los extremos: debe ser algo normal.
Comentario:
- La distribución de los valores de las proporciones muestrales (p-hat) en muestras repetidas (del mismo tamaño) se denomina distribución muestral de p-hat.
El propósito del siguiente video y actividad es verificar si nuestra intuición sobre el centro, la propagación y la forma de la distribución muestral de p-hat era correcta a través de simulaciones.
Video
Video: Simulación #1 (p-hat) (4:13)
¿Conseguí esto? : Simulación #1 (p-hat)
En este punto, tenemos un buen sentido de lo que sucede a medida que tomamos muestras aleatorias de una población. Nuestra simulación sugiere que nuestra intuición inicial sobre la forma y el centro de la distribución del muestreo es correcta. Si la población tiene una proporción de p, entonces muestras aleatorias del mismo tamaño extraídas de la población tendrán proporciones muestrales cercanas a p. Más específicamente, la distribución de proporciones muestrales tendrá una media de p.
También observamos que para esta situación, las proporciones muestrales son aproximadamente normales. Veremos más adelante que no siempre es así. Pero si las proporciones muestrales se distribuyen normalmente, entonces la distribución se centra en p.
Ahora queremos usar la simulación para ayudarnos a pensar más sobre la variabilidad que esperamos ver en las proporciones de la muestra. Nuestra intuición nos dice que las muestras más grandes se aproximarán mejor a la población, por lo que podríamos esperar menos variabilidad en muestras grandes.
En el próximo recorrido utilizaremos simulaciones para investigar esta idea. Después de ese recorrido, ataremos estas ideas a una teoría más formal.
Video
Video: Simulación #2 (p-hat) (4:55)
¿Conseguí esto? : Simulación #2 (p-hat)
Las simulaciones reforzaron lo que tiene sentido para nuestra intuición. Muestras aleatorias más grandes se aproximarán mejor a la proporción poblacional Cuando el tamaño de la muestra es grande, las proporciones de la muestra estarán más cerca de p. Es decir, la distribución de muestreo para muestras grandes tiene menor variabilidad. La teoría de probabilidad avanzada confirma nuestras observaciones y da una manera más precisa de describir la desviación estándar de las proporciones de la muestra. Esto se describe a continuación.
La distribución muestral de la proporción muestral
Si se toman muestras aleatorias repetidas de un tamaño dado n de una población de valores para una variable categórica, donde la proporción en la categoría de interés es p, entonces la media de todas las proporciones muestrales (p-hat) es la proporción poblacional (p).
En cuanto a la dispersión de todas las proporciones muestrales, la teoría dicta el comportamiento de manera mucho más precisa que decir que hay menos dispersión para muestras más grandes. De hecho, la desviación estándar de todas las proporciones de la muestra está directamente relacionada con el tamaño de la muestra, n como se indica a continuación.
![]()
Dado que el tamaño de muestra n aparece en el denominador de la raíz cuadrada, la desviación estándar disminuye a medida que aumenta el tamaño de la muestra. Finalmente, la forma de la distribución de p-hat será aproximadamente normal siempre y cuando el tamaño de muestra n sea lo suficientemente grande. La convención es exigir que tanto np como n (1 — p) sean al menos 10.
Podemos resumir todo lo anterior de la siguiente manera:
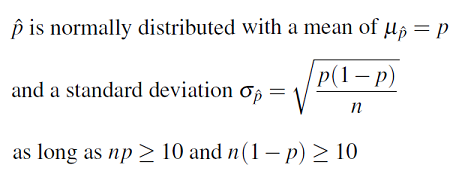
Apliquemos este resultado a nuestro ejemplo y veamos cómo se compara con nuestra simulación.
En nuestro ejemplo, n = 25 (tamaño de muestra) y p = 0.6. Nótese que np = 15 ≥ 10 y n (1 — p) = 10 ≥ 10. Por lo tanto, podemos concluir que p-hat es aproximadamente una distribución normal con media p = 0.6 y desviación estándar
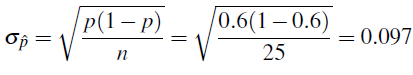
(que está muy cerca de lo que vimos en nuestra simulación).
Comentario:
- Estos resultados son similares a los de las variables aleatorias binomiales (X) discutidas anteriormente. Tenga cuidado de no confundir los resultados para la media y desviación estándar de X con los de p-hat.
Aprender haciendo: Distribución de muestreo de p-hat
¿Conseguí esto? : Distribución de muestreo de p-hat
Si una distribución de muestreo es normalmente conformada, entonces podemos aplicar la Regla de Desviación Estándar y usar puntuaciones z para determinar las probabilidades. Veamos algunos ejemplos.
EJEMPLO 7: Uso de la distribución de muestras de p-hat
Se toma una muestra aleatoria de 100 estudiantes de la población de todos los estudiantes de medio tiempo en Estados Unidos, para lo cual la proporción general de mujeres es de 0.6.
a) ¿Existe un 95% de probabilidad de que la proporción muestral (p-hat) caiga entre qué dos valores?
En primer lugar señalar que la distribución de p-hat tiene media p = 0.6, desviación estándar
\(\sigma_{\hat{p}}=\sqrt{\dfrac{p(1-p)}{n}}=\sqrt{\dfrac{0.6(1-0.6)}{100}}=0.05\)
y una forma cercana a lo normal, ya que np = 100 (0.6) = 60 y n (1 — p) = 100 (0.4) = 40 son ambos mayores que 10. Se aplica la Regla de Desviación Estándar: la probabilidad es aproximadamente 0.95 de que p-hat caiga dentro de 2 desviaciones estándar de la media, es decir, entre 0.6 — 2 (0.05) y 0.6 + 2 (0.05). Hay aproximadamente un 95% de probabilidad de que p-hat caiga en el intervalo (0.5, 0.7) para muestras de este tamaño.
b) ¿Cuál es la probabilidad de que la proporción muestral p-hat sea menor o igual a 0.56?
Para encontrar
\(P(\hat{p} \leq 0.56)\)
estandarizamos 0.56 en una puntuación z restando la media y dividiendo el resultado por la desviación estándar. Entonces podemos encontrar la probabilidad usando la calculadora normal estándar o tabla.
\(P(\hat{p} \leq 0.56)=P\left(Z \leq \dfrac{0.56-0.6}{0.05}\right)=P(Z \leq-0.80)=0.2119\)
Para ver el impacto del tamaño de la muestra en estos cálculos de probabilidad, considere la siguiente variación de nuestro ejemplo.
EJEMPLO 8: Uso de la distribución de muestras de p-hat
Se toma una muestra aleatoria de 2500 estudiantes de la población de todos los estudiantes de medio tiempo en Estados Unidos, para lo cual la proporción general de mujeres es de 0.6.
a) ¿Existe un 95% de probabilidad de que la proporción muestral (p-hat) caiga entre qué dos valores?
En primer lugar señalar que la distribución de p-hat tiene media p = 0.6, desviación estándar
\(\sigma_{\hat{p}}=\sqrt{\dfrac{p(1-p)}{n}}=\sqrt{\dfrac{0.6(1-0.6)}{2500}}=0.01\)
y una forma cercana a la normal, ya que np = 2500 (0.6) = 1500 y n (1 — p) = 2500 (0.4) = 1000 son ambos mayores que 10. Se aplica la Regla de Desviación Estándar: la probabilidad es aproximadamente 0.95 de que p-hat caiga dentro de 2 desviaciones estándar de la media, es decir, entre 0.6 — 2 (0.01) y 0.6 + 2 (0.01). Hay aproximadamente un 95% de probabilidad de que p-hat caiga en el intervalo (0.58, 0.62) para muestras de este tamaño.
b) ¿Cuál es la probabilidad de que la proporción muestral p-hat sea menor o igual a 0.56?
Para encontrar
\(P(\hat{p} \leq 0.56)\)
estandarizamos 0.56 a en una puntuación z restando la media y dividiendo el resultado por la desviación estándar. Entonces podemos encontrar la probabilidad usando la calculadora normal estándar o tabla.
\(P(\hat{p} \leq 0.56)=P\left(Z \leq \dfrac{0.56-0.6}{0.01}\right)=P(Z \leq-4) \approx 0\)
Comentario:
- Siempre y cuando la muestra sea verdaderamente aleatoria, la distribución de p-hat se centra en p, sin importar el tamaño de la muestra que se haya tomado. Las muestras más grandes tienen menos dispersión. Específicamente, cuando multiplicamos el tamaño de la muestra por 25, aumentándolo de 100 a 2,500, la desviación estándar se redujo a 1/5 de la desviación estándar original. La proporción muestral se aleja menos de la proporción poblacional 0.6 cuando la muestra es mayor: tiende a caer entre 0.5 y 0.7 para muestras de tamaño 100, mientras que tiende a caer entre 0.58 y 0.62 para muestras de tamaño 2,500. No es tan improbable tomar un valor tan bajo como 0.56 para muestras de 100 (la probabilidad es superior al 20%) pero es casi imposible tomar un valor tan bajo como 0.56 para muestras de 2,500 (la probabilidad es prácticamente cero).
Applet: Distribución de muestreo para una proporción de muestra

