Resumen (Unidad 3B - Distribuciones de Muestreo)
- Última actualización
-
-
Guardar como PDF
Finalmente hemos llegado al final de nuestra discusión de probabilidad con nuestra discusión de distribuciones de muestreo, que se puede ver de dos maneras. Por un lado, las Distribuciones de Muestreo pueden verse como un caso especial de Variables Aleatorias ya que discutimos dos variables aleatorias especiales: la media muestral (x-bar) y la proporción muestral (p-hat). Por otro lado, las Distribuciones de Muestreo pueden verse como el puente que nos lleva de la probabilidad a la inferencia estadística.
Como se mencionó en la introducción, este último concepto en probabilidad es el puente entre la sección de probabilidad y la inferencia. Se centra en la relación entre los valores de la muestra (estadística) y los valores poblacionales (parámetros). Las estadísticas varían de una muestra a otra debido a la variabilidad del muestreo y, por lo tanto, pueden considerarse como variables aleatorias cuya distribución llamamos distribución de muestreo.
En nuestra discusión sobre las distribuciones de muestreo, nos centramos en dos estadísticas, la proporción muestral, p-hat y la media muestral, barra x. Nuestro objetivo fue explorar la distribución muestral de estas dos estadísticas en relación con sus respectivos parámetros poblacionales, p y μ (mu), y encontramos en ambos casos que bajo ciertas condiciones la distribución muestral es aproximadamente normal. Este resultado se conoce como el Teorema del Límite Central. Como veremos en la siguiente sección, el Teorema del Límite Central es la base para la inferencia estadística.
Distribuciones de Muestreo
Un parámetro es un número que describe la población, y un estadístico es un número que describe la muestra.
- Los parámetros son fijos, y en la práctica, generalmente desconocidos.
- Las estadísticas cambian de muestra a muestra debido a la variabilidad del muestreo.
- El comportamiento de los posibles valores que el estadístico puede tomar en muestras repetidas se denomina distribución muestral de ese estadístico.
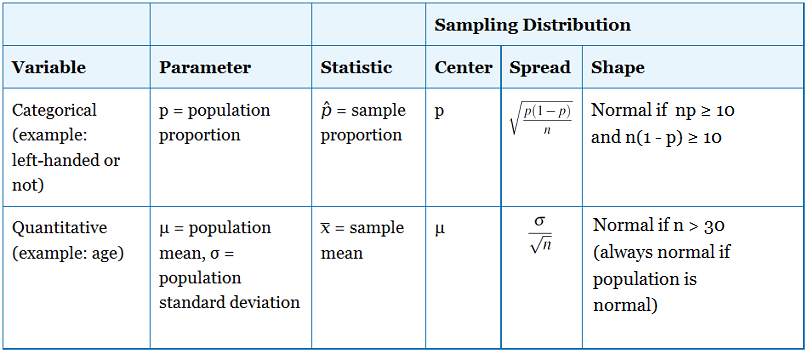
- La siguiente tabla resume la información importante sobre las dos distribuciones de muestreo que cubrimos. Ambos resultados se derivan del teorema del límite central que básicamente establece que a medida que aumenta el tamaño de la muestra, la distribución del promedio a partir de una muestra de tamaño n se distribuye cada vez más normalmente.