Variables aleatorias binomiales
- Última actualización
- Guardar como PDF
- Page ID
- 151235
CO-6: Aplicar conceptos básicos de probabilidad, variación aleatoria y distribuciones de probabilidad estadística de uso común.
Reseña:
Vídeo: Variables Aleatorias Binomiales (12:52)
Hasta ahora, en nuestra discusión sobre las variables aleatorias discretas, se nos ha presentado a:
- La distribución de probabilidad, que nos dice qué valores toma una variable, y con qué frecuencia los toma.
- La media de la variable aleatoria, que nos indica el valor promedio a largo plazo que toma la variable aleatoria.
- La desviación estándar de la variable aleatoria, que nos indica una distancia típica (o promedio a largo plazo) entre la media de la variable aleatoria y los valores que toma.
Ahora vamos a introducir una clase especial de variables aleatorias discretas que son muy comunes, porque como verás, surgirán en muchas situaciones — variables aleatorias binomiales.
Así es como presentaremos este material.
- Primero, explicaremos qué tipo de experimentos aleatorios dan lugar a una variable aleatoria binomial, y cómo se define la variable aleatoria binomial en esos tipos de experimentos.
- Luego presentaremos la distribución de probabilidad de la variable aleatoria binomial, que se presentará como una fórmula, y explicaremos por qué la fórmula tiene sentido.
- Concluiremos nuestra discusión presentando la media y desviación estándar de la variable binomial aleatoria.
Como acabamos de mencionar, comenzaremos describiendo qué tipo de experimentos aleatorios dan lugar a una variable aleatoria binomial. Llamaremos a este tipo de experimento aleatorio un “experimento binomial”.
Experimento binomial
Objetivos de aprendizaje
LO 6.14: En su caso, aplicar el modelo binomial para encontrar probabilidades.
Los experimentos binomiales son experimentos aleatorios que consisten en un número fijo de ensayos repetidos, como lanzar una moneda 10 veces, elegir aleatoriamente a 10 personas, rodar un dado 5 veces, etc.
Estos ensayos, sin embargo, deben ser independientes en el sentido de que el resultado en un ensayo no tiene efecto sobre el resultado en otros ensayos.
En cada uno de estos ensayos repetidos hay un resultado que nos interesa (llamamos a este resultado “éxito”), y cada uno de los ensayos es idéntico en el sentido de que la probabilidad de que el juicio termine en un “éxito” es la misma en cada uno de los ensayos.
Entonces, por ejemplo, si nuestro experimento está echando una moneda 10 veces, y nos interesa el resultado “cabezas” (nuestro “éxito”), entonces este será un experimento binomial, ya que los 10 ensayos son independientes, y la probabilidad de éxito es 1/2 en cada uno de los 10 ensayos.
Resumamos y demos más ejemplos.
Los requisitos para que un experimento aleatorio sea un experimento binomial son:
- un número fijo (n) de ensayos
- cada juicio debe ser independiente de los demás
- cada ensayo tiene solo dos resultados posibles, llamados “éxito” (el resultado de interés) y “fracaso”
- hay una probabilidad constante (p) de éxito para cada ensayo, cuyo complemento es la probabilidad (1 — p) de fracaso, a veces denotada como q = (1 — p)
En experimentos binomiales aleatorios, el número de éxitos en n ensayos es aleatorio.
Puede ser tan bajo como 0, si todos los ensayos terminan en fracaso, o tan alto como n, si todos los n ensayos terminan en éxito.
La variable aleatoria X que representa el número de éxitos en esos n ensayos se denomina variable aleatoria binomial, y está determinada por los valores de n y p. Decimos, “X es binomial con n =... y p =...”
EJEMPLO: Experimentos aleatorios (¿binomiales o no?)
Consideremos algunos experimentos aleatorios.
En cada una de ellas, decidiremos si la variable aleatoria es binomial. Si es así, determinaremos los valores para n y p. Si no lo es, explicaremos por qué no.
Ejemplo A:
Una moneda justa es volteada 20 veces; X representa el número de cabezas.
X es binomial con n = 20 y p = 0.5.
Ejemplo B:
Enrolla un dado justo 50 veces; X es el número de veces que obtienes un seis.
X es binomial con n = 50 y p = 1/6.
Ejemplo C:
Enrolle un dado justo repetidamente; X es el número de rollos que se necesita para obtener un seis.
X no es binomial, porque el número de ensayos no es fijo.
Ejemplo D:
Dibuja 3 cartas al azar, una tras otra, sin reemplazo, de un conjunto de 4 cartas que consta de un palo, un diamante, un corazón y una pala; X es el número de diamantes seleccionados.
X no es binomial, porque las selecciones no son independientes. (La probabilidad (p) de éxito no es constante, porque se ve afectada por selecciones anteriores.)
Ejemplo E:
Dibuja 3 cartas al azar, una tras otra, con reemplazo, de un juego de 4 cartas que consta de un palo, un diamante, un corazón y una pala; X es el número de diamantes seleccionados. Muestreo con reemplazo asegura independencia.
X es binomial con n = 3 y p = 1/4
Ejemplo F:
Aproximadamente 1 de cada 20 niños tiene cierta enfermedad. Sea X el número de niños con la enfermedad de una muestra aleatoria de 100 niños. Aunque los niños son muestreados sin reemplazo, se supone que estamos muestreando de una población tan vasta que las selecciones son prácticamente independientes.
X es binomial con n = 100 y p = 1/20 = 0.05.
Ejemplo G:
La probabilidad de tener el tipo de sangre B es de 0.1. Elige 4 personas al azar; X es el número con el tipo de sangre B.
X es binomial con n = 4 y p = 0.1.
Ejemplo H:
Un alumno responde 10 preguntas del cuestionario completamente al azar; las primeras cinco son verdaderas/falsas, las segundas cinco son de opción múltiple, con cuatro opciones cada una. X representa el número de respuestas correctas.
X no es binomial, porque p cambia de 1/2 a 1/4.
Comentarios:
- El Ejemplo D anterior no fue binomial porque el muestreo sin reemplazo resultó en selecciones dependientes.
- En particular, la probabilidad de que la segunda carta sea un diamante depende mucho de si la primera carta fue o no un diamante:
- la probabilidad es 0 si la primera carta era un diamante, 1/3 si la primera carta no era un diamante.
- En contraste, el Ejemplo E fue binomial porque el muestreo con reemplazo resultó en selecciones independientes:
- la probabilidad de que cualquiera de las 3 cartas sea un diamante es 1/4 sin importar cuáles hayan sido las selecciones anteriores.
- Por otro lado, cuando se toma una muestra aleatoria relativamente pequeña de sujetos de una población grande, aunque el muestreo sea sin reemplazo, podemos asumir independencia porque el efecto matemático de eliminar a un individuo de una población muy grande en la siguiente selección es despreciable.
- Por ejemplo, en el Ejemplo F, se muestrearon 100 niños de la población de todos los niños.
- A pesar de que muestreamos a los niños sin reemplazo, si un niño tiene la enfermedad o no realmente no tiene ningún efecto sobre si otro niño tiene la enfermedad o no.
- Lo mismo es cierto para Ejemplo (G.) .
¿Conseguí esto? : ¿Binomial o no?
Distribución de probabilidad binomial — Uso de reglas de probabilidad
Ahora que entendemos lo que es una variable aleatoria binomial, y cuando surge, es el momento de discutir su distribución de probabilidad. Empezaremos con un ejemplo sencillo y luego generalizaremos a una fórmula.
EJEMPLO: Baraja de cartas
Considera una baraja regular de 52 cartas, en la que hay 13 cartas de cada palo: corazones, diamantes, palos y espadas. Seleccionamos 3 tarjetas al azar con reemplazo. Que X sea el número de tarjetas de diamante que obtuvimos (de las 3).
Tenemos 3 ensayos aquí, y son independientes (ya que la selección es con reemplazo). El resultado de cada ensayo puede ser éxito (diamante) o fracaso (no diamante), y la probabilidad de éxito es 1/4 en cada uno de los ensayos.
X, entonces, es binomial con n = 3 y p = 1/4.
Construyamos la distribución de probabilidad de X como hicimos en el capítulo sobre distribuciones de probabilidad. Recordemos que comenzamos con una mesa en la que:
- registrar todos los resultados posibles en 3 selecciones, donde cada selección puede resultar en éxito (un diamante, D) o fracaso (un no diamante, N).
- encontrar el valor de X que corresponde a cada resultado.
- utilizar principios de probabilidad simples para encontrar la probabilidad de cada resultado.
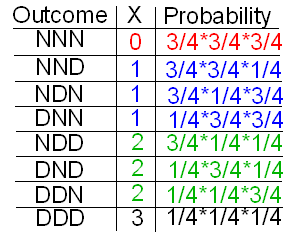
Con la ayuda del principio de adición, condensamos la información en esta tabla para construir la tabla de distribución de probabilidad real:
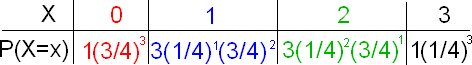
Para establecer una fórmula general para la probabilidad de que una variable aleatoria binomial X tome cualquier valor dado x, buscaremos patrones en la distribución anterior. Por la forma en que construimos esta distribución de probabilidad, sabemos que, en general:
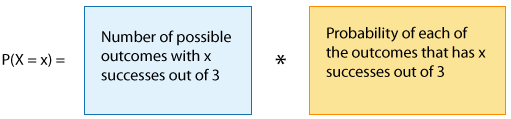
Empecemos con la segunda parte, la probabilidad de que haya x éxitos de 3, donde la probabilidad de éxito es 1/4.
Observe que las fracciones multiplicadas en cada caso son para la probabilidad de x éxitos (donde cada éxito tiene una probabilidad de p = 1/4) y las fallas restantes (3 — x) (donde cada falla tiene probabilidad de 1 — p = 3/4).
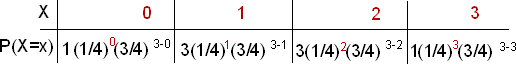
Entonces, en general:
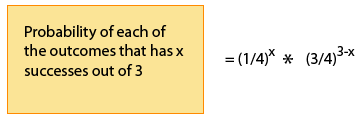
Pasemos a hablar sobre el número de posibles resultados con x éxitos de tres. Aquí es más difícil ver el patrón, así que daremos el siguiente resultado matemático.
Contar resultados
Considera un experimento aleatorio que consiste en n ensayos, cada uno terminando en éxito o fracaso. El número de posibles resultados en el espacio muestral que tienen exactamente k éxitos de n es:
\ (\ left (\ begin {array} {l}
n\\
k
\ end {array}\ right) =\ dfrac {n!} {k! (n-k)!} \)
La notación de la izquierda suele leerse como “n elige k”. Tenga en cuenta que n! se lee “n factorial” y se define como el producto 1 * 2 * 3 *... * n. 0! se define como 1.
EJEMPLO: Piercings
Eliges a 12 estudiantes universitarios masculinos al azar y registras si tienen algún piercing en las orejas (éxito) o no. Hay muchos resultados posibles de este experimento (¡en realidad, 4,096 de ellos!).
¿En cuántos de los posibles resultados de este experimento hay exactamente 8 éxitos (estudiantes que tienen al menos una oreja perforada)?
No hay manera de que empecemos a enumerar todos estos posibles resultados. El resultado anterior viene a nuestro rescate.
El resultado dice que en un experimento como este, donde repites un ensayo n veces (en nuestro caso, lo repetimos n = 12 veces, una vez por cada alumno que elegimos), el número de resultados posibles con exactamente 8 éxitos (de 12) es:
\(\dfrac{12!}{8!(12-8)!} = \dfrac{1*2*3*\cdots*12}{(1*2*3*\cdots*8)(1*2*3*4)} = 495\)
¿Conseguí esto? : Contar resultados
EJEMPLO: Tarjeta revisitada
Volvamos a nuestro ejemplo, en el que tenemos n = 3 pruebas (seleccionando 3 cartas). Vimos que hubo 3 posibles resultados con exactamente 2 éxitos de 3. El resultado lo confirma ya que:
\(\dfrac{3!}{2!(3-2)!} = \dfrac{1*2*3}{(1*2)(1)} = \dfrac{6}{2} = 3\)
En general, entonces
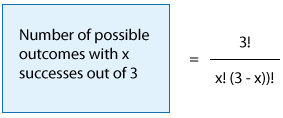
Poniéndolo todo junto, obtenemos que la distribución de probabilidad de X, que es binomial con n = 3 y p = 1/4 i
\(P(X=x)=\dfrac{3 !}{\mathrm{x} !(3-x) !}\left(\dfrac{1}{4}\right)^{x}\left(\dfrac{3}{4}\right)^{3-x} \quad x=0,1,2,3\)
En general, el número de formas de obtener x éxitos (y n — x fracasos) en n ensayos es
\ (\ left (\ begin {array} {l}
n\\
k
\ end {array}\ right) =\ dfrac {n!} {k! (n-k)!} \)
Por lo tanto, la probabilidad de x éxitos (y n — x fracasos) en n ensayos, donde la probabilidad de éxito en cada ensayo es p (y la probabilidad de fracaso es 1 — p) es igual al número de resultados en los que hay x éxitos de n ensayos, veces la probabilidad de x éxitos, veces la probabilidad de x éxitos, veces la probabilidad de n — x fallas:
Fórmula de probabilidad binomial para P (X = x)
\(P(X=x)=\dfrac{n !}{x !(n-x) !} p^{x}(1-p)^{(n-x)}\)
donde x puede tomar cualquier valor 0, 1,..., n.
Veamos otro ejemplo:
EJEMPLO: Tipo de sangre A
La probabilidad de tener el tipo sanguíneo A es de 0.4. Elige 4 personas al azar y deja que X sea el número con el tipo de sangre A.
X es una variable aleatoria binomial con n = 4 y p = 0.4.
Como revisión, primero vamos a encontrar la distribución de probabilidad de X a lo largo: construir una tabla provisional de todos los resultados posibles en S, los valores correspondientes de X y probabilidades. Luego construya la tabla de distribución de probabilidad para X.
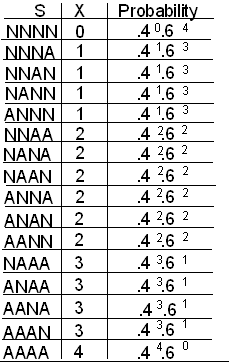
Como es habitual, la regla de suma nos permite combinar probabilidades para cada valor posible de X:

Ahora vamos a aplicar la fórmula para la distribución de probabilidad de una variable aleatoria binomial, y veamos que al usarla, obtenemos exactamente lo que conseguimos en el largo camino.
Recordemos que la fórmula general para la distribución de probabilidad de una variable aleatoria binomial con n ensayos y probabilidad de éxito p es:
\(P(X=x)=\dfrac{n !}{x !(n-x) !} p^{x}(1-p)^{(n-x)} \text { for } \mathrm{x}=0,1,2,3, \ldots, \mathrm{n}\)
En nuestro caso, X es una variable aleatoria binomial con n = 4 y p = 0.4, por lo que su distribución de probabilidad es:
\(P(X=x)=\dfrac{4 !}{x !(4-x) !}(0.4)^{x}(0.6)^{4-x} \text { for } \mathrm{x}=0,1,2,3,4\)
Usemos esta fórmula para encontrar P (X = 2) y ver que obtenemos exactamente lo que obtuvimos antes.
\(P(X=2)=\dfrac{4 !}{2 !(4-2) !}(0.4)^{2}(0.6)^{4-2}=\dfrac{1^{*} 2^{*} 3^{*} 4}{\left(1^{*} 2\right)\left(1^{*} 2\right)}(0.4)^{2}(0.6)^{2}=0.3456\)
Aprende haciendo: Probabilidades Binomiales (Usando Calculadora en Línea)
Ahora veamos algunas aplicaciones verdaderamente prácticas de variables aleatorias binomiales.
EJEMPLO: Vuelos aéreos
Estudios anteriores han demostrado que el 90% de los pasajeros reservados realmente llegan para un vuelo. Supongamos que un pequeño avión lanzadera tiene 45 asientos. Supondremos que los pasajeros llegan independientemente unos de otros. (Esta suposición no es realmente precisa, ya que no todas las personas viajan solas, sino que la usaremos para los fines de nuestro experimento).
Muchas veces las aerolíneas “sobrereservan” vuelos. Esto significa que la aerolínea vende más boletos que asientos en el avión. Esto se debe a que a veces los pasajeros no se presentan, y el avión debe volarse con asientos vacíos. No obstante, si hacen overbook, corren el riesgo de tener más pasajeros que asientos. Entonces, algunos pasajeros pueden estar infelices. También tienen el gasto extra de poner a esos pasajeros en otro vuelo y posiblemente suministrar hospedaje.
Con estos riesgos en mente, la aerolínea decide vender más de 45 boletos. Si desean mantener la probabilidad de que más de 45 pasajeros se presenten para subir al vuelo a menos de 0.05, ¿cuántos boletos deberían vender?
Se trata de una variable binomial aleatoria que representa el número de pasajeros que se presentan para el vuelo. Tiene p = 0.90, y n por determinar.
Supongamos que la aerolínea vende 50 boletos. Ahora tenemos n = 50 y p = 0.90. Queremos saber P (X > 45), que es 1 — P (X ≤ 45) = 1 — 0.57 o 0.43. Obviamente, no se mostraron todos los detalles de este cálculo, ya que se utilizó un paquete de tecnología estadística para calcular la respuesta. Esto es sin duda más de 0.05, por lo que la aerolínea debe vender menos asientos.
Si reducimos el número de boletos vendidos, deberíamos poder reducir esta probabilidad. Hemos calculado las probabilidades en la siguiente tabla:
| # boletos vendidos | P (X > 45) |
|---|---|
| 50 | 45)” class="lt-socialsci-152767">0.43 |
| 49 | 45)” class="lt-socialsci-152767">0.26 |
| 48 | 45)” class="lt-socialsci-152767">0.13 |
| 47 | 45)” class="lt-socialsci-152767">0.04 |
| 46 | 45)” class="lt-socialsci-152767">0.008 |
De esta tabla, podemos ver que al vender 47 boletos, la aerolínea puede reducir la probabilidad de que tenga más pasajeros presentados que asientos a menos del 5%.
Nota: Para practicar en la búsqueda de probabilidades binomiales, es posible que desee verificar uno o más de los resultados de la tabla anterior.
Aprender haciendo: Aplicación binomial
Media y Desviación Estándar de la Variable Aleatoria Binomial
Objetivos de aprendizaje
LO 6.15: Encuentra la media, varianza y desviación estándar de una variable binomial aleatoria.
Ahora que entendemos cómo encontrar probabilidades asociadas a una variable aleatoria X que es binomial, utilizando ya sea su fórmula de distribución de probabilidad o software, estamos listos para hablar sobre la media y desviación estándar de una variable aleatoria binomial. Empecemos con un ejemplo:
EJEMPLO: Tipo de sangre B - Media
En general, la proporción de personas con tipo de sangre B es de 0.1. Es decir, aproximadamente el 10% de la población tiene el tipo de sangre B.
Supongamos que tomamos muestras de 120 personas al azar. En promedio, ¿cuántos esperarías tener el tipo de sangre B?
La respuesta, 12, parece obvia; automáticamente, multiplicarías el número de personas, 120, por la probabilidad de tipo sanguíneo B, 0.1.
Esto sugiere la fórmula general para encontrar la media de una variable aleatoria binomial:
Reclamación:
Si X es binomial con los parámetros n y p, entonces el valor medio o esperado de X es:
\(\mu_X = np\)
Si bien la fórmula para la media es bastante intuitiva, no es en absoluto evidente cuál debería ser la varianza y desviación estándar. Resulta que:
Reclamación:
La ley de gas ideal es fácil de recordar y aplicar en la resolución de problemas, siempre y cuando se obtengan los valores adecuados a Si X es binomial con parámetros n y p, entonces la varianza y desviación estándar de X son:
\ begin {alineado}
\ sigma_ {X} ^ {2} &=n p (1-p)\
\ sigma_ {X} &=\ sqrt {n p (1-p)}
\ end {alineado}
Comentarios:
- La media binomial y varianza son casos especiales de nuestras fórmulas generales para la media y varianza de cualquier variable aleatoria. Claramente es mucho más sencillo usar las fórmulas de “atajo” presentadas anteriormente de lo que sería calcular la media y varianza o desviación estándar desde cero.
- Recuerda, estas fórmulas de “atajo” solo se mantienen en los casos en los que tienes una variable aleatoria binomial.
EJEMPLO: Tipo sanguíneo B - Desviación estándar
Supongamos que tomamos muestras de 120 personas al azar. El número con el tipo de sangre B debe ser aproximadamente 12, dar o tomar ¿cuántos? Es decir, ¿cuál es la desviación estándar del número X que tienen el tipo de sangre B?
Dado que n = 120 y p = 0.1,
\(\sigma_{X}^{2}=120(0.1)(1-0.1)=10.8 ; \quad \sigma_{X}=\sqrt{10.8} \approx 3.3\)
En una muestra aleatoria de 120 personas, debemos esperar que haya alrededor de 12 con tipo de sangre B, dar o tomar alrededor de 3.3.
¿Conseguí esto? : Distribución binomial
Antes de pasar a las variables aleatorias continuas, investiguemos la forma de las distribuciones binomiales.
Aprender haciendo: Formas de distribuciones binomiales

