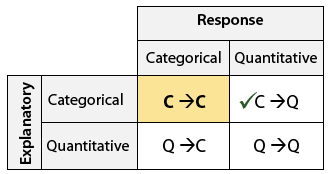
Caso C→C
- Page ID
- 151237
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
Introducción
Muestras Independientes (Solo Énfasis) |
Muestras dependientes (no discutidas) |
| Pruebas estándar
|
Prueba estándar
|
Mesas RxC
| Sin Diabetes | Pre-Diabetes | Diabetes | Total | |
| Bajo peso | 100 | |||
| Normal | 400 | |||
| Sobrepeso | 300 | |||
| Obesos | 200 | |||
| Total | 700 | 200 | 100 | 1000 |
| Sin Diabetes | Pre-Diabetes | Diabetes | Total | |
| Bajo peso | 100 (0.7) = 70 | 100 | ||
| Normal | 400 (0.7) = 280 | 400 | ||
| Sobrepeso | 300 (0.7) = 210 | 300 | ||
| Obesos | 200 (0.7) = 140 | 200 | ||
| Total | 700 | 200 | 100 | 1000 |
| Sin Diabetes | Pre-Diabetes | Diabetes | Total | |
| Bajo peso | 70 | 100 (0.2) = 20 | 100 (0.1) = 10 | 100 |
| Normal | 280 | 400 (0.2) = 80 | 400 (0.1) = 40 | 400 |
| Sobrepeso | 210 | 300 (0.2) = 60 | 300 (0.1) = 30 | 300 |
| Obesos | 140 | 200 (0.2) = 40 | 200 (0.1) = 20 | 200 |
| Total | 700 | 200 | 100 | 1000 |
| Sin Diabetes | Pre-Diabetes | Diabetes | Total | |
| Bajo peso | 70 | 20 | 10 | 100 |
| Normal | 280 | 80 | 40 | 400 |
| Sobrepeso | 210 | 60 | 30 | 300 |
| Obesos | 140 | 40 | 20 | 200 |
| Total | 700 | 200 | 100 | 1000 |
| Sin Diabetes | Pre-Diabetes | Diabetes | Total | |
| Bajo peso | 65 (70) | 22 (20) | 13 (10) | 100 |
| Normal | 285 (280) | 78 (80) | 37 (40) | 400 |
| Sobrepeso | 216 (210) | 53 (60) | 31 (30) | 300 |
| Obesos | 134 (140) | 47 (40) | 19 (20) | 200 |
| Total | 700 | 200 | 100 | 1000 |
| Sin Diabetes | Pre-Diabetes | Diabetes | Total | |
| Bajo peso | 90 (70) 90% |
7 (20) 7% |
3 (10) 3% |
100 |
| Normal | 340 (280) 85% |
40 (80) 10% |
20 (40) 5% |
400 |
| Sobrepeso | 180 (210) 60% |
90 (60) 30% |
30 (30) 10% |
300 |
| Obesos | 90 (140) 45% |
63 (40) 31.5% |
47 (20) 23.5% |
200 |
| Total | 700 | 200 | 100 | 1000 |
Mesas 2×2
| Sin Mejoras | Mejora | Total | |
| Control | 100 | ||
| Tratamiento | 100 | ||
| Total | 120 | 80 | 200 |
| Sin Mejoras | Mejora | Total | |
| Control | 100 (0.6) = 60 | 100 (0.4) = 40 | 100 |
| Tratamiento | 100 (0.6) = 60 | 100 (0.4) = 40 | 100 |
| Total | 120 | 80 | 200 |
| Sin Mejoras | Mejora | Total | |
| Control | 80 | 20 | 100 |
| Tratamiento | 40 | 60 | 100 |
| Total | 120 | 80 | 200 |
Prueba de Chi-cuadrado para la independencia
Alternativa no paramétrica: Prueba Exacta de Fisher
| Variable explicativa | ¿Qué Prueba es Apropiada? | Valor P | Decisión |
| CARRERA | Mín. Recuento esperado = 8.12 Mesa 3×2 Usar Chi-cuadrado Pearson (desde RxC) |
0.0819 (Chi-cuadrado — SAS) 0.082 (Chi-cuadrado — SPSS) |
No Rechazar Ho |
| HUMO | Mín. Recuento esperado = 23.1 Tabla 2×2 Corrección de Continuidad de Uso (desde 2×2) |
0.040 (Corrección de Continuidad — SPSS) 0.0396 (Continuidad Adj — SAS) |
Rechazar Ho |
| PTL | Mín. Recuento esperado = 0.31 4×2 tabla La prueba exacta de Fisher es más apropiada |
3.106 E-04 = 0.0003106 (Fisher's — SAS) 0.000 (Fisher's — SPSS) 0.0008 (Chi-cuadrado — SAS) 0.001 (Chi-cuadrado — SPSS) |
Rechazar Ho |
| HT | Mín. Recuento esperado = 3.75 2×2 tabla La prueba exacta de Fisher puede ser más apropiada |
0.0516 (Fisher's — SAS) 0.052 (Fisher's — SPSS) |
No Rechazar a Ho (Apenas) |
| UI | Mín. Recuento esperado = 8.74 Tabla 2×2 Corrección de Continuidad de Uso |
0.0355 (Continuidad Adj. — SAS) 0.035 (Corrección de Continuidad — SPSS) |
Rechazar Ho |
| Variable explicativa | Comparación de los porcentajes condicionales de bajo peso al nacer |
| CARRERA | Carrera = Blancas: 23.96% Carrera = Negro: 42.31% Carrera = Otro: 37.31% |
| HUMO | Humo = No: 25.22% Humo = Si: 40.54% |
| PTL | Historia de Trabajo Prematuro = 0:25.79% Historia de Trabajo Prematuro = 1:66.67% Historia de Trabajo Prematuro = 2:40.00% (Tenga en cuenta tamaño de muestra pequeño de 5 para esta fila) Historia de Trabajo Prematuro = 3:0.00% (Nota tamaño de muestra pequeño de 1 para esta fila) |
| HT | Hipertensión = No: 29.38% Hipertensión = Sí: 58.33% (Tenga en cuenta el tamaño de muestra pequeño de 12 para esta fila) |
| UI | Presencia de irritabilidad uterina = No: 27.95% Presencia de irritabilidad uterina = Sí: 50.00% |