6.2: Una introducción al trazado
- Page ID
- 151871
Antes de discutir cualquier gráfica especializada, comencemos dibujando algunas gráficas muy simples solo para tener una idea de lo que es dibujar imágenes usando R. Para ello, vamos a crear un pequeño vector Fibonacci que contenga algunos números que nos gustaría que R dibuje para nosotros. Entonces, le pediremos a R que trazar () esos números:
> Fibonacci <- c( 1,1,2,3,5,8,13 )
> plot( Fibonacci )El resultado es la Figura 6.2.
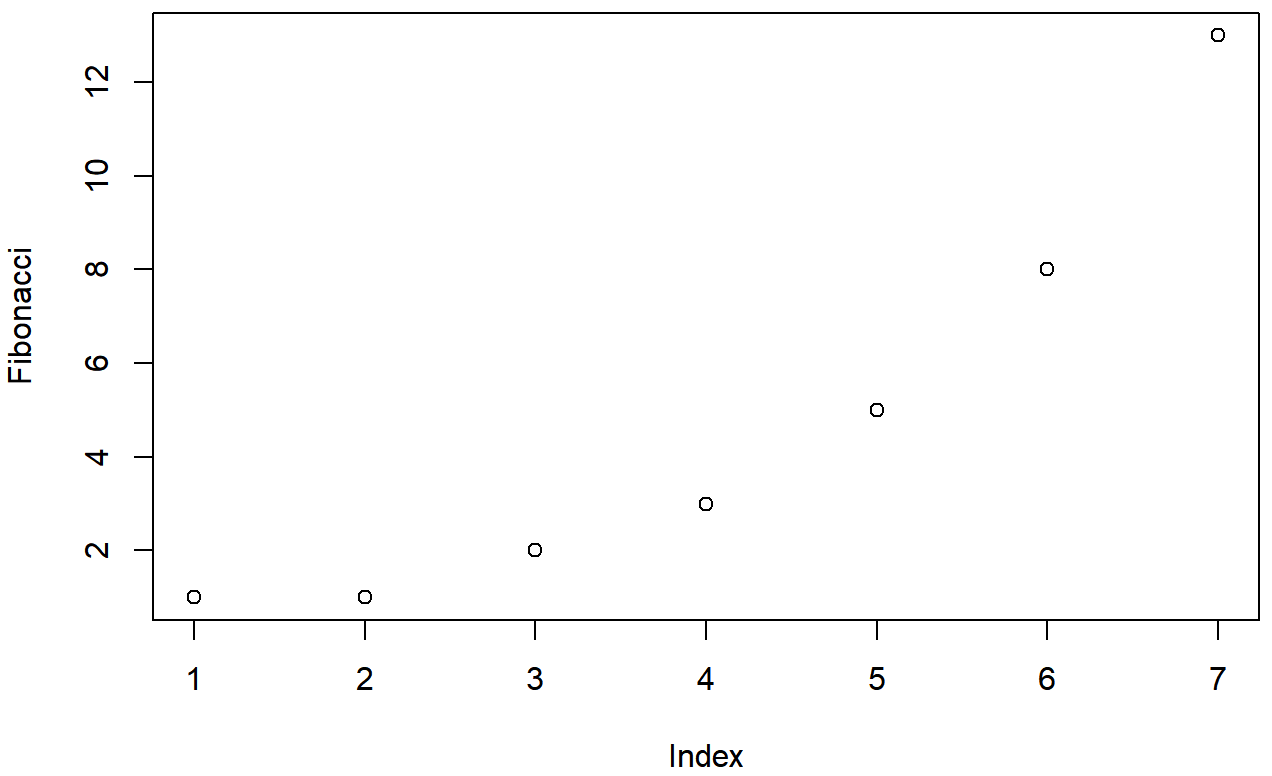
Como puede ver, lo que ha hecho R es trazar los valores almacenados en la variable Fibonacci en el eje vertical (eje y) y el índice correspondiente en el eje horizontal (eje x). Es decir, dado que el 4º elemento del vector tiene un valor de 3, obtenemos un punto trazado en la ubicación (4,3). Eso es bastante sencillo, y la imagen en la Figura 6.2 probablemente esté bastante cerca de lo que habrías tenido en mente cuando sugerí que trazáramos los datos de Fibonacci. Sin embargo, hay bastantes opciones de personalización disponibles para ti, así que probablemente deberíamos dedicar un poco de tiempo a ver algunas de esas opciones. Entonces, ten cuidado: esto termina siendo una sección bastante larga, porque hay tantas posibilidades abiertas para ti. Sin embargo, no dejes que te abrume... si bien todas las opciones discutidas aquí son útiles para conocer, puedes arreglártelas bien solo conociendo algunas de ellas. ¡La única razón por la que he incluido todas estas cosas al principio es que termina haciendo que el resto del capítulo sea mucho más legible!
digresión tediosa
Antes de entrar en cualquier discusión sobre la personalización de parcelas, necesitamos un poco más de antecedentes. Lo importante a tener en cuenta al usar la función plot (), es que es otro ejemplo de una función genérica (Sección 4.11, al igual que print () y summary (), y así su comportamiento cambia dependiendo de qué tipo de entrada le des. Sin embargo, la función plot () es algo más elegante que las otras dos, y su comportamiento depende de dos argumentos, x (la primera entrada, que se requiere) e y (que es opcional). Esto lo hace (a) extremadamente poderoso una vez que lo dominas, y (b) hilarantemente impredecible, cuando no estás seguro de lo que estás haciendo. En la medida de lo posible, voy a tratar de dejar claro qué tipo de entradas producen qué tipo de salidas. Por ahora, sin embargo, basta con señalar que solo estoy haciendo un trazado muy básico, y como consecuencia todo el trabajo lo está haciendo la función plot.default ().
¿Qué tipos de personalizaciones podrían interesarnos? Si observa la documentación de ayuda para el método de trazado predeterminado (es decir, ¿escriba? plot.default o help (“plot.default”)) verás una lista muy larga de argumentos que puedes especificar para personalizar tu parcela. Hablaré de varios de ellos en un momento, pero primero quiero señalar algo que puede parecer bastante loco. Cuando miras todas las diferentes opciones de las que habla el archivo de ayuda, notarás que algunas de las opciones a las que se refiere son argumentos “apropiados” para la función plot.default (), pero también pasa a mencionar un montón de cosas que parecen como se supone que son argumentos, pero no están listados en la sección “Uso” del archivo, y la documentación los llama parámetros gráficos en su lugar. Aun así, suele ser posible tratarlos como si fueran argumentos de la función plotting. Muy extraño. Para evitar que mis lectores intenten encontrar un ladrillo y buscar la dirección de mi casa, mejor explicaré lo que está pasando; o al menos dar la esencia básica detrás de esto.
¿Qué es exactamente un parámetro gráfico? Básicamente, la idea es que hay algunas características de una parcela que son bastante universales: por ejemplo, independientemente del tipo de gráfico que estés dibujando, probablemente necesites especificar qué color usar para la trama, ¿verdad? Entonces, ¿esperarías que haya algo así como un argumento col para cada función gráfica en R? Bueno, algo así como. Para evitar tener cientos de argumentos para cada función, lo que hace R es referirse a un montón de estos “parámetros gráficos” que son de propósito bastante general. Los parámetros gráficos se pueden cambiar directamente mediante el uso de la función par () de bajo nivel, que discuto brevemente en la Sección?? aunque no con mucho detalle. Si miras los archivos de ayuda para los parámetros gráficos (es decir, ¿escribe? par) verás que hay muchos de ellos. Afortunadamente, (a) los ajustes por defecto son generalmente bastante buenos así que puedes ignorar la mayoría de los parámetros, y (b) como verás a medida que avanzamos por este capítulo, muy raramente necesitas usar par () directamente, porque puedes “fingir” que los parámetros gráficos son solo argumentos adicionales a tu función de alto nivel (p. ej. plot.default ()). En resumen... sí, R sí tiene estos “parámetros gráficos” alocados que pueden resultar bastante confusos. Pero en la mayoría de los usos básicos de las funciones de trazado, puedes actuar como si solo fueran argumentos adicionales indocumentados a tu función.
Personalización del título y las etiquetas de los ejes
Una de las primeras cosas que te encontrarás queriendo hacer al personalizar tu parcela es etiquetarla mejor. Es posible que desee especificar etiquetas de eje más apropiadas, agregar un título o agregar un subtítulo. Los argumentos que debes especificar para que esto suceda son:
principal. Una cadena de caracteres que contiene el título.sub. Una cadena de caracteres que contiene el subtítulo.xlab. Una cadena de caracteres que contiene la etiqueta del eje x.ylab. Una cadena de caracteres que contiene la etiqueta del eje y.
Estos no son parámetros gráficos, son argumentos para la función de alto nivel. Sin embargo, debido a que todas las funciones de alto nivel se basan en la misma función de bajo nivel para hacer el dibujo 90, los nombres de estos argumentos son idénticos para casi todas las funciones de alto nivel con las que me he encontrado. Echemos un vistazo a lo que sucede cuando hacemos uso de todos estos argumentos. Aquí está el comando...
> plot( x = Fibonacci,
+ main = "You specify title using the 'main' argument",
+ sub = "The subtitle appears here! (Use the 'sub' argument for this)",
+ xlab = "The x-axis label is 'xlab'",
+ ylab = "The y-axis label is 'ylab'"
+ )El cuadro que este dibuja se muestra en la Figura 6.3.
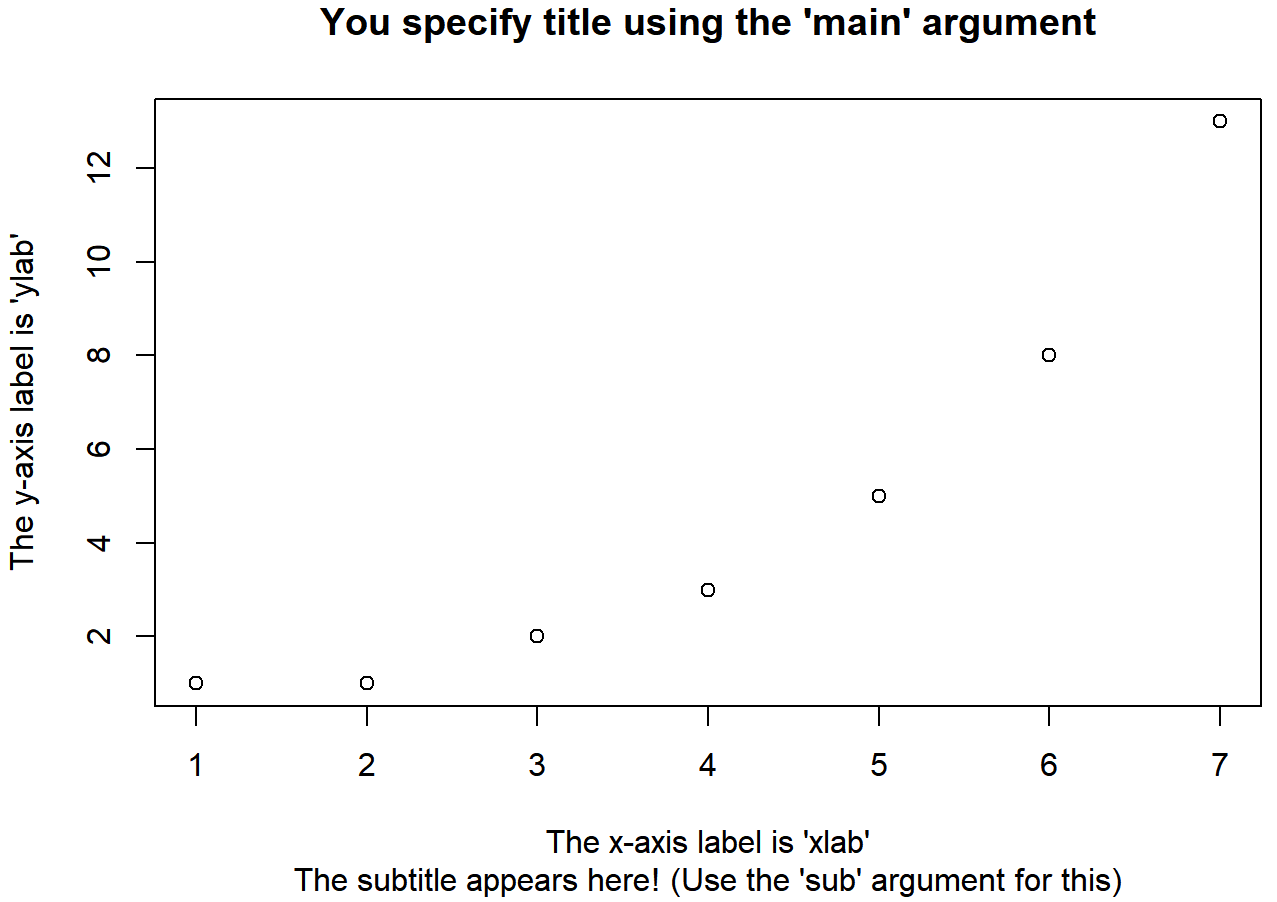
Es más o menos como cabría esperar. La trama en sí es idéntica a la que dibujamos en la Figura 6.2, excepto por el hecho de que hemos cambiado las etiquetas de los ejes, y agregado un título y un subtítulo. Aun así, hay un par de características interesantes a las que vale la pena llamar su atención. En primer lugar, observe que el subtítulo está dibujado debajo de la trama, lo que personalmente me parece molesto; como consecuencia casi nunca uso subtítulos. Puede que tengas una opinión diferente, claro, pero lo importante es que recuerdes a dónde va realmente el subtítulo. En segundo lugar, observe que R ha decidido usar texto en negrita y un tamaño de fuente más grande para el título. Esta es una de mis configuraciones predeterminadas más odiadas en los gráficos R, ya que siento que llama demasiado la atención sobre el título. Generalmente, aunque sí quiero que mi lector mire el título, encuentro que los valores predeterminados de R son un poco abrumadores, así que a menudo me gusta cambiar la configuración. Para ello, hay un montón de parámetros gráficos que puedes usar para personalizar el estilo de fuente:
- Estilos de fuente:
font.main,font.sub,font.lab,font.axis. Estos cuatro parámetros controlan el estilo de fuente utilizado para el título de la trama (font.main), el subtítulo (font.sub), las etiquetas del eje (font.lab: tenga en cuenta que no puede especificar estilos separados para el eje x y el eje y sin usar comandos de bajo nivel) y los números junto a la marca marcas en el eje (font.axis). Algo irritante, estos argumentos son números en lugar de nombres significativos: un valor de 1 corresponde a texto sin formato, 2 significa negrita, 3 significa cursiva y 4 significa negrita cursiva y 4 significa negrita cursiva. - Colores de fuente:
col.main,col.sub,col.lab,col.axis. Estos parámetros hacen más o menos lo que dice el nombre: cada uno especifica una col our en la que escribir cada uno de los diferentes bits de texto. Convenientemente, R tiene una gran cantidad de colores con nombre (typecolours ()para ver una lista de más de 650 nombres de color que R conoce), por lo que puede usar el nombre en inglés del color para seleccionarlo. 91 Así, el valor del parámetro aquí cadena como“red”,“gray25"o“springgreen4"(sí, R realmente reconoce cuatro tonos diferentes de “spring green”). - Tamaño de fuente:
cex.main,cex.sub,cex.lab,cex.axis. El tamaño de la fuente se maneja de una manera un poco curiosa en R. La parte “cex” aquí es la abreviatura de “c haracter ex pansion”, y es esencialmente un valor de aumento. Por defecto, todos estos se establecen en un valor de 1, a excepción del título de la fuente:cex.maintiene un aumento predeterminado de 1.2, razón por la cual la fuente del título es 20% más grande que las demás. - Familia tipográfica:
family. Este argumento especifica una familia de fuentes a usar: la forma más sencilla de usarla es configurarla en“sans”,“serif”o“mono”, correspondiente a una fuente san serif, una fuente serif o una fuente monoespaciada. Si quieres, puedes dar el nombre de una fuente específica, pero ten en cuenta que diferentes sistemas operativos usan diferentes fuentes, por lo que probablemente sea más seguro mantenerlo simple. Mejor aún, a menos que tenga algunas objeciones profundas a los valores predeterminados de R, simplemente ignore este parámetro por completo. Eso es lo que suelo hacer.
Para darte una idea de cómo puedes usar estos parámetros para personalizar tus títulos, se puede usar el siguiente comando para dibujar la Figura 6.4:
> plot( x = Fibonacci, # the data to plot
+ main = "The first 7 Fibonacci numbers", # the title
+ xlab = "Position in the sequence", # x-axis label
+ ylab = "The Fibonacci number", # y-axis label
+ font.main = 1, # plain text for title
+ cex.main = 1, # normal size for title
+ font.axis = 2, # bold text for numbering
+ col.lab = "gray50" # grey colour for labels
+ )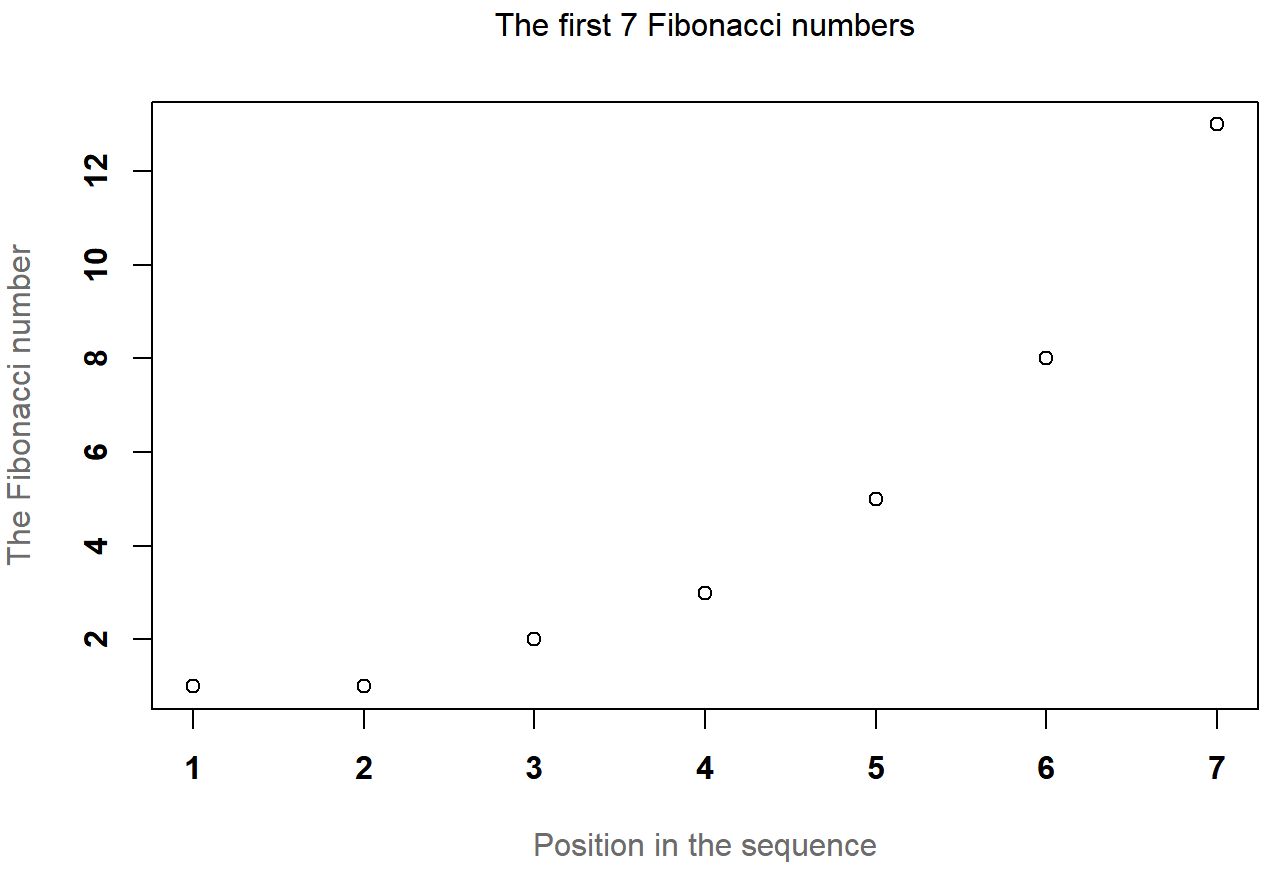
Aunque este comando es bastante largo, no es complicado: todo lo que hace es anular un montón de los valores de parámetros predeterminados. El único aspecto difícil de esto es que hay que recordar cómo se llama cada uno de estos parámetros, y cuáles son todos los diferentes valores. Y en la práctica nunca recuerdo: tengo que buscar la documentación de ayuda cada vez, o bien buscarla en este libro.
Cambiar el tipo de parcela
Agregar y personalizar los títulos asociados a la trama es una forma en la que puedes jugar con el aspecto de tu imagen. ¡Otra cosa que querrás hacer es personalizar la apariencia de la trama real! Para empezar, veamos las opciones más importantes que la función plot () (o, recordando que estamos tratando con una función genérica, en este caso la función plot.default (), ya que esa es la que hace todo el trabajo) proporciona para que la uses, que es el tipo argumento. El argumento type especifica el estilo visual de la trama. Los valores posibles para esto son:
type = “p”. Dibuja los p oints solamente.type = “l”. Dibuja una l ine a través de los puntos.type = “o”. Dibuja la línea o ver la parte superior de los puntos.tipo = “b”. Dibuja otros puntos y líneas, pero no exagere.type = “h”. Dibuja barras verticales tipo “h istograma”.type = “s”. Dibuja una s taircase, yendo horizontalmente y luego verticalmente.tipo = “S”. Dibuja una taircase S, yendo verticalmente y luego horizontalmente.type = “c”. Dibuja solo las c líneas de unión de la versión “b”.type = “n”. No dibuje nada. (Aparentemente esto es útil a veces?)
La forma más sencilla de ilustrar cómo se ve realmente cada uno de estos es simplemente dibujarlos. Para ello, la Figura 6.5 muestra los mismos datos de Fibonacci, dibujados utilizando seis tipos diferentes de parcelas. Como puedes ver, al alterar el argumento tipo puedes obtener una apariencia cualitativamente diferente a tu trama. En otras palabras, en lo que respecta a R, la única diferencia entre una gráfica de dispersión (como las que dibujamos en la Sección 5.7 y una gráfica de líneas es que dibujas una gráfica de dispersión estableciendo type = “p” y dibujas una gráfica de líneas estableciendo type = “l”. Sin embargo, eso no implica que debas pensar en ellos como empezar equivalentes entre sí. Como puede ver al observar la Figura 6.5, una gráfica lineal implica que existe alguna noción de continuidad de un punto a otro, mientras que una gráfica de dispersión no.
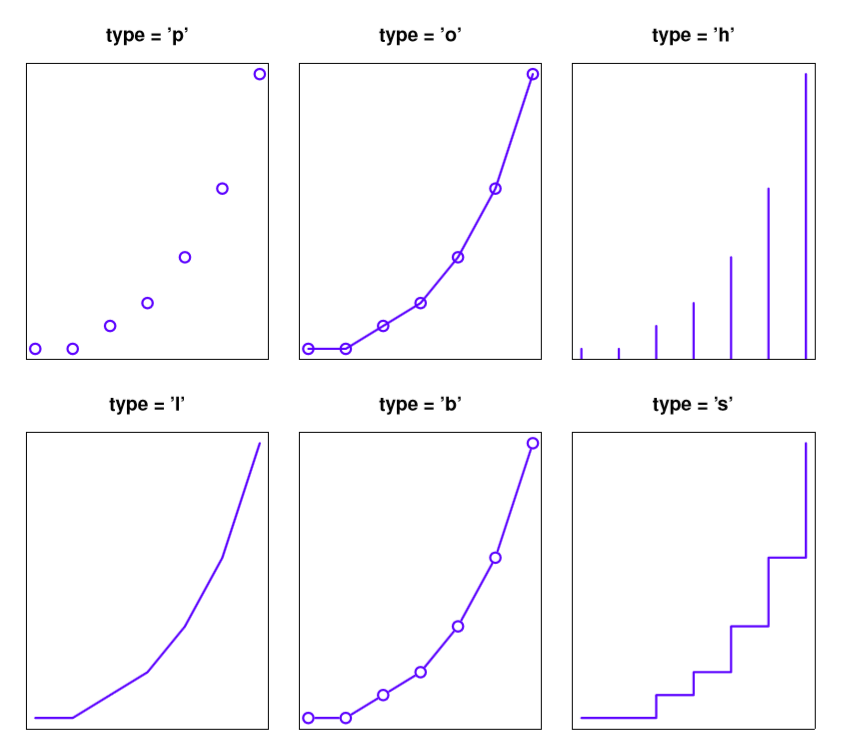
tipo de parcela.Cambio de otras características de la parcela

En Sección?? hablamos de un grupo de parámetros gráficos que están relacionados con el formateo de títulos, etiquetas de ejes etc. El segundo grupo de parámetros que quiero discutir son los relacionados con el formateo de la trama misma:
- Color de la parcela:
col. Como vimos con los parámetros anteriores relacionados con el color, la forma más sencilla de especificar este parámetro es usando una cadena de caracteres: por ejemplo,col = “azul”. Es un parámetro bastante sencillo de especificar: la única sutileza real es que cada función de alto nivel tiende a dibujar una “cosa” diferente a medida que es la salida, y así este parámetro es interpretado de manera un poco diferente por diferentes funciones. Sin embargo, para la funciónplot.default ()es bastante simple: ¡el argumentocolse refiere al color de los puntos y/o líneas que se dibujan! - Carácter utilizado para trazar puntos:
pch. El parámetro p lot ch aracter es un número, generalmente entre 1 y 25. Lo que hace es decirle a R qué símbolo usar para dibujar los puntos que traza. La forma más sencilla de ilustrar lo que hacen los diferentes valores es con una imagen. La Figura 6.6 a muestra los primeros 25 caracteres de trazado. El carácter de trazado predeterminado es un círculo hueco (es decir,pch = 1). - Tamaño de la parcela:
cex. Este parámetro describe un factor c haracter ex pansion (i.e., aumento) para los caracteres trazados. Por defectocex=1, pero si quieres símbolos más grandes en tu gráfica debes especificar un valor mayor. - Tipo de línea:
lty. El parámetro l ine ty pe describe el tipo de línea que dibuja R. Tiene siete valores que puedes especificar usando un número entre0y7, o usando una cadena de caracteres significativa:“blank”,“solid”,“dashed”,“punteado”,“dotdash”,“longdash”o“twodash”. Tenga en cuenta que la versión “en blanco” (valor 0) solo significa que R no dibuja las líneas en absoluto. Las otras seis versiones se muestran en la Figura 6.6 b. - Ancho de línea:
lwd. El último parámetro gráfico de esta categoría que quiero mencionar es el parámetro l ine w i d th, que es solo un número que especifica el ancho de la línea. El valor predeterminado es 1. No es sorprendente que los valores más grandes produzcan líneas más gruesas y los valores más pequeños producen líneas más delgadas. Intenta jugar con diferentes valores delwdpara ver qué pasa.
Para ilustrar lo que puede hacer alterando estos parámetros, intentemos el siguiente comando:
> plot( x = Fibonacci, # the data set
+ type = "b", # plot both points and lines
+ col = "blue", # change the plot colour to blue
+ pch = 19, # plotting character is a solid circle
+ cex = 5, # plot it at 5x the usual size
+ lty = 2, # change line type to dashed
+ lwd = 4 # change line width to 4x the usual
+ )La salida se muestra en la Figura 6.7.
plot( x = Fibonacci,
type = "b",
col = "blue",
pch = 19,
cex=5,
lty=2,
lwd=4)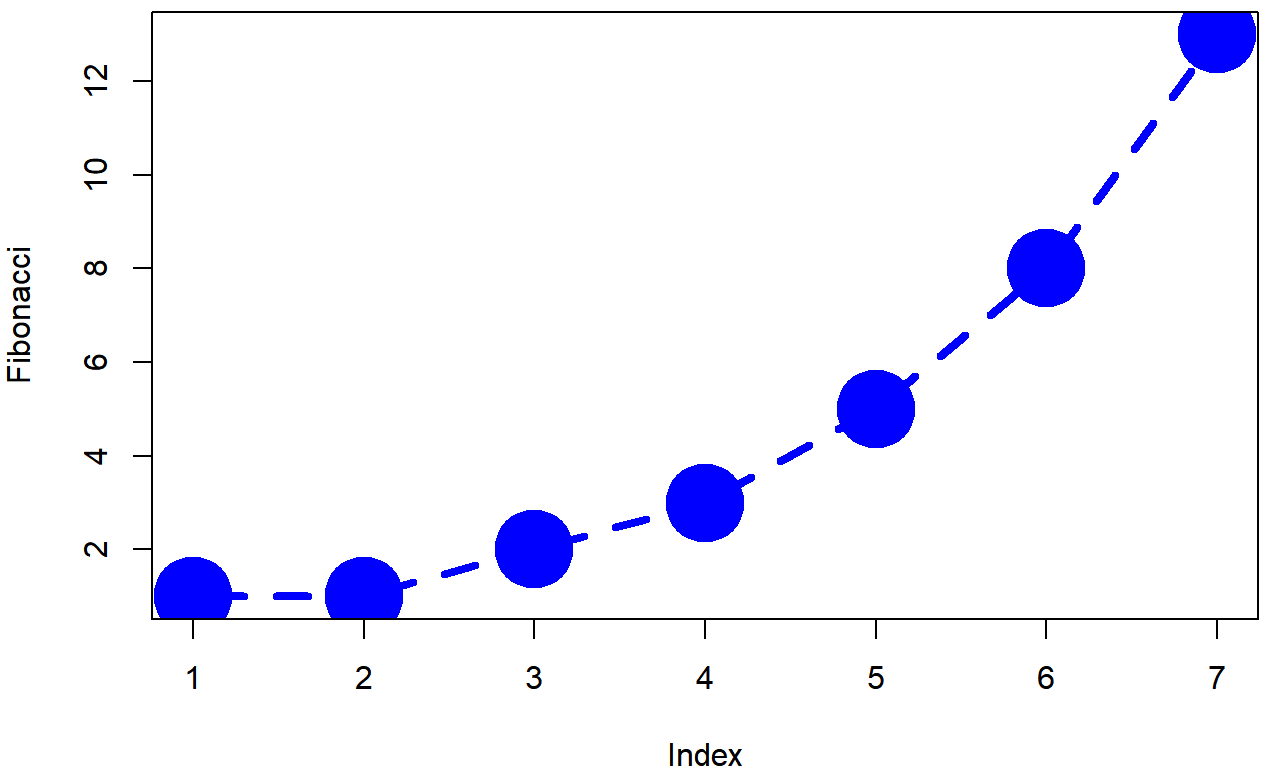
Cambiar la apariencia de los ejes
Hay varias otras posibilidades que vale la pena discutir. Ignorando los parámetros gráficos por el momento, hay algunos otros argumentos para la función plot.default () que quizás quieras usar. Como antes, muchos de estos son argumentos estándar que son utilizados por muchas funciones gráficas de alto nivel:
- Cambiando las escalas del eje:
xlim,ylim. Generalmente R hace un trabajo bastante bueno al averiguar dónde establecer los bordes de la trama. Sin embargo, puede anular sus elecciones estableciendo los argumentosxlimeylim. Por ejemplo, si decido que quiero que la escala vertical de la trama pase de 0 a 100, entonces estableceríaylim = c (0, 100). - Suprimir etiquetado:
ann. Este es un argumento de valor lógico que puedes usar si no quieres que R incluya ningún texto para un título, subtítulo o etiqueta de eje. Para ello, establezcaann = FALSE. Esto impedirá que R incluya cualquier texto que normalmente aparecería en esos lugares. Tenga en cuenta que esto anulará cualquiera de sus títulos manuales. Por ejemplo, si intentas agregar un título usando el argumentoprincipal, pero también especificasann = FALSO, no aparecerá ningún título. - Suprimir dibujo de ejes
: ejes. Nuevamente, este es un argumento lógico valorado. Supongamos que no quiere que R dibuje ningún eje en absoluto. Para suprimir los ejes, todo lo que tienes que hacer es agregarejes = FALSO. Esto eliminará los ejes y la numeración, pero no las etiquetas de los ejes (es decir, el textoxlabeylab). Tenga en cuenta que puede obtener un control de grano más fino sobre esto especificando los parámetros gráficosxaxtyyaxten su lugar (ver más abajo). - Incluya una caja de encuadre:
frame.plot. Supongamos que ha eliminado los ejes estableciendoejes = FALSO, pero aún así quiere tener un cuadro simple dibujado alrededor de la trama; es decir, solo quería deshacerse de la numeración y las marcas de verificación, pero quiere quedarse con la casilla. Para ello, establecesframe.plot = VERDADERO.
Tenga en cuenta que esta lista no es exhaustiva. Hay algunos otros argumentos para la función plot.default con los que puedes jugar si quieres, pero esos son los que probablemente quieras usar. Como siempre, sin embargo, si estas no son suficientes opciones para ti, también hay una serie de otros parámetros gráficos con los que quizás quieras jugar también. Ese es el foco de la siguiente sección. Mientras tanto, aquí hay un comando que hace uso de todas estas diferentes opciones:
> plot( x = Fibonacci, # the data
+ xlim = c(0, 15), # expand the x-scale
+ ylim = c(0, 15), # expand the y-scale
+ ann = FALSE, # delete all annotations
+ axes = FALSE, # delete the axes
+ frame.plot = TRUE # but include a framing box
+ )La salida se muestra en la Figura 6.8, y es más o menos exactamente como cabría esperar. Las escalas de ejes tanto en las dimensiones horizontal como vertical se han expandido, los ejes se han suprimido al igual que las anotaciones, pero he guardado una caja alrededor de la trama.
plot( x = Fibonacci,
xlim = c(0, 15),
ylim = c(0, 15),
ann = FALSE,
axes = FALSE,
frame.plot = TRUE)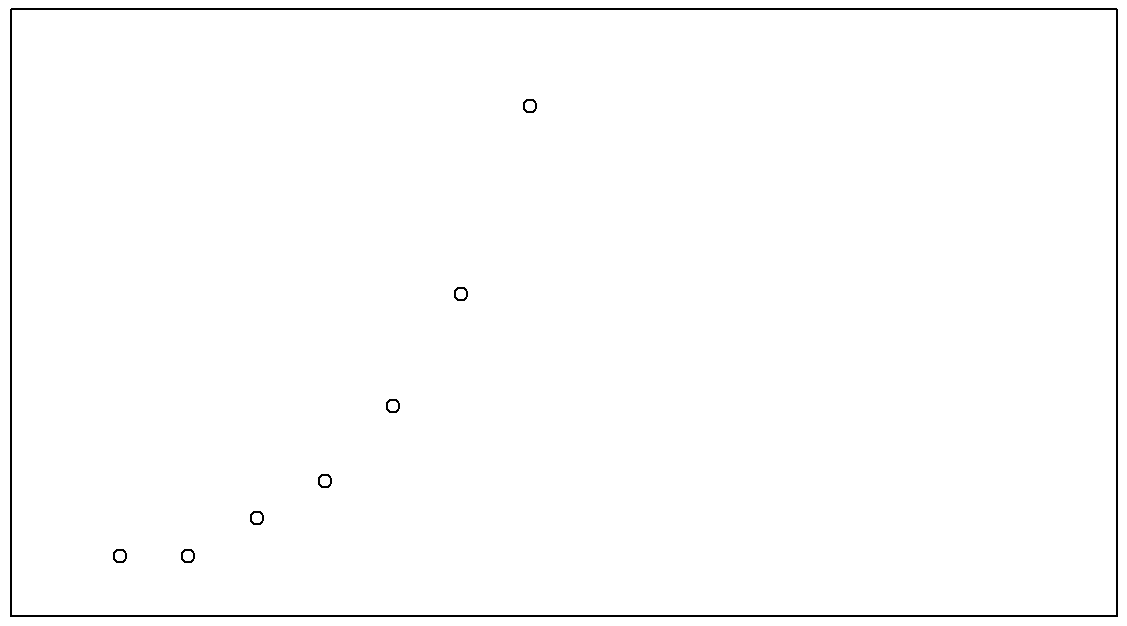
Antes de continuar, debo señalar que existen varios parámetros gráficos relacionados con los ejes, la caja y el aspecto general de la parcela que permiten un control de grano más fino sobre la apariencia de los ejes y las anotaciones.
- Suprimiendo los ejes individualmente:
xaxt,yaxt. Estos parámetros gráficos son básicamente solo versiones más elegantes del argumento deejesque discutimos anteriormente. Si quieres evitar que R dibuje el eje vertical pero quieres que mantenga el eje horizontal, estableceyaxt = “n”. ¡Confío en que puedas averiguar cómo mantener el eje vertical y suprimir el horizontal! - Tipo de caja:
bty. De la misma manera quexaxt,yaxtson solo versiones elegantes deejes, el parámetro b ox ty pe es realmente solo una versión más elegante del argumentoframe.plot, lo que le permite especificar exactamente cuál de los cuatro bordes desea mantener. La forma en que especificamos este parámetro es un poco estúpida, en mi opinión: los valores posibles son“o”(el predeterminado),“l”,“7",“c”,“u”, o“]”, cada uno de los cuales dibujará solo aquellos bordes que sugiere el carácter correspondiente. Es decir, la letra“c”tiene una parte superior, una inferior y una izquierda, pero está en blanco en el lado derecho, mientras que“7"tiene una parte superior y una derecha, pero está en blanco a la izquierda y la inferior. Alternativamente, un valor de“n”significa que no se dibujará ninguna caja. - Orientación de las etiquetas del eje
las. Supongo que el nombre de este parámetro es un acrónimo de la bel s tyle o algo a lo largo de esas líneas; pero lo que realmente hace es gobernar la orientación del texto utilizado para etiquetar las marcas de verificación individuales (es decir, la numeración, no el ejexlabeylabetiquetas). Hay cuatro valores posibles paralas: Un valor de 0 significa que las etiquetas de ambos ejes se imprimen paralelas al eje mismo (el valor predeterminado). Un valor de 1 significa que el texto es siempre horizontal. Un valor de 2 significa que el texto de etiquetado se imprime en ángulo recto con el eje. Por último, un valor de 3 significa que el texto siempre es vertical.
Nuevamente, estas no son las únicas posibilidades. Hay algunos otros parámetros gráficos que no he mencionado que podrías usar para personalizar la apariencia de los ejes, 92 pero eso probablemente sea suficiente (o más que suficiente) por ahora. Para dar una idea de cómo podrías usar estos parámetros, probemos el siguiente comando:
> plot( x = Fibonacci, # the data
+ xaxt = "n", # don't draw the x-axis
+ bty = "]", # keep bottom, right and top of box only
+ las = 1 # rotate the text
+ )La salida se muestra en la Figura 6.9. Como puedes ver, esta no es una trama muy útil en absoluto. Sin embargo, sí ilustra los parámetros gráficos de los que estamos hablando, así que supongo que sirve a su propósito.
plot( x = Fibonacci,
xaxt = "n",
bty = "]",
las = 1 )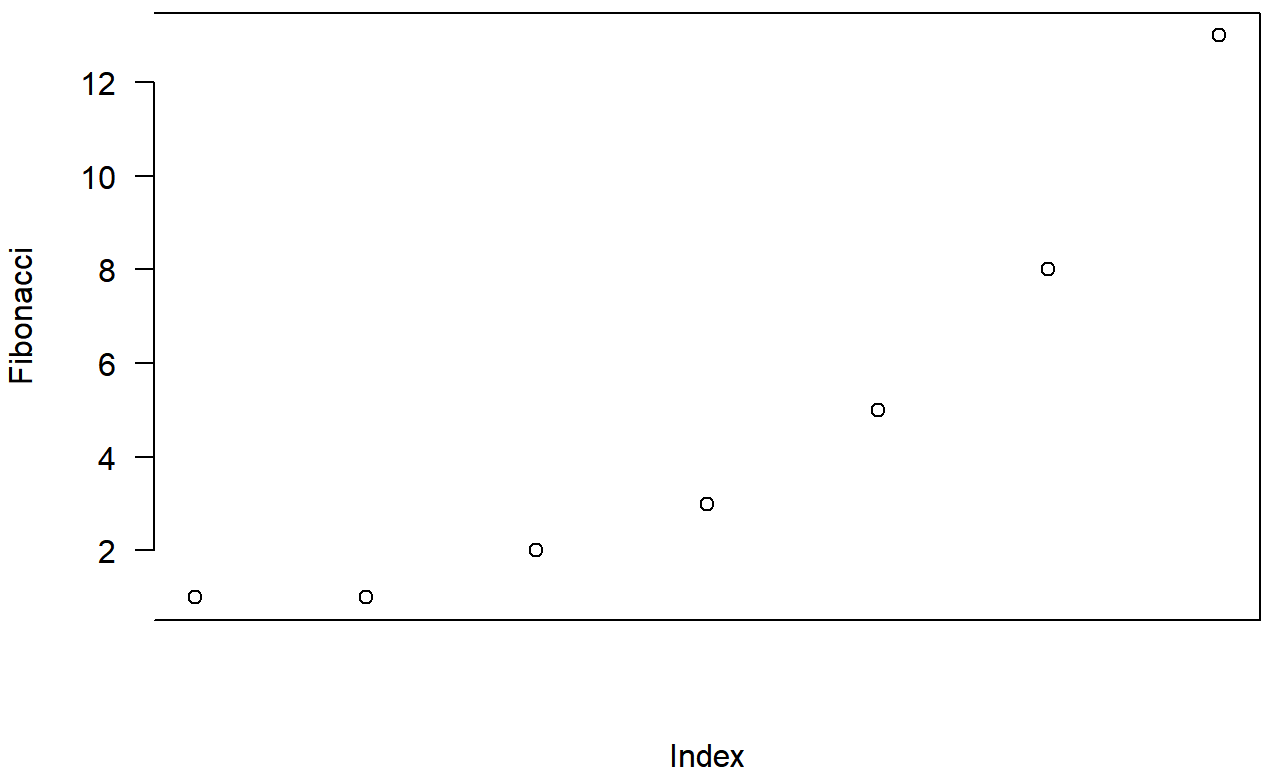
No entre en pánico
En este punto, probablemente muchos lectores estarán pensando algo en la línea de, “si hay tanto detalle solo por dibujar una trama simple, ¿qué tan horrible se va a poner cuando empecemos a mirar cosas más complicadas?” Quizás, contrariamente a mis anteriores súplicas de misericordia, has encontrado un ladrillo para lanzar y ahora mismo estás hojeando una guía telefónica de Adelaida tratando de encontrar mi dirección. Bueno, ¡no temas! Y por favor, baje el ladrillo. En muchos sentidos, hemos pasado por la parte más difícil: ya hemos cubierto la gran mayoría de las personalizaciones de la trama que quizás quieras hacer. Como verás, cada uno de los otros comandos de trazado de alto nivel de los que hablaremos solo tendrá un número pequeño de opciones adicionales. Mejor aún, a pesar de que te he hablado de mil millones de formas diferentes de ajustar tu trama, normalmente no las necesitas. Entonces, en la práctica, ahora que lo has leído una vez para obtener la esencia, la mayor parte del contenido de esta sección son cosas que puedes olvidar con seguridad: solo recuerda volver a esta sección más adelante cuando quieras modificar tu trama.


