15.1: ¿Qué es un modelo de regresión lineal?
- Page ID
- 151893
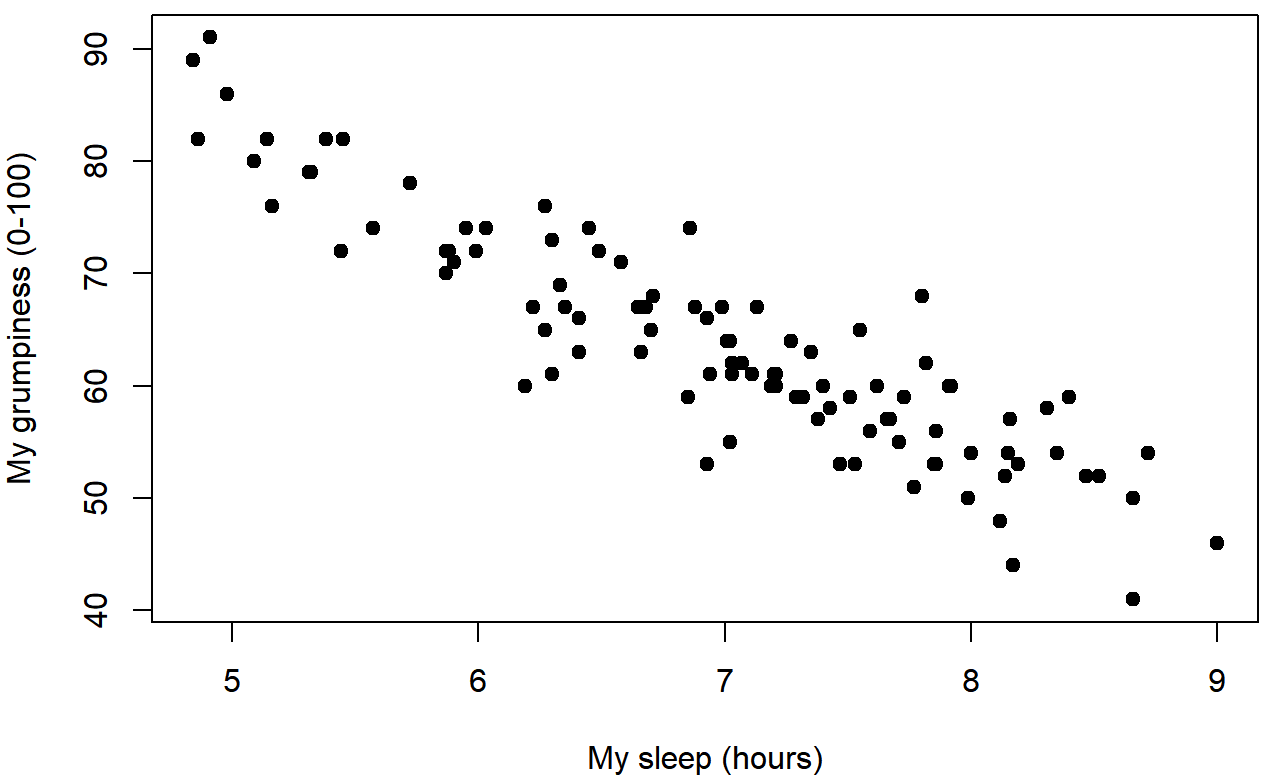
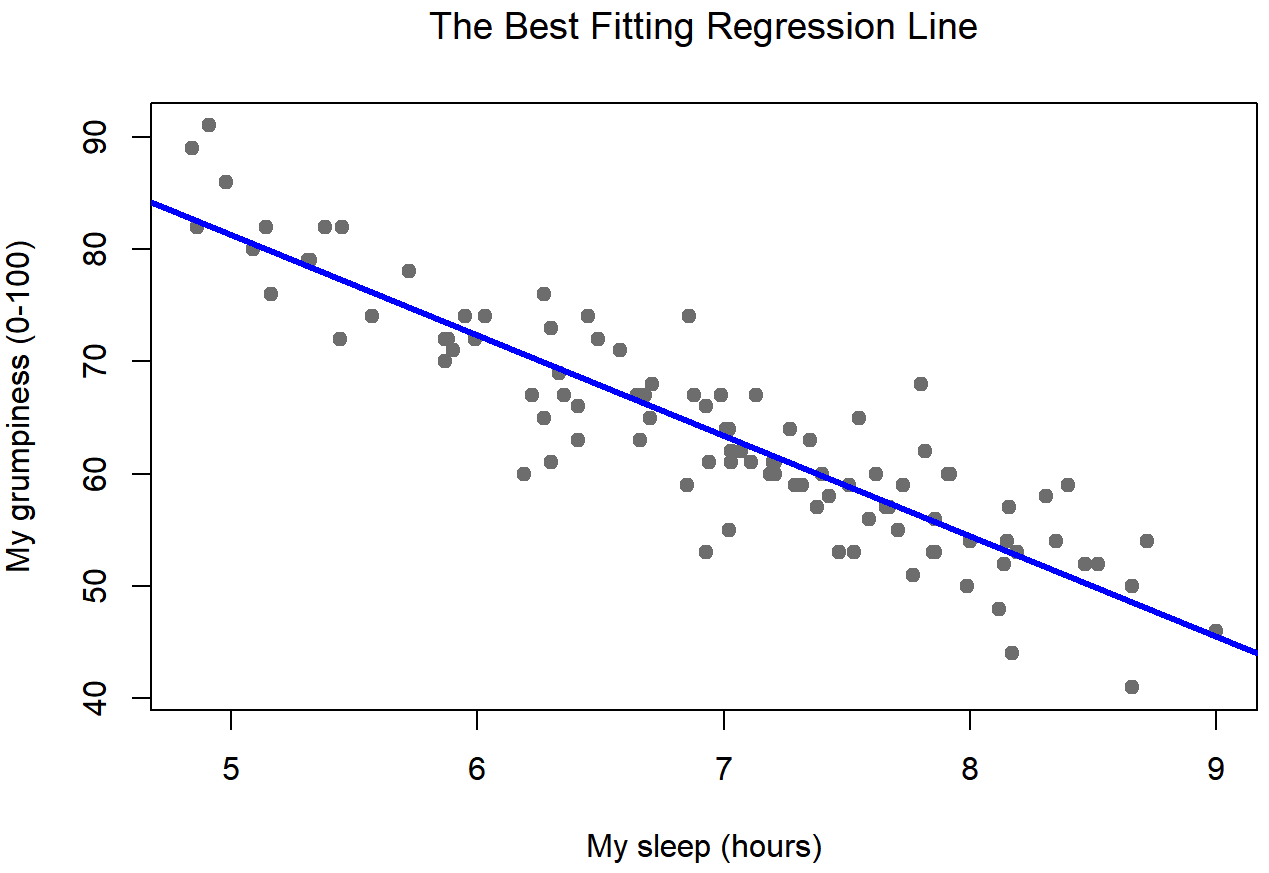
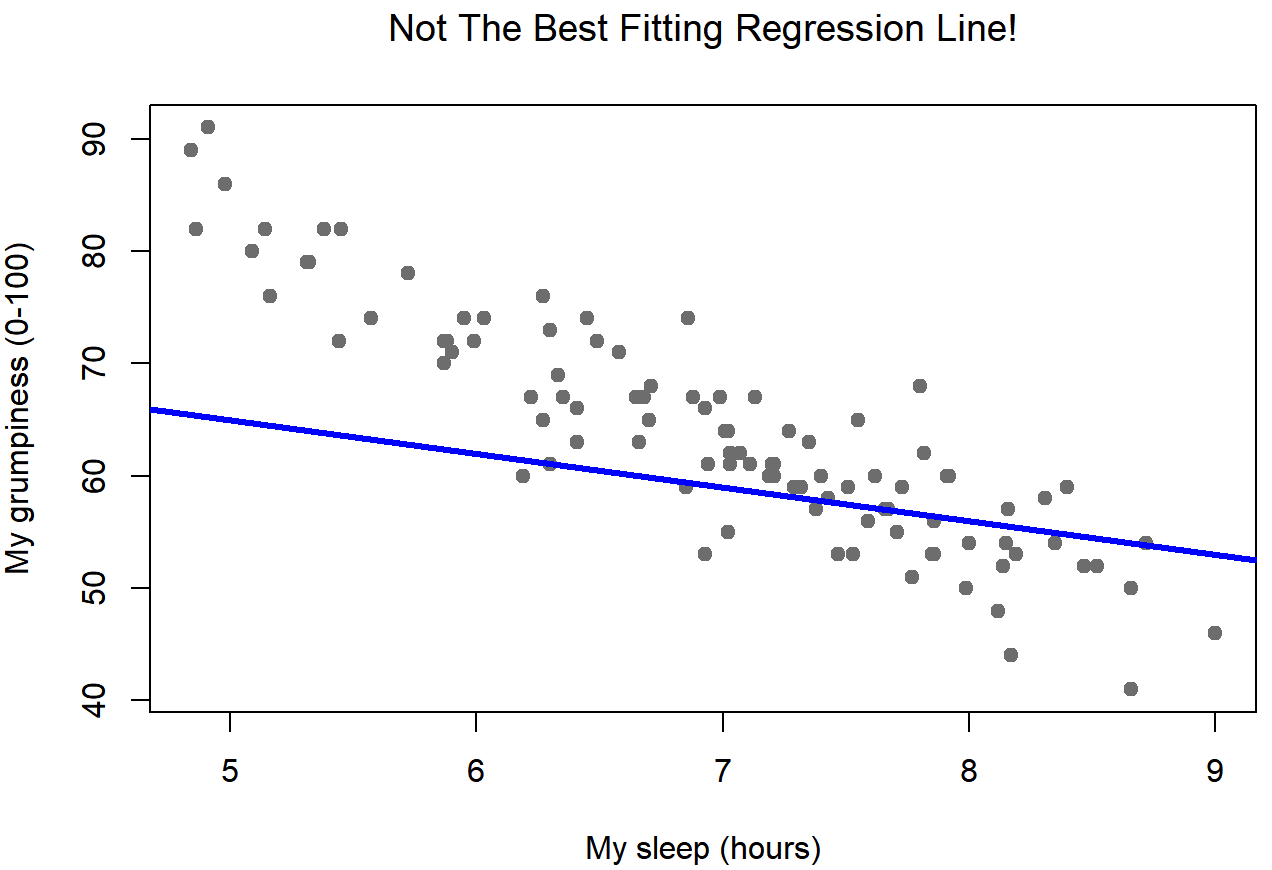
Dado que las ideas básicas en regresión están estrechamente ligadas a la correlación, volveremos al archivo Parenthood.rdata que estábamos usando para ilustrar cómo funcionan las correlaciones. Recordemos que, en este conjunto de datos, estábamos tratando de averiguar por qué Dan está tan gruñón todo el tiempo, y nuestra hipótesis de trabajo era que no estoy durmiendo lo suficiente. Dibujamos algunas tramas de dispersión para ayudarnos a examinar la relación entre la cantidad de sueño que tengo y mi maldad al día siguiente. La gráfica de dispersión real que dibujamos es la que se muestra en la Figura 15.1, y como vimos anteriormente esta corresponde a una correlación de r=−.90, pero lo que nos encontramos imaginando secretamente es algo que mira más cerca de la Figura 15.2. Es decir, trazamos mentalmente una línea recta a través de la mitad de los datos. En estadística, esta línea que estamos dibujando se llama línea de regresión. Observe que —como no somos idiotas— la línea de regresión pasa por la mitad de los datos. No nos encontramos imaginando nada como la trama bastante tonta que se muestra en la Figura 15.3.
Esto no es muy sorprendente: la línea que he dibujado en la Figura 15.3 no “encaja” muy bien con los datos, por lo que no tiene mucho sentido proponerlo como una forma de resumir los datos, ¿verdad? Esta es una observación muy sencilla de hacer, pero resulta ser muy poderosa cuando empezamos a tratar de envolverlo solo un poquito de matemáticas. Para ello, comencemos con un repaso de algunas matemáticas de secundaria. La fórmula para una línea recta suele escribirse así:
y=mx+c
O, al menos, eso fue lo que era cuando fui a la preparatoria hace todos esos años. Las dos variables son x e y, y tenemos dos coeficientes, m y c. El coeficiente m representa la pendiente de la línea, y el coeficiente c representa la intercepción y de la línea. Cavando más atrás en nuestros decayentes recuerdos de la secundaria (lo siento, para algunos de nosotros la secundaria fue hace mucho tiempo), recordamos que la intercepción se interpreta como “el valor de y que obtienes cuando x=0”. De manera similar, una pendiente de m significa que si aumenta el valor x en 1 unidad, entonces el valor y sube en m unidades; una pendiente negativa significa que el valor y bajaría en lugar de subir. Ah, sí, ya me está volviendo todo.
Ahora que lo hemos recordado, no debería sorprendernos descubrir que usamos exactamente la misma fórmula para describir una línea de regresión. Si Y es la variable de resultado (la DV) y X es la variable predictora (la IV), entonces la fórmula que describe nuestra regresión se escribe así:
\(\ \hat{Y_i} = b_1X_i + b_0\)
Hm. Parece la misma fórmula, pero hay algunos pedacitos extra con volante en esta versión. Asegurémonos de entenderlos. En primer lugar, observe que he escrito X i e Y i en lugar de simplemente X e Y. Esto se debe a que queremos recordar que estamos tratando con datos reales. En esta ecuación, X i es el valor de la variable predictora para la i-ésima observación (es decir, el número de horas de sueño que obtuve el día i de mi pequeño estudio), e Y i es el valor correspondiente de la variable de resultado (es decir, mi maldad en ese día). Y aunque no lo he dicho explícitamente en la ecuación, lo que estamos asumiendo es que esta fórmula funciona para todas las observaciones en el conjunto de datos (es decir, para todos i). En segundo lugar, fíjate que escribí\(\ \hat{Y_i}\) y no Yi. Esto se debe a que queremos hacer la distinción entre los datos reales Y i, y la estimación\(\ \hat{Y_i}\) (es decir, la predicción que está haciendo nuestra línea de regresión). En tercer lugar, cambié las letras utilizadas para describir los coeficientes de m y c a b 1 y b 0. Esa es la forma en que a los estadísticos les gusta referirse a los coeficientes en un modelo de regresión. No tengo idea de por qué eligieron b, pero eso es lo que hicieron. En cualquier caso b 0 siempre se refiere al término de intercepción, y b1 se refiere a la pendiente.
Excelente, excelente. A continuación, no puedo evitar notar que —independientemente de que estemos hablando de la línea de regresión buena o de la mala— los datos no caen perfectamente en la línea. O, para decirlo de otra manera, los datos Yi no son idénticos a las predicciones del modelo de regresión\(\ \hat{Y_i}\). Dado que a los estadísticos les encanta adjuntar letras, nombres y números a todo, vamos a referirnos a la diferencia entre la predicción del modelo y ese punto de datos real como residual, y nos referiremos a él como i. 214 Escrito usando matemáticas, los residuos se definen como:
\(\ \epsilon_i = Y_i - \hat{Y_i}\)
lo que a su vez significa que podemos anotar el modelo de regresión lineal completo como:
\(\ Y_i = b_1X_i + b_0 + \epsilon_i\)


