15.2: Estimación de un modelo de regresión lineal

Figura 15.4: Una representación de los residuos asociados con la línea de regresión de mejor ajuste

Figura 15.5: Los residuos asociados a una mala línea de regresión

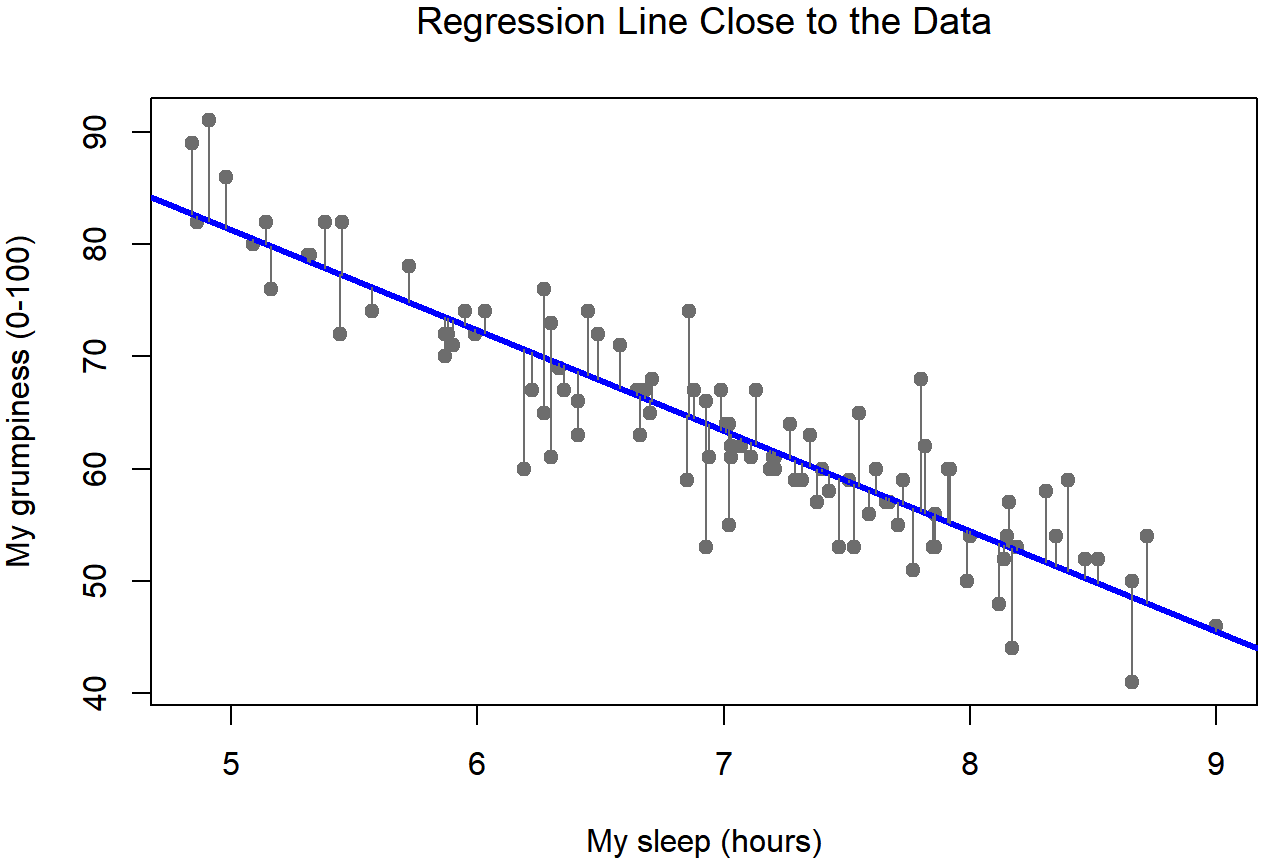
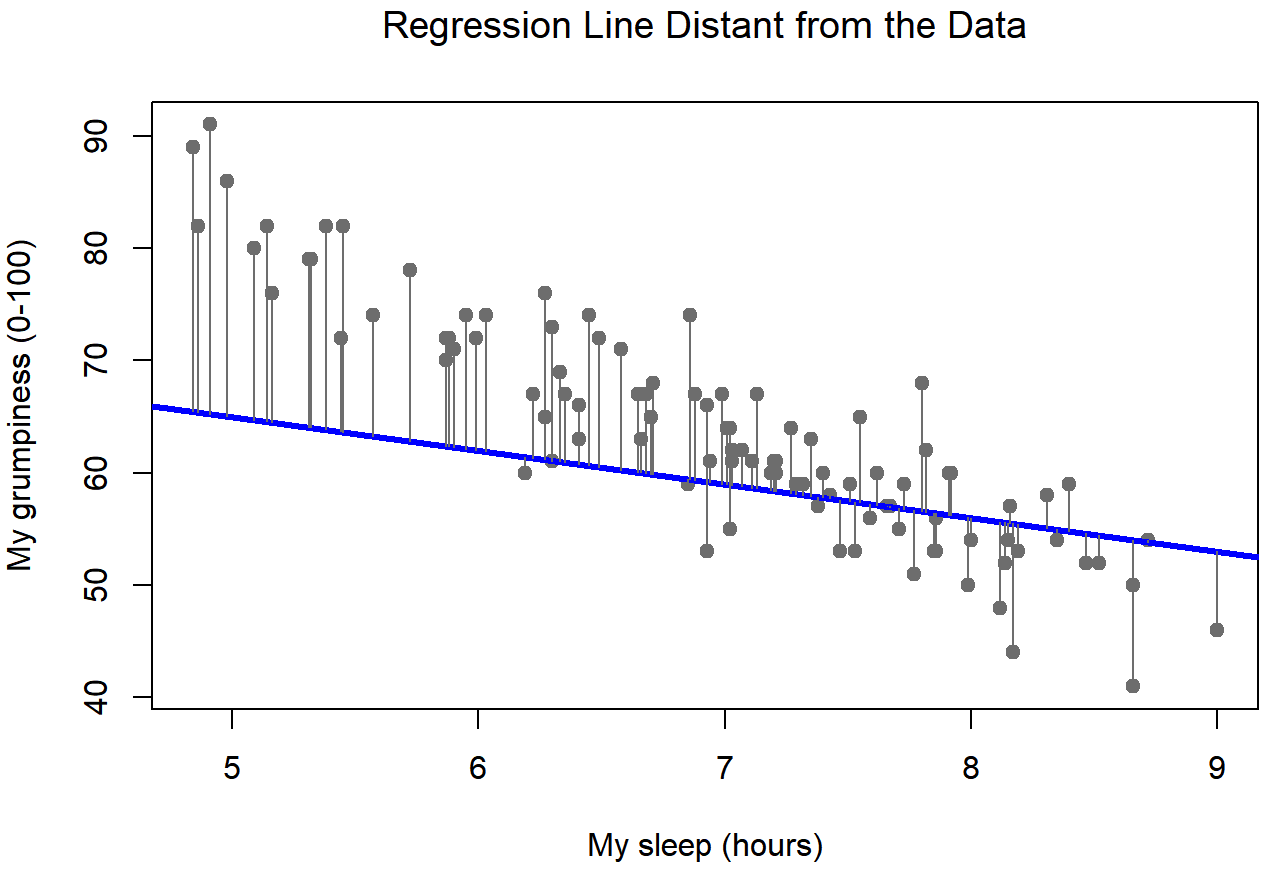
Bien, ahora vamos a volver a dibujar nuestras imágenes, pero esta vez voy a añadir algunas líneas para mostrar el tamaño del residuo para todas las observaciones. Cuando la línea de regresión es buena, nuestros residuales (las longitudes de las líneas negras continuas) todos se ven bastante pequeños, como se muestra en la Figura 15.4, pero cuando la línea de regresión es mala, los residuales son mucho más grandes, como se puede ver al mirar la Figura 15.5. Hm. Tal vez lo que “queremos” en un modelo de regresión son pequeños residuos. Sí, eso sí parece tener sentido. De hecho, creo que llegaré tan lejos como para decir que la línea de regresión “mejor ajustada” es la que tiene los residuos más pequeños. O, mejor aún, ya que parece que a los estadísticos les gusta tomar cuadrados de todo por qué no decir eso...

Los coeficientes de regresión estimados,\(\ \hat{b_0}\) y\(\hat{b_1}\) son aquellos que minimizan la suma de los residuos cuadrados, los cuales podríamos escribir como\(\sum_{i}\left(Y_{i}-\hat{Y}_{i}\right)^{2}\) o como\(\sum_{i} \epsilon_{i}^{2}\).

Sí, sí eso suena aún mejor. Y como lo he sangrado así, probablemente signifique que esta es la respuesta correcta. Y como esta es la respuesta correcta, probablemente valga la pena tomar nota del hecho de que nuestros coeficientes de regresión son estimaciones (¡estamos tratando de adivinar los parámetros que describen a una población!) , por lo que he añadido los sombreritos, para que obtengamos\(\ \hat{b_0}\) y\(\ \hat{b_1}\) en lugar de b0 y b1. Por último, también debo señalar que —dado que en realidad hay más de una manera de estimar un modelo de regresión— el nombre más técnico para este proceso de estimación es la regresión de mínimos cuadrados ordinarios (OLS).

En este punto, ahora tenemos una definición concreta de lo que cuenta como nuestra “mejor” elección de coeficientes de regresión,\(\ \hat{b_0}\) y\(\ \hat{b_1}\). La pregunta natural a hacer a continuación es, si nuestros coeficientes de regresión óptimos son los que minimizan la suma de los residuos cuadrados, ¿cómo encontramos estos maravillosos números? La respuesta real a esta pregunta es complicada, y no te ayuda a entender la lógica de la regresión. ²¹⁵ Como resultado, esta vez voy a dejarte descolgado. En lugar de mostrarte cómo hacerlo primero de la manera larga y tediosa, y luego “revelar” el maravilloso atajo que R te proporciona, cortemos directo al grano... y utilicemos la función lm () (abreviatura de “modelo lineal”) para hacer todo el trabajo pesado.

Uso de la función lm ()

La función lm () es bastante complicada: si escribes? lm, los archivos de ayuda revelarán que hay muchos argumentos que puedes especificar, y la mayoría de ellos no tendrán mucho sentido para ti. En esta etapa sin embargo, realmente solo hay dos de ellos que te importan, y como resulta que los has visto antes:

• fórmula. Una fórmula que especifica el modelo de regresión. Para los modelos de regresión lineal simple de los que hemos hablado hasta ahora, en los que se tiene una sola variable predictora así como un término de intercepción, esta fórmula es de la forma result ~ predictor. No obstante, se permiten fórmulas más complicadas, y las discutiremos más adelante.
• datos. El marco de datos que contiene las variables.

Como vimos con aov () en el Capítulo 14, la salida de la función lm () es un objeto bastante complicado, con bastante información técnica enterrada bajo el capó. Debido a que esta información técnica es utilizada por otras funciones, generalmente es una buena idea crear una variable que almacene los resultados de su regresión. Con esto en mente, para ejecutar mi regresión lineal, el comando que quiero usar es este:

regression.1 <- lm( formula = dan.grump ~ dan.sleep,  
                    data = parenthood )  

Tenga en cuenta que usé dan.grump ~ dan.sleep como fórmula: en el modelo que estoy tratando de estimar, dan.grump es la variable de resultado, y dan.sleep es la variable predictora. Siempre es una buena idea recordar cuál es cuál! De todos modos, lo que esto hace es crear un “objeto lm” (es decir, una variable cuya clase es “lm”) llamada regresion.1. Echemos un vistazo a lo que sucede cuando lo imprimimos ():

print( regression.1 )

## 
## Call:
## lm(formula = dan.grump ~ dan.sleep, data = parenthood)
## 
## Coefficients:
## (Intercept)    dan.sleep  
##     125.956       -8.937

Esto parece prometedor. Aquí hay dos piezas separadas de información. En primer lugar, R nos está recordando cortésmente cuál era el comando que usamos para especificar el modelo en primer lugar, lo que puede ser útil. Más importante desde nuestra perspectiva, sin embargo, es la segunda parte, en la que R nos da la intercepción\(\ \hat{b_0}\) =125.96 y la pendiente\(\ \hat{b_1}\) =−8.94. En otras palabras, la línea de regresión de mejor ajuste que representé en la Figura 15.2 tiene esta fórmula:

\(\ \hat{Y_i} = -8.94 \ X_i + 125.96\)

Interpretación del modelo estimado

Lo más importante para poder entender es cómo interpretar estos coeficientes. Empecemos con\(\ \hat{b_1}\), la pendiente. Si recordamos la definición de la pendiente, un coeficiente de regresión de\(\ \hat{b_1}\) =−8.94 significa que si _{aumento X i} en 1, entonces estoy disminuyendo Y _i en 8.94. Es decir, cada hora adicional de sueño que gane mejorará mi estado de ánimo, reduciendo mi maldad en 8.94 puntos de gruñidos. ¿Qué pasa con la interceptación? Bueno, ya que\(\ \hat{b_0}\) corresponde a “el valor esperado de Y _i cuando Xi es igual a 0”, es bastante sencillo. Implica que si consigo cero horas de sueño (X _i =0) entonces mi maldad se irá fuera de la escala, a un valor demente de (Y _i =125.96). Lo mejor es que se evite, creo.