4.3: Puntuaciones Z y el Área bajo la Curva
- Page ID
- 150971
\(Z\)-puntuaciones y la distribución normal estándar van de la mano. Un\(z\) -score le dirá exactamente dónde en la distribución normal estándar se encuentra un valor, y cualquier distribución normal se puede convertir en una distribución normal estándar convirtiendo todas las puntuaciones de la distribución en\(z\) -scores, un proceso conocido como estandarización.
Vimos en el capítulo anterior que las desviaciones estándar se pueden utilizar para dividir la distribución normal: 68% de la distribución cae dentro de 1 desviación estándar de la media, 95% dentro de (aproximadamente) 2 desviaciones estándar y 99.7% dentro de 3 desviaciones estándar. Debido a que las\(z\) puntuaciones -están en unidades de desviaciones estándar, esto significa que el 68% de las puntuaciones caen entre\(z\) = -1.0 y\(z\) = 1.0 y así sucesivamente. A esto le llamamos 68% (o cualquier porcentaje que tengamos basado en nuestras\(z\) puntuaciones) la proporción del área bajo la curva. Cualquier área bajo la curva está delimitada por (definida por, delineada por, etc.) por una sola\(z\) -score o par de\(z\) -scores.
Una propiedad importante a señalar aquí es que, en virtud de que el área total bajo la curva de una distribución siempre es igual a 1.0 (ver sección sobre Distribuciones normales al inicio de este capítulo), estas áreas bajo la curva pueden sumarse o restarse de 1 para encontrar la proporción en otras áreas. Por ejemplo, sabemos que el área entre\(z\) = -1.0 y\(z\) = 1.0 (es decir, dentro de una desviación estándar de la media) contiene 68% del área bajo la curva, que se puede representar en forma decimal a 0.6800 (para cambiar un porcentaje a un decimal, simplemente mueva el punto decimal 2 lugares hacia la izquierda ). Debido a que el área total bajo la curva es igual a 1.0, eso significa que la proporción del área exterior\(z\) = -1.0 y\(z\) = 1.0 es igual a 1.0 — 0.6800 = 0.3200 o 32% (ver Figura\(\PageIndex{1}\) a continuación). A esta zona se le llama el área en las colas de la distribución. Debido a que esta área se divide entre dos colas y debido a que la distribución normal es simétrica, cada cola tiene exactamente la mitad, o 16%, del área bajo la curva.
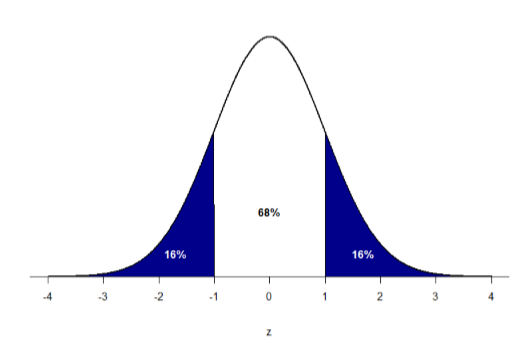
Tendremos mucho más que decir sobre este concepto en los próximos capítulos. Resulta que esta es una idea bastante poderosa que nos permite hacer declaraciones sobre cuán probable es un resultado y qué significa eso para las preguntas de investigación que nos gustaría responder y las hipótesis que nos gustaría probar. Pero primero, necesitamos hacer una breve incursión en algunas ideas sobre la probabilidad.


