11.1: Observar e interpretar la variabilidad
- Page ID
- 150917
Hemos visto una y otra vez que los puntajes, ya sean datos individuales o medios grupales, diferirán naturalmente. A veces esto se debe a la casualidad aleatoria, y otras veces se debe a diferencias reales. Nuestro trabajo como científicos, investigadores y analistas de datos es determinar si las diferencias observadas son sistemáticas y significativas (a través de una prueba de hipótesis) y, en caso afirmativo, qué está causando esas diferencias. A través de esto, queda claro que, aunque generalmente nos interesa la puntuación media o promedio, es la variabilidad en las puntuaciones lo que es clave.
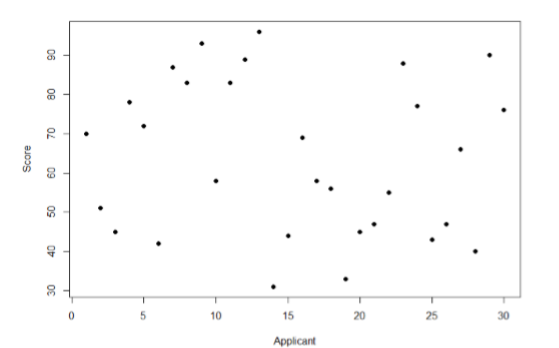
Eche un vistazo a Figure\(\PageIndex{1}\), que muestra los puntajes de muchas personas en una prueba de habilidad utilizada como parte de una solicitud de empleo. El\(x\) eje -tiene a cada persona individual, sin ningún orden en particular, y el\(y\) eje contiene la puntuación que cada persona recibió en la prueba. Como podemos ver, los solicitantes de empleo difirieron bastante en su desempeño, y entender por qué ese es el caso sería información sumamente útil. Sin embargo, no hay patrón interpretable en los datos, sobre todo porque solo tenemos información sobre la prueba, no sobre ninguna otra variable (recuerde que el eje x aquí solo muestra personas individuales y no está ordenado ni interpretable).
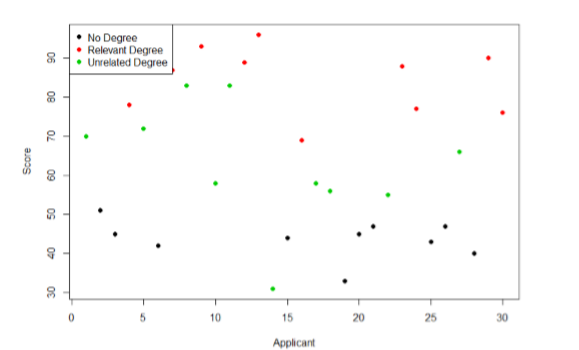
Nuestro objetivo es explicar esta variabilidad que estamos viendo en el conjunto de datos. Supongamos que como parte del procedimiento de solicitud de empleo también recopilamos datos sobre el grado más alto que obtuvo cada aspirante. Con conocimiento de lo que requiere el puesto, podríamos clasificar a nuestros aspirantes en tres grupos: aquellos aspirantes que tengan un título universitario relacionado con el puesto, aquellos aspirantes que tengan un título universitario que no esté relacionado con el puesto, y aquellos aspirantes que no obtuvieron un título universitario. Esta es una forma común de ordenar a los solicitantes de empleo, y podemos usar ANOVA para probar si estos grupos son realmente diferentes. La figura\(\PageIndex{2}\) presenta los mismos puntajes de los aspirantes de empleo, pero ahora están codificados por colores por pertenencia al grupo (es decir, a qué grupo pertenecen). Ahora que podemos diferenciar entre aspirantes de esta manera, comienza a surgir un patrón: aquellos aspirantes con un grado relevante (codificado en rojo) tienden a estar cerca de la parte superior, los aspirantes sin título universitario (codificado en negro) tienden a estar cerca de la parte inferior, y los aspirantes con un grado no relacionado (codificado en verde) tienden a caer en el medio. Sin embargo, incluso dentro de estos grupos, todavía hay cierta variabilidad, como se muestra en la Figura\(\PageIndex{2}\).
Este patrón es aún más fácil de ver cuando los aspirantes son ordenados y organizados en sus respectivos grupos, como se muestra en la Figura\(\PageIndex{3}\).

Ahora que tenemos nuestros datos visualizados en un formato fácilmente interpretable, podemos ver claramente que las puntuaciones de nuestros solicitantes difieren en gran medida a lo largo de las líneas de grupo. Aquellos aspirantes que no cuentan con un título universitario recibieron los puntajes más bajos, los que tenían un título relevante para el trabajo recibieron los puntajes más altos, y los que sí tenían un título pero uno que no está relacionado con el trabajo tendieron a caer en algún lugar en el medio. Así, tenemos varianza sistemática entre nuestros grupos.
También podemos ver claramente que dentro de cada grupo, los puntajes de nuestros solicitantes diferían entre sí. Aquellos aspirantes sin titulación tendían a anotar de manera muy similar, ya que los puntajes se agrupan muy juntos. Nuestro grupo de aspirantes con títulos relevantes varió un poco pero más que eso, y nuestro grupo de aspirantes con títulos no relacionados varió bastante. Puede ser que haya otros factores que provoquen las diferencias de puntuación observadas dentro de cada grupo, o simplemente podrían deberse a una probabilidad aleatoria. Debido a que no tenemos ningún otro dato explicativo en nuestro conjunto de datos, la variabilidad que observamos dentro de nuestros grupos se considera error aleatorio, con cualquier desviación entre una persona y la media del grupo de esa persona causada solo por casualidad. Así, tenemos varianza no sistemática (aleatoria) dentro de nuestros grupos.
El proceso y los análisis utilizados en ANOVA tomarán estas dos fuentes de varianza (varianza sistemática entre grupos y error aleatorio dentro de los grupos, o cuánto se diferencian los grupos entre sí y cuánto difieren las personas dentro de cada grupo) y las compararán entre sí para determinar si los grupos tienen alguna explicación valor en nuestra variable de resultado. Al hacer esto, probaremos diferencias estadísticamente significativas entre las medias grupales, al igual que hicimos para\(t\) las pruebas. Iremos paso a paso para desglosar las matemáticas para ver cómo funciona realmente el ANOVA.


