3.6.2: Coeficiente de correlación
- Page ID
- 151806
El coeficiente de correlación (representado por la letra\(r\)) mide tanto la dirección como la fuerza de una relación lineal o asociación entre dos variables. El valor siempre\(r\) tomará un valor entre ‐1 y 1. Los valores cercanos a cero indican una correlación muy débil. Valores cercanos a 1 o ‐1 indican una correlación muy fuerte. El coeficiente de correlación no debe utilizarse para la correlación no lineal.
Es importante ignorar el signo a la hora de determinar la fuerza de correlación. Por ejemplo,\(r = ‐0.75\) indicaría una correlación más fuerte que\(r = 0.62\), ya que ‐0.75 está más lejos de cero.
Utilizaremos la tecnología para calcular el coeficiente de correlación, pero al final de esta sección se\(r\) presentan fórmulas para calcular manualmente.
Interpretación del coeficiente de correlación (\(r\))
\[-1 \leq r \leq 1 \nonumber \]
\(r = 1\)significa correlación positiva perfecta
\(r = ‐1\)significa correlación negativa perfecta
\(r = 0\)significa que no hay correlación
Cuanto más lejos\(r\) está de cero, más fuerte es la correlación
\(r > 0\)significa correlación positiva
\(r < 0\)significa correlación negativa
Algunos Ejemplos
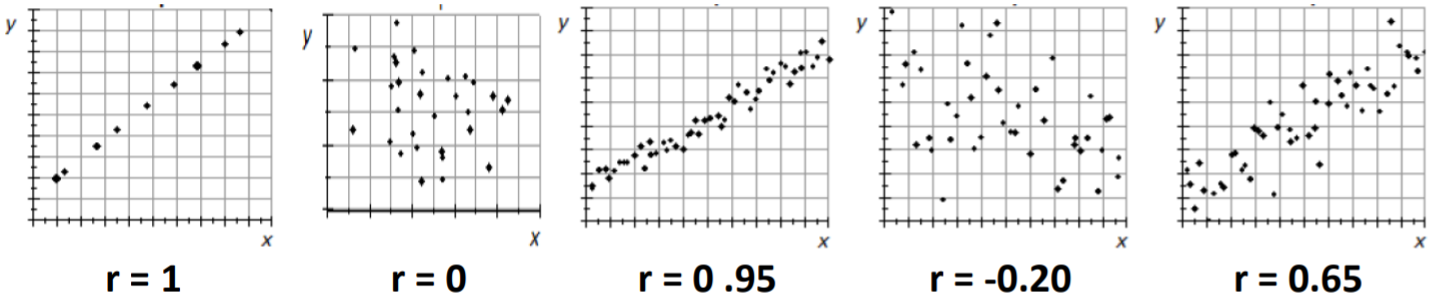
Ejemplo: Rendimiento de pepino y precipitación
Esta gráfica de dispersión representa datos recolectados aleatoriamente sobre la precipitación de la temporada de crecimiento y el rendimiento de pepino
\(r= 0.871\)lo que indica una fuerte correlación positiva.
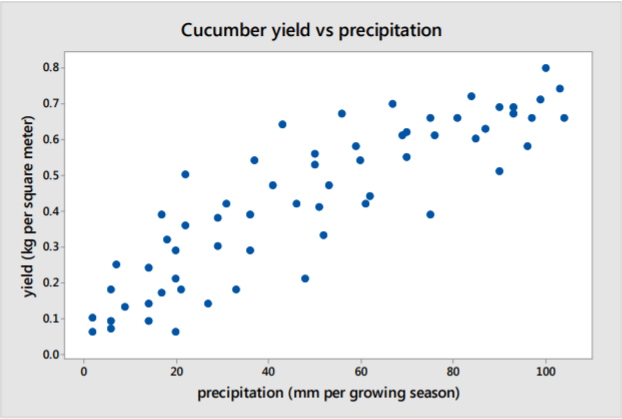
Ejemplo: GPA y clase faltante
Un grupo de estudiantes de Georgia College realizó una encuesta en la que se hacían varias preguntas a los estudiantes al azar sobre su perfil académico. Una parte de su estudio fue ver si existe alguna correlación entre el GPA de varios estudiantes y las clases perdidas.
\(r= ‐0.236\)lo que indica débil correlación negativa.
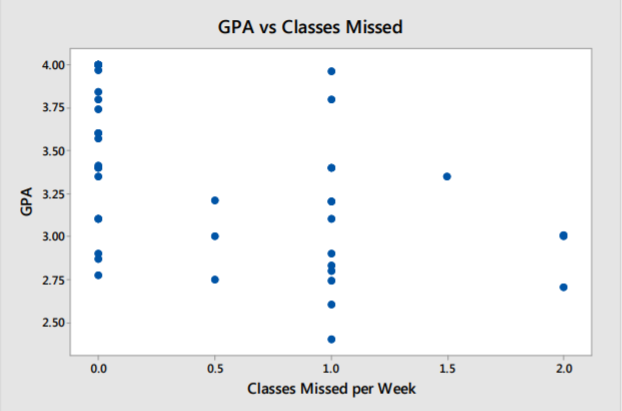
Ejemplo: Tiempos de viaje y temperatura
Un instructor de matemáticas conmuta en automóvil desde su casa en San Francisco al Colegio De Anza en Cupertino, California. Durante 100 días seleccionados al azar durante el año, el instructor registró el tiempo de desplazamiento y la temperatura en Cupertino al momento de su llegada.
\(r = ‐0.02\)indicando que no hay correlación.
Cálculo del coeficiente de correlación
Calcular manualmente el coeficiente de correlación es un proceso tedioso, pero aquí se presentan las fórmulas necesarias y un ejemplo sencillo:
Fórmulas para calcular el coeficiente de correlación (\(r\))
\[r=\dfrac{S S X Y}{\sqrt{S S X \cdot S S Y}} \nonumber \]
\[S S X=\Sigma X^{2}-\dfrac{1}{n}(\Sigma X)^{2} \nonumber \]
\[S S Y=\Sigma Y^{2}-\dfrac{1}{n}(\Sigma Y)^{2} \nonumber \]
\[S S X Y=\Sigma X Y-\dfrac{1}{n}(\Sigma X \cdot \Sigma Y) \nonumber \]
Ejemplo: Venta de gafas de sol y lluvia
Una empresa de venta de gafas de sol determinó las unidades vendidas por cada 1000 personas y la precipitación anual en 5 ciudades.
X = precipitación en pulgadas
Y = venta de gafas de sol por cada 1000 personas.
| X | Y |
|---|---|
| 10 | 40 |
| 15 | 35 |
| 20 | 25 |
| 30 | 25 |
| 40 | 15 |
Solución
Primero, encuentra las siguientes sumas:
\[\sum X, \sum Y, \sum X^{2}, \sum Y^{2}, \sum X Y \nonumber \]
| \(X)\) | \(Y\) | \(X^{2}\) | \(Y^{2}\) | \(XY\) | |
|---|---|---|---|---|---|
| \ (X)\)” class="lt-estados-20845">10 | \ (Y\)” class="lt-estados-20845">40 | \ (X^ {2}\)” class="lt-stats-20845">100 | \ (Y^ {2}\)” class="lt-stats-20845">1600 | \ (XY\)” class="lt-estados-20845">400 | |
| \ (X)\)” class="lt-estados-20845">15 | \ (Y\)” class="lt-estados-20845">35 | \ (X^ {2}\)” class="lt-stats-20845">225 | \ (Y^ {2}\)” class="lt-stats-20845">1225 | \ (XY\)” class="lt-estados-20845">525 | |
| \ (X)\)” class="lt-estados-20845">20 | \ (Y\)” class="lt-estados-20845">25 | \ (X^ {2}\)” class="lt-stats-20845">400 | \ (Y^ {2}\)” class="lt-stats-20845">625 | \ (XY\)” class="lt-estados-20845">500 | |
| \ (X)\)” class="lt-estados-20845">30 | \ (Y\)” class="lt-estados-20845">25 | \ (X^ {2}\)” class="lt-stats-20845">900 | \ (Y^ {2}\)” class="lt-stats-20845">625 | \ (XY\)” class="lt-estados-20845">750 | |
| \ (X)\)” class="lt-estados-20845">40 | \ (Y\)” class="lt-estados-20845">15 | \ (X^ {2}\)” class="lt-stats-20845">1600 | \ (Y^ {2}\)” class="lt-stats-20845">225 | \ (XY\)” class="lt-estados-20845">600 | |
| \(\mathbf{\Sigma}\) | \ (X)\)” class="lt-estados-20845"> 115 | \ (Y\)” class="lt-estados-20845"> 140 | \ (X^ {2}\)” class="lt-stats-20845"> 3225 | \ (Y^ {2}\)” class="lt-stats-20845"> 4300 | \ (XY\)” class="lt-estados-20845"> 2775 |
Entonces, encontrar\(SSX\),\(SSY\),\(SSXY\)
\ (\ begin {array} {ll}
S X=3225-115^ {2}/5 & =580\\
S S Y=4300-140^ {2}/5 & =380\\
S S X Y=2775- (115) (140)/5 & =-445
\ end {array}\)
Por último, calcule\(r\)
\(r=\dfrac{S S X Y}{\sqrt{S S X \cdot S S Y}}=\dfrac{-445}{\sqrt{580 \cdot 330}}=-0.9479\)
El coeficiente de correlación es ‐0.95, lo que indica una correlación fuerte y negativa entre la lluvia y la venta de gafas de sol.


