5.5: Probabilidad conjunta y regla aditiva
- Page ID
- 151811
Dos o más eventos se pueden combinar en eventos conjuntos mediante el uso de declaraciones “o” o declaraciones “y”.
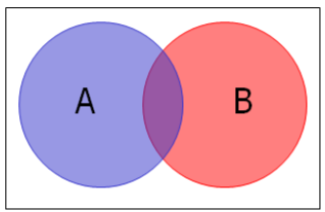
La Unión de dos eventos A y B es que ocurre cualquiera de los eventos A o B, o ambos; (las partes azul, rojo y morado del diagrama de Venn se muestran a la derecha).
La Intersección de dos eventos A y B es que ambos eventos A y B ocurren; (la superposición púrpura del diagrama de Venn se muestra a la derecha).
Probabilidad marginal significa la probabilidad de que ocurra un solo evento.
Probabilidad conjunta significa la probabilidad de que ocurra la unión o intersección de múltiples eventos.
Ejemplo: Cursos para estudiantes
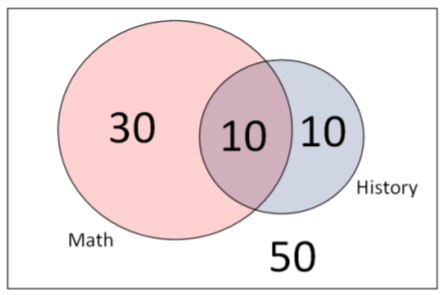
En un grupo de 100 estudiantes, un total de 40 estudiantes toman Matemáticas, un total de 20 estudiantes toman Historia y 10 estudiantes toman tanto Matemáticas como Historia. (Tenga en cuenta que estos 10 alumnos ya se contabilizaron dos veces como estudiantes de Matemáticas y estudiantes de Historia). Encuentra las probabilidades marginales y articulares.
Solución
Probabilidades Marginales:
P (Matemáticas) = 40/100 = 0.4
P (Historial) = 20/100 = 0.2
Probabilidades articulares:
P (Matemáticas e Historia) = 10/100 = 0.1 (esta es la intersección de los dos eventos)
P (Matemáticas o Historia) = 50/100 = 0.5 (esta es la unión de los dos eventos)
Podemos hacer una regla para relacionar probabilidades conjuntas y marginales pero notando que estamos contando dos veces los resultados en la intersección de dos eventos al combinar probabilidades marginales de evento cada evento. A esto se le llama la Regla Aditiva.
La regla aditiva para la probabilidad
\[P(A \text { or } B)=P(A)+P(B)-P(A \text { and } B) \nonumber \]
Ejemplo: Cursos para estudiantes
Calcular la probabilidad de que un estudiante esté tomando Matemáticas o Historia usando la regla aditiva. Comparar con el cálculo directo del ejemplo anterior.
Solución
P (Matemáticas o Historia) = P (Matemáticas) + P (Historia) — P (Matemáticas o Historia)
P (Matemáticas o Historia) = 0.4 + 0.2 — 0.1 = 0.5
Mutuamente Exclusivos significa que dos eventos A, B no pueden ocurrir ambos. En este caso, la intersección de dos eventos no tiene resultados posibles.
La regla aditiva para eventos mutuamente excluyentes
\[P(A \text { or } B)=P(A)+P(B) \nonumber \]
Ejemplo: Clase de español
500 estudiantes de un colegio comunitario están tomando español 1A en el trimestre de otoño de este año. 32 estudiantes están en la Sección 11 y 30 estudiantes están en la Sección 12. Encuentra la probabilidad de que un estudiante español 1A esté en las Secciones 11 o en la Sección 12.
Solución
Dado que los estudiantes no pueden estar en dos secciones de la misma clase, los eventos Sección 11 y Sección 12 son mutuamente excluyentes.
P (Sec 11 o 12) = P (Sec 11) + P (Sec 12) = 32/500 + 30 /500 = 62/500 = 0.124


