10.4: Recopilar y analizar datos experimentales
- Page ID
- 151722
Después de diseñar el experimento, entonces recolectaríamos y verificaríamos los datos. A los efectos del análisis estadístico, asumiremos que todo el muestreo es aleatorio o utiliza una técnica alternativa que simula adecuadamente una muestra aleatoria.
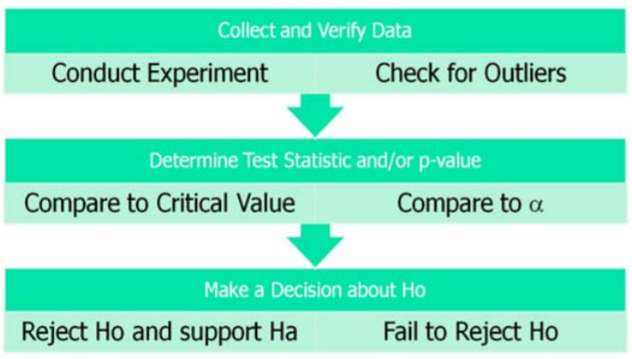
Verificación de datos
Después de recopilar los datos pero antes de ejecutar la prueba, necesitamos verificar los datos. Primero, obtener una imagen de los datos haciendo una gráfica (histograma, gráfica de puntos, gráfica de caja, etc.). Verifique la asimetría, la forma y cualquier valor atípico potencial en los datos.
Trabajar con valores atípicos
Un valor atípico es un punto de datos que está muy alejado de las otras entradas del conjunto de datos. Los valores atípicos podrían ser causados por:
- Errores cometidos en la grabación de datos
- Datos que no pertenecen a la población
- Verdaderos eventos raros
Los dos primeros casos son sencillos de tratar ya que podemos corregir errores o eliminar datos que no pertenecen a la población. El tercer caso es más problemático ya que los valores atípicos extremos aumentarán drásticamente la desviación estándar y sesgarán fuertemente los datos.
En El cisne negro, Nicholas Taleb sostiene que algunas poblaciones con valores atípicos extremos no deben analizarse con intervalos de confianza tradicionales y pruebas de hipótesis. 72 Define a un Cisne Negro como un valor atípico extremo impredecible que causa efectos dramáticos en la población. Un ejemplo reciente de Cisne Negro fue la catastrófica caída en el valor de las inversiones no reguladas en seguros inmobiliarios de Credit Default Swap (CDS) que provocó el casi colapso del sistema bancario internacional en 2008. El análisis estadístico tradicional que midió el riesgo de las inversiones de CDS no tomó en cuenta la consecuencia de un rápido incremento en el número de ejecuciones hipotecarias de viviendas. En este caso, las estadísticas que miden el desempeño de la inversión y el riesgo fueron inútiles y crearon una falsa sensación de seguridad para los grandes bancos y compañías de seguros.
Ejemplo: ventas de casas de bienes raíces
Aquí están las ventas trimestrales de viviendas para 10 agentes inmobiliarios
2 2 3 4 5 5 6 6 7 50
| Con valores atípicos | Sin valores atípicos | |
|---|---|---|
| Media | 9.00 | 4.44 |
| Mediana | 5.00 | 5.00 |
| Desviación estándar | 14.51 | 1.81 |
| Gama Intercuartil | 3.00 | 3.50 |
En este ejemplo, el número 50 es un valor atípico. Al calcular las estadísticas resumidas, podemos ver que la media y la desviación estándar se ven dramáticamente afectadas por el valor atípico, mientras que la mediana y el rango intercuartílico (que se basan en el ranking de los datos) apenas cambian. Una solución cuando se trata de una población con valores atípicos extremos es usar estadísticas inferenciales usando los rangos de los datos, también llamados estadísticas no paramétricas.
Uso de Box Plot para encontrar valores atípicos
- La “caja” es la región entre los cuartiles 1 y 3.
- Los posibles valores atípicos son más de 1.5 IQR de la caja (cerca interior)
- Los valores atípicos probables son más de 3 IQR de la caja (cerca exterior)
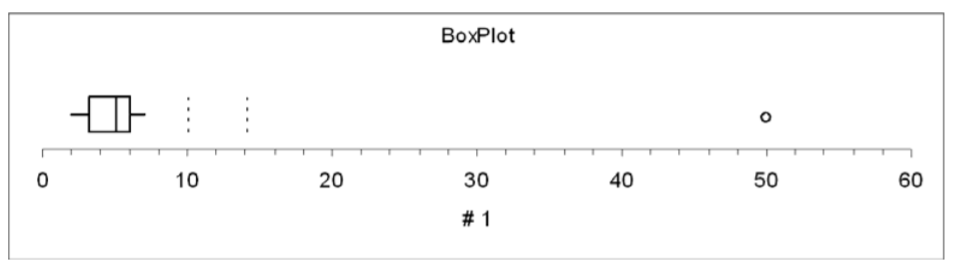
- En la gráfica de cuadro a continuación, que ilustra el ejemplo del agente inmobiliario, las líneas punteadas representan las “cercas” que son 1.5 y 3 IQR de la caja. Vea cómo el punto de datos 50 está bien fuera de la cerca exterior y por lo tanto un valor atípico casi seguro.
La lógica de las pruebas de hipótesis
Después de verificar los datos, queremos llevar a cabo la prueba de hipótesis y llegar a una decisión: rechazar o no la Hipótesis Null. El proceso de decisión es similar a una “prueba por contradicción” utilizada en matemáticas:
- Asumimos que Ho es cierto antes de observar los datos y el diseño\(H_{a}\) para ser el complemento de\(H_{o}\).
- Observar los datos (evidencia). ¿Qué tan inusuales están bajo estos datos\(H_{o}\)?
- Si los datos son demasiado inusuales, hemos “probado”\(H_{o}\) es falso: rechazar\(H_{o}\) y apoyar\(H_{a}\) (declaración fuerte).
- Si los datos no son demasiado inusuales, fallamos en rechazar\(H_{o}\). Esto no “prueba” nada y decimos que los datos no son concluyentes. (declaración débil).
- Nunca podremos “probarlo”\(H_{o}\), sólo “desmentirlo”.
- “Probar” en estadística significa soporte con (\(1-\alpha\)) 100% de certeza. (ejemplo: si\(\alpha =.05\), entonces tenemos al menos un 95% de confianza en nuestra decisión de rechazar\(H_{o}\).
Regla de Decisión — Dos métodos, Misma Decisión
Anteriormente se introdujo la idea de un estadístico de prueba que es un valor calculado a partir de los datos bajo el Modelo Estadístico apropiado a partir de los datos que se pueden comparar con el valor crítico de la prueba de Hipótesis. Si el estadístico de prueba cae en la región de rechazo del modelo estadístico, rechazamos la Hipótesis Null.
Recordemos que el valor crítico se determinó por diseño sobre la base del nivel de significación elegido\(\alpha\). El método más preferido para tomar decisiones es calcular la probabilidad de obtener un resultado tan extremo como el valor del estadístico de prueba. Esta probabilidad se llama el \(p\)‐valor, y se puede comparar directamente con el nivel de significancia.
Definición:\(p\)-value
\(p\)‐value: la probabilidad, asumiendo que la hipótesis nula es verdadera, de obtener un valor del estadístico de prueba al menos tan extremo como el valor calculado para la prueba.
- Si el\(p\) valor ‐es menor que el nivel de significancia\(\alpha\),\(H_o\) se rechaza.
- Si el\(p\) valor ‐es mayor que el nivel de significancia\(\alpha\), no\(H_o\) se rechaza.
Comparando\(p\) ‐valor con\(\alpha\)
Tanto el\(p\) ‐value como\(\alpha\) son probabilidades de obtener resultados tan extremos como los datos asumiendo que\(H_o\) es cierto.
El\(p\) ‐valor está determinado por los datos y está relacionado con la probabilidad real de cometer un error de Tipo I (rechazando una verdadera Hipótesis Null). Cuanto menor sea el\(p\) valor ‐, menor será la probabilidad de cometer un error de Tipo I y, por lo tanto, más probabilidades hay de rechazar la Hipótesis Null.
El nivel de significancia\(\alpha\) está determinado por el diseño y es la probabilidad máxima que estamos dispuestos a aceptar de rechazar un verdadero\(H_o\).
- Si el estadístico de prueba se encuentra en la región de rechazo, rechace\(H_o\). (método de valor crítico)
- Si el\(p\) ‐valor <\(\alpha\), rechazar\(H_o\). (método\(p\) del ‐valor)
Este método de comparación\(p\) ‐value se prefiere al método del valor crítico porque la regla es la misma para todos los modelos estadísticos: Rechazar\(H_o\) si\(p\) ‐valor <\(\alpha\).
Veamos por qué estas dos reglas son equivalentes analizando una prueba de media vs. valor hipotético.
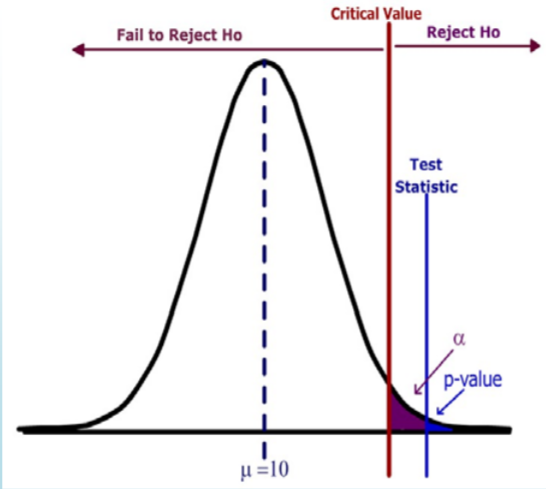
- \( H_o: \mu=10 \qquad H_a: \mu > 10\)
- Diseño: El valor crítico está determinado por el nivel de significancia\(\alpha\).
- Análisis de datos: el valor p se determina mediante el estadístico de prueba
- El estadístico de prueba cae en la región de rechazo.
- \(p\)‐valor (azul) <\(\alpha\) (púrpura)
- Rechazar\(H_o\).
- Declaración fuerte: Los datos apoyan la hipótesis alternativa.
En este ejemplo, el estadístico de prueba se encuentra en la región de rechazo (el área a la derecha del valor crítico). El\(p\) ‐valor (el área a la derecha del estadístico de prueba) es menor que el nivel de significancia (el área a la derecha del valor crítico). La decisión es Rechazar\(H_o\).
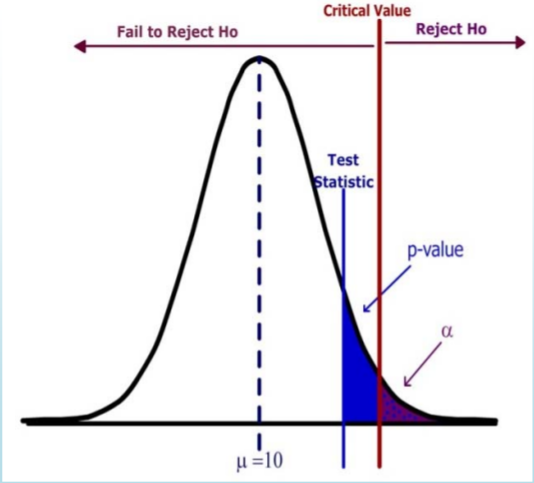
- \( H_o: \mu=10 \qquad H_a: \mu > 10\)
- Diseño: el valor crítico está determinado por el nivel de significancia\(\alpha\).
- Análisis de datos:\(p\) ‐valor se determina por estadística de prueba
- El estadístico de prueba no cae en la región de rechazo.
- \(p\)‐valor (azul) >\(\alpha\) (púrpura)
- No Rechazar\(H_o\).
- Declaración débil: Los datos no son concluyentes y no apoyan la Hipótesis Alternativa.
En este ejemplo, la Estadística de Prueba no se encuentra en la Región de Rechazo. El\(p\) ‐valor (el área a la derecha del estadístico de prueba) es mayor que el nivel de significancia (el área a la derecha del valor crítico). La decisión es No Rechazar\(H_o\).


