14.1: Revisión de Datos Bivariados y Gráficas de Dispersión
- Page ID
- 151914
En el Capítulo 3, definimos los datos bivariados como datos que tienen dos variables numéricas diferentes. En una clase de álgebra, estos también se conocen como pares ordenados. Dejaremos que X represente la variable independiente (o explicativa) e Y representará la variable dependiente (o respuesta) en esta definición. Aquí un ejemplo de cinco pares totales en los que X representa la precipitación anual en pulgadas en una ciudad e Y representa las ventas anuales de gafas de sol por cada 1000 habitantes.
La mejor manera de graficar datos bivariados es mediante el uso de un Scatterplot en el que X, la variable independiente es el eje vertical e Y, la variable dependiente es el eje horizontal.
Aquí hay un ejemplo y diagrama de dispersión de cinco pares totales donde X representa la precipitación anual en pulgadas en una ciudad e Y representa las ventas anuales de gafas de sol por cada 1000 habitantes.
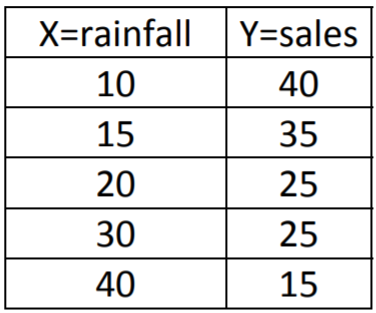
Solución
En la gráfica de dispersión para estos datos, parece que las ciudades con más precipitaciones tienen menores ventas. También parece que esta relación es lineal, patrón que luego puede ejemplificarse en un modelo estadístico.