14.2: El Modelo de Regresión Lineal Simple
- Page ID
- 151925
En el ejemplo de diagrama de dispersión mostrado anteriormente, vimos correlación lineal entre las dos variables dependientes. Ahora vamos a crear un modelo estadístico que relacione estas dos variables, pero comencemos revisando un modelo lineal matemático a partir del álgebra:
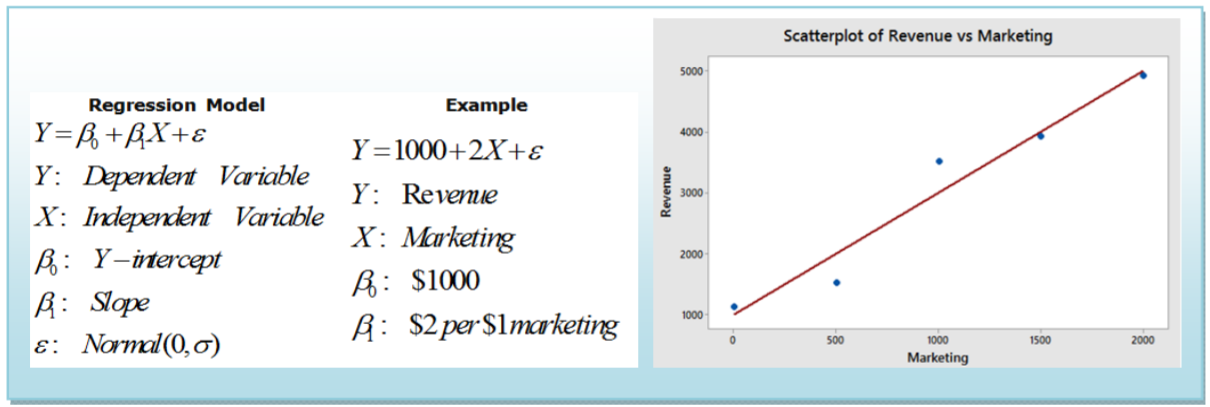
\(Y=\beta_{0}+\beta_{1} X\)
\(Y\): Variable dependiente
\(X\): Variable independiente
\(\beta_{0}\): Y - intercepción
\(\beta_{1}\):Talud
Tienes una pequeña empresa que produce camisetas personalizadas. Sin marketing, tu negocio tiene ingresos (ventas) de $1000 por semana. Cada dólar que gastes mercadotecnia aumentará los ingresos en 2 dólares. Deje que la\(X\) variable represente la cantidad gastada en marketing y que la variable\(Y\) represente los ingresos por semana. Escribir un modelo matemático que se\(X\) relacione con\(Y\).
Solución
En este ejemplo, estamos diciendo que los ingresos semanales (\(Y\)) dependen del gasto de marketing (\(X\)). $1000 de ingresos semanales representan la intercepción vertical, y $2 de ingresos semanales por $1 comercialización representa la pendiente, o tasa de cambio del modelo. Podemos elegir algún valor de\(X\) y determinar\(Y\) y luego trazar los puntos en una gráfica de dispersión para ver esta relación lineal.
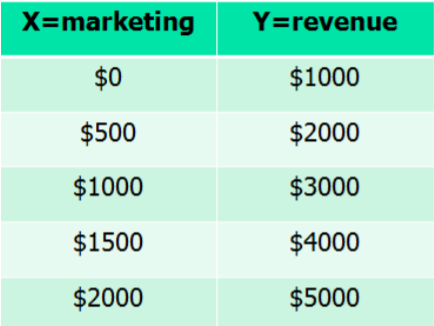
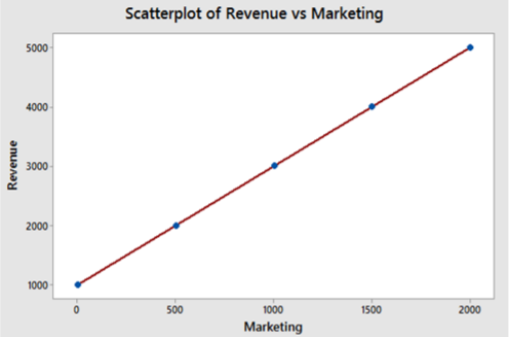
Luego podemos escribir el modelo lineal matemático como una ecuación:

Todos aprendimos sobre estos modelos lineales en clases de Álgebra, pero el mundo real generalmente no da resultados tan perfectos. En particular, podemos elegir qué gastar en marketing, pero los ingresos reales tendrán más incertidumbre. Por ejemplo, los verdaderos ingresos pueden verse más así:
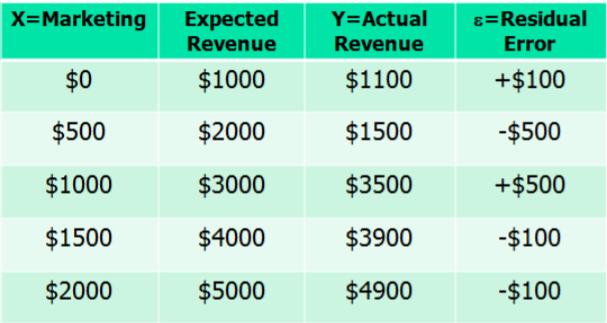
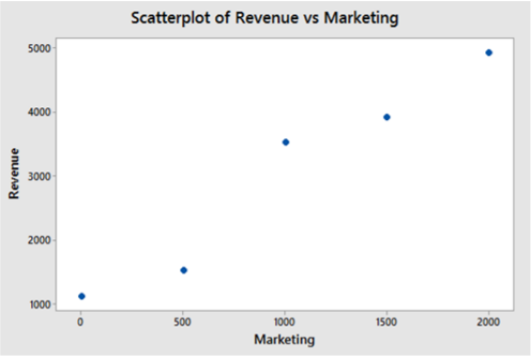
La diferencia entre los ingresos reales y los ingresos esperados se denomina el error residual,\(\varepsilon\) si asumimos que el error residual (representado por\(\varepsilon\)) es una variable aleatoria que sigue una distribución normal con\(\mu=0\) y\(\sigma\) una constante para todos los valores de \(X\), ahora hemos creado un modelo estadístico llamado modelo de regresión lineal simple.