14.9: Análisis Residual
- Page ID
- 151889
En regresión, asumimos que el modelo es lineal y que los errores residuales (\(Y-\hat{Y}\)para cada par) son aleatorios y normalmente distribuidos. Podemos analizar los residuos para ver si estos supuestos son válidos y si existen posibles valores atípicos. En particular:
- Los residuos deben representar un modelo lineal.
- El error estándar (desviación estándar de los residuos) no debe cambiar cuando el valor de\(X\) los cambios.
- Los residuos deben seguir una distribución normal.
- Busque cualquier valor extremo potencial de\(X\).
- Busque cualquier error residual extremo.
El modelo A es un ejemplo de un modelo de regresión lineal apropiado. Haremos tres gráficas para probar el residuo; una gráfica de dispersión con la línea de regresión, una gráfica de los residuos y un histograma de los residuos
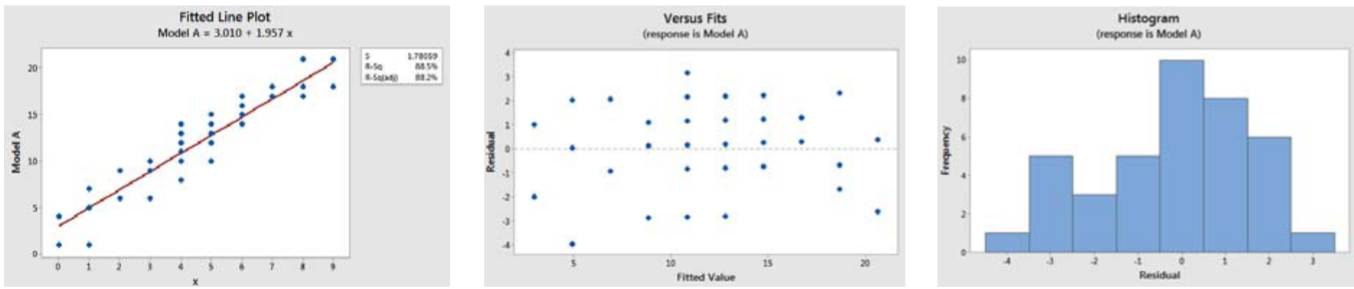
Aquí podemos ver el que los residuos parecen ser aleatorios, el ajuste es lineal, y el histograma tiene aproximadamente forma de campana. Además, no hay valores atípicos extremos\(X\) ni residuos atípicos.
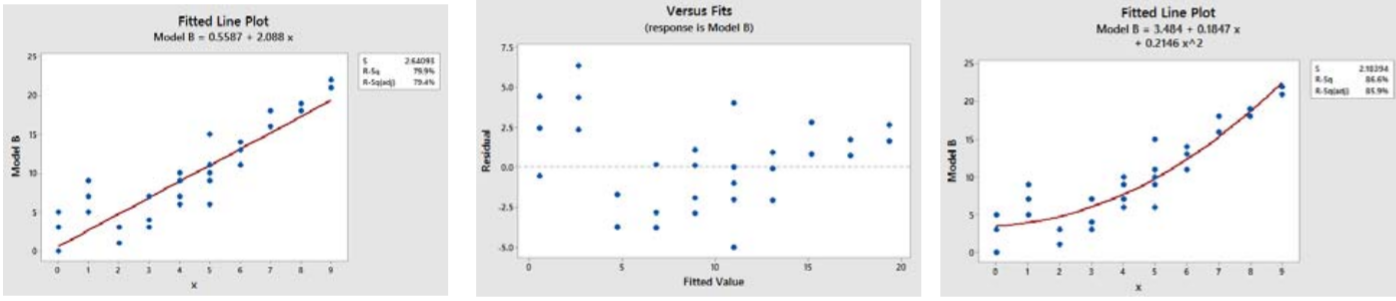
El modelo B parece un ajuste fuerte, pero los residuales están mostrando un patrón de ser positivo para valores bajos y altos de\(X\) y negativos para valores medios de\(X\). Esto indica que el modelo no es lineal y debe ajustarse con un modelo de regresión no lineal (por ejemplo, la tercera gráfica muestra un modelo cuadrático).
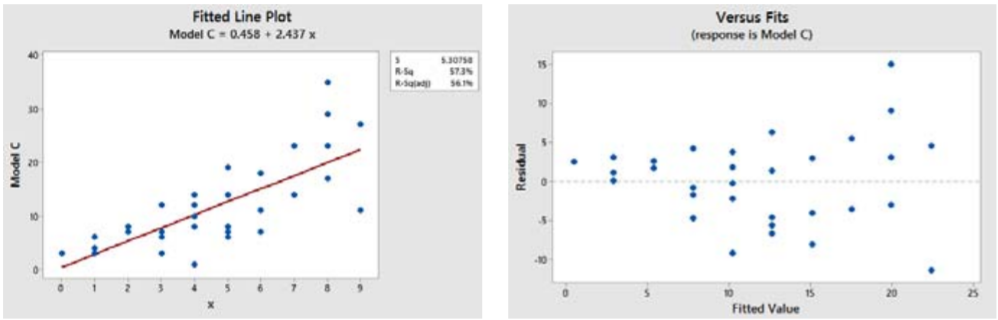
El modelo C tiene un ajuste lineal, pero los residuales están mostrando un patrón de ser más pequeños para valores bajos de\(X\) y mayores para valores grandes de\(X\). Esto viola la suposición de que el error estándar no debe cambiar cuando el valor de\(X\) los cambios. Este fenómeno se denomina heterocedasticidad y requiere una transformación de datos para encontrar un modelo más apropiado.
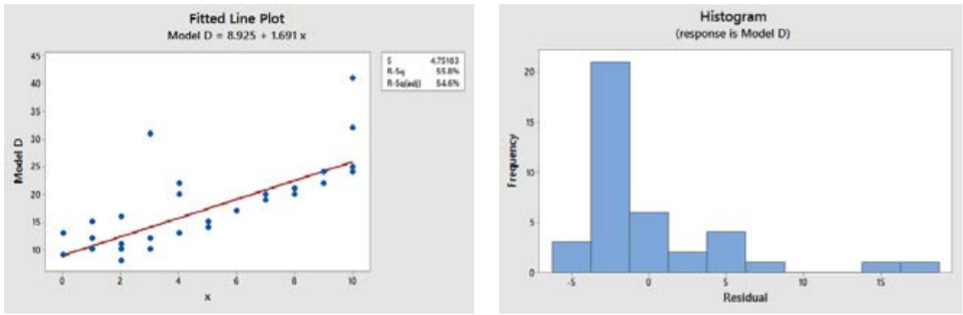
El modelo D parece tener un ajuste lineal, pero los residuales están mostrando un patrón de ser más grandes cuando son positivos y más pequeños cuando son negativos. Esto viola el supuesto de que los residuos deben seguir una distribución normal, como puede verse en el histograma.
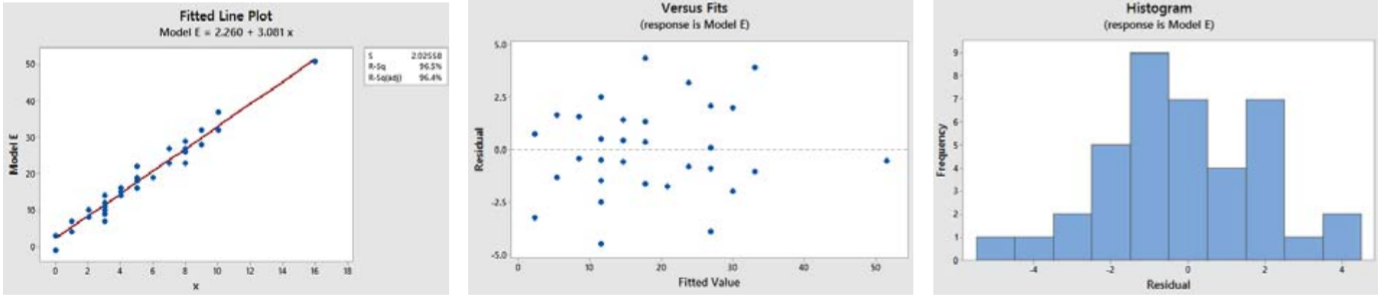
El modelo E parece tener un ajuste lineal, y los residuos parecen aleatorios y normales. Sin embargo, el valor (16,51) es un valor atípico extremo de\(X\) y puede tener una influencia indebida en la elección de la línea de regresión.
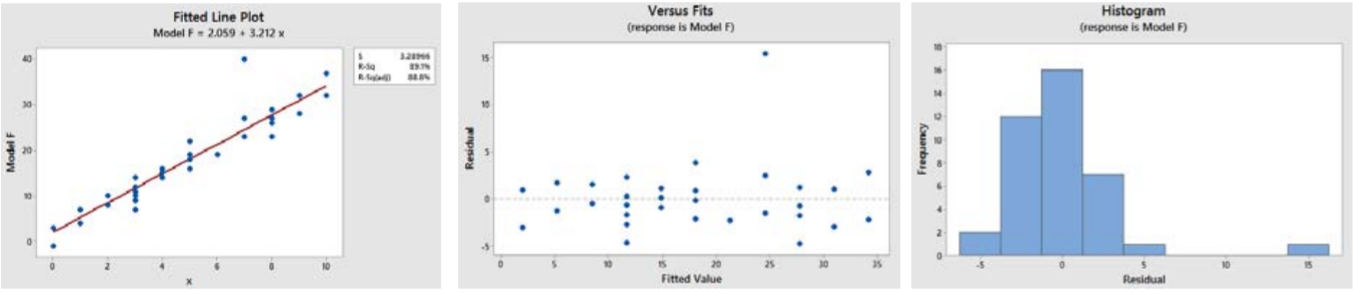
El modelo F parece tener un ajuste lineal, y los residuales parecen aleatorios y normales, excepto por un valor atípico en el valor (7,40). Este valor atípico es diferente al valor atípico extremo en el Modelo E, pero seguirá teniendo una influencia indebida en la elección de la línea de regresión.


