15.2.4: Capítulo 5 Tareas
- Page ID
- 151441
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
- En el juego de Dados, se tiran dos dados y se suma la suma. Un conjunto de 4 apuestas se llama “hard ways”, en el que el jugador tiene que rodar el número en dobles antes de que se emita una versión 7 o una versión no dura del número. Por ejemplo, supongamos que quiere apostar por la manera dura 6. Para ganar, debes tirar un par de tres antes de rodar un siete o cualquier otra combinación que sume a 6. Todos los demás rollos son ignorados.

- Para el camino difícil 6, enumere el espacio de muestra de rollos que tienen un efecto en el juego. Entonces encuentra la probabilidad de ganar.
- Para el camino duro 4, enumere el espacio de muestra de rollos que tienen un efecto en el juego. Entonces encuentra la probabilidad de ganar.
- Por el camino duro 4, el casino pagará de 7 a 1 si ganas. Por el camino duro 6, el casino pagará de 9 a 1 si ganas. Compara el pago con las cuotas reales. ¿El casino tiene una ventaja en este juego?
- El 40% de los estudiantes de un colegio comunitario reciben ayuda económica. El 30% de los estudiantes de la misma universidad vive con al menos uno de sus padres. El 15% de los estudiantes reciben ayuda económica y viven con al menos uno de los padres.
- Encuentra la probabilidad de que un estudiante de un colegio comunitario no viva con al menos uno de los padres. ¿Es esta probabilidad marginal, conjunta o condicional?
- Encuentra la probabilidad de que un estudiante de un colegio comunitario esté recibiendo ayuda económica o viva con al menos uno de los padres. ¿Es esta probabilidad marginal, conjunta o condicional?
- Encuentra la probabilidad de que un estudiante de un colegio comunitario que vive con al menos uno de los padres también esté recibiendo ayuda económica. ¿Es esta probabilidad marginal, conjunta o condicional?
- Politico/Morning Consult realizó una encuesta de votantes registrados estadounidenses en noviembre de 2017 tras el tiroteo masivo de Las Vegas, en el que 58 asistentes al concierto fueron asesinados por un solo pistolero. El sondeo hizo la pregunta: “¿Apoya u se opone a leyes de armas más estrictas en Estados Unidos? Los resultados de la encuesta, tabulados cruzadamente por género, se muestran en la tabla de contingencia.
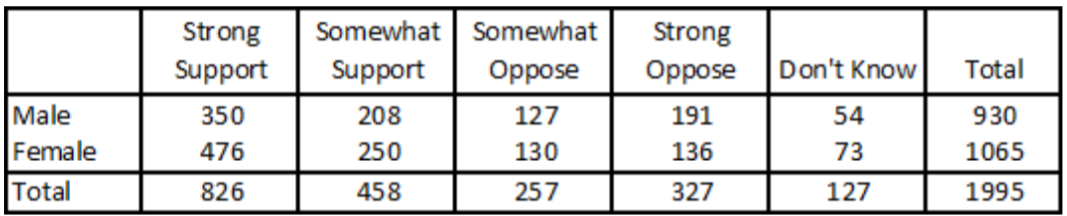
- ¿Qué porcentaje de todos los votantes registrados apoya (fuertes o algo) leyes de armas más estrictas?
- ¿Qué porcentaje de varones apoya (fuertes o algo) leyes de armas más estrictas?
- ¿Qué porcentaje de mujeres apoyan (fuertes o algo) leyes de armas más estrictas?
- ¿Son eventos independientes el género y el apoyo a leyes de armas más estrictas? Explicar
- Un estudiante tiene un 90% de posibilidades de llegar a clase a tiempo el lunes y un 70% de posibilidades de llegar a clase a tiempo el martes. Suponiendo que se trata de eventos independientes, determine las siguientes probabilidades:
- El alumno es puntual tanto el lunes como el martes.
- El alumno llega a tiempo al menos una vez (lunes o martes).
- El alumno llega tarde ambos días.
- Una clase cuenta con 10 alumnos, 6 mujeres y 4 varones. Se muestreará a 3 estudiantes sin reemplazo para una presentación grupal.
- Construir un diagrama de árbol de todas las posibilidades (habrá 8 ramas totales al final)
- Encuentra las siguientes probabilidades:
- Todos los estudiantes varones en la presentación grupal.
- Exactamente 2 alumnas en la presentación grupal.
- Al menos 2 alumnas en la presentación grupal.
- El 20% de los ciclistas profesionales están usando un medicamento para mejorar el rendimiento. Se ha desarrollado una prueba para el medicamento; esta prueba tiene un 60% de probabilidad de detectar correctamente el medicamento (verdadero positivo). No obstante, la prueba saldrá positiva en 2% de los ciclistas que no usan el medicamento (falso positivo).
- Construir un diagrama de árbol en el que el primer conjunto de ramas sean ciclistas con y sin la droga, y el segundo conjunto sea si dan positivo.
- A partir del diagrama de árbol, cree una tabla de contingencia.
- ¿Qué porcentaje de ciclistas dará positivo por el medicamento?
- Si un ciclista da positivo, ¿cuál es la probabilidad de que el ciclista haya consumido realmente la droga?
- El 1% de la población de un país tiene la enfermedad X. Se ha desarrollado una prueba para la enfermedad; esta prueba tiene una probabilidad del 95% de detectar correctamente la enfermedad (verdadero positivo). No obstante, la prueba saldrá positiva en 2% de las personas que no tienen la enfermedad X (falso positivo).
- Construir un diagrama de árbol en el que el primer conjunto de ramas sean personas con y sin la enfermedad, y el segundo conjunto sea si dan positivo. Asignar probabilidades a cada opción.
- A partir del diagrama de árbol, cree una tabla de contingencia con una base de 10000
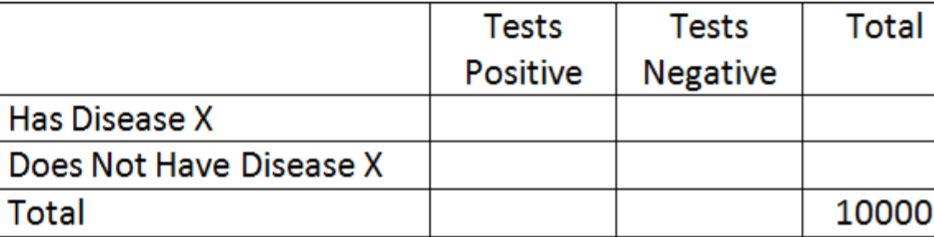
- ¿Qué porcentaje de la población dará positivo para la enfermedad X?
- Si una persona da positivo, ¿cuál es la probabilidad de que la persona realmente tenga la enfermedad X?
- Deseamos determinar la moral de una determinada empresa. Damos a cada uno de los trabajadores un cuestionario, y a partir de sus respuestas podemos determinar el nivel de su moral, ya sea 'Bajo', 'Medio' o 'Alto: también se señala a continuación el 'tipo de trabajo' para cada uno de los trabajadores. Para cada tipo de trabajador, a continuación se dan las frecuencias correspondientes a los diferentes niveles de moral.
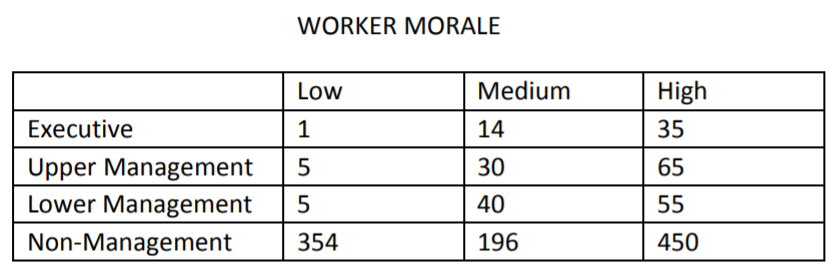
- Seleccionamos al azar 1 trabajador de esta población. ¿Cuál es la probabilidad de que el trabajador haya seleccionado
- es un ejecutivo?
- es un ejecutivo con moral media?
- es un ejecutivo o tiene moral media?
- es un ejecutivo, dada la información de que el trabajador tiene moral media.
- Dada la información de que el trabajador seleccionado es un ejecutivo, cuál es la probabilidad de que el trabajador
- tiene moral media?
- tiene la moral alta?
- ¿Los siguientes eventos son independientes o dependientes? Explica tu respuesta:
- es un ejecutivo', 'tiene moral media', ¿son estos independientes?
- es un ejecutivo', 'tiene moral alta', ¿son estos independientes?


