1.12: Transformaciones lineales
- Page ID
- 152467
Objetivos de aprendizaje
- Dar la fórmula para una transformación lineal
- Determinar si una transformación es lineal
- Describir lo que es lineal acerca de una transformación lineal
A menudo es necesario transformar los datos de una escala de medición a otra. Por ejemplo, es posible que desee convertir la altura medida en pies a la altura medida en pulgadas. En la tabla se\(\PageIndex{1}\) muestran las alturas de cuatro personas medidas tanto en pies como en pulgadas. Para transformar pies en pulgadas, simplemente multiplicas por\(12\). De igual manera, para transformar pulgadas a pies, se divide por\(12\).
| Pies | Pulgadas |
|---|---|
| 5.00 | 60 |
| 6.25 | 75 |
| 5.50 | 66 |
| 5.75 | 69 |
Algunas conversiones requieren que multipliques por un número y luego agregues un segundo número. Un buen ejemplo de ello es la transformación entre grados Celsius y grados Fahrenheit. \(\PageIndex{2}\)La tabla muestra las temperaturas de cinco ciudades de Estados Unidos a primera hora de la tarde de\(\text{November 16, 2002}\).
| Ciudad | Grados Fahrenheit | Grados Celsius |
|---|---|---|
| Houston | 54 | 12.22 |
| Chicago | 37 | 2.78 |
| Minneapolis | 31 | -0.56 |
| Miami | 78 | 25.56 |
| Phoenix | 70 | 21.11 |
La fórmula para transformar Celsius a Fahrenheit es:
\[F = 1.8C + 32\]
La fórmula para convertir de Fahrenheit a Celsius es
\[C = 0.5556F - 17.778\]
La transformación consiste en multiplicar por una constante y luego agregar una segunda constante. Para la conversión de Celsius a Fahrenheit, la primera constante es\(1.8\) y la segunda es\(32\).
La figura\(\PageIndex{1}\) muestra una gráfica de grados Celsius en función de grados Fahrenheit. Observe que los puntos forman una línea recta. Este siempre será el caso si la transformación de una escala a otra consiste en multiplicar por una constante y luego agregar una segunda constante. Tales transformaciones se denominan, por lo tanto, transformaciones lineales.
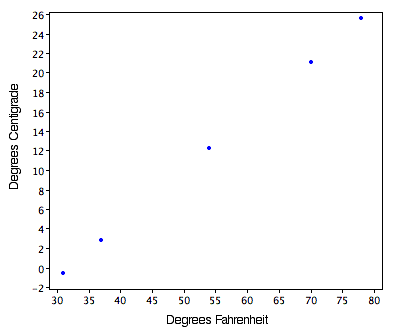
Muchas transformaciones no son lineales. Con transformaciones no lineales, los puntos en una gráfica de la variable transformada contra la variable original no caerían en línea recta. Ejemplos de transformaciones no lineales son: raíz cuadrada, elevación a una potencia, logaritmo y cualquiera de las funciones trigonométricas.
- David M. Lane


