3.5: Simulación de diferencias absolutas
- Page ID
- 152230
Objetivos de aprendizaje
- Aprender qué medida de tendencia central minimiza la suma de las desviaciones absolutas
Instrucciones
Esta demostración le permite examinar la suma de las desviaciones absolutas de un valor dado. La gráfica de la derecha muestra los números\(1, 2, 3, 4,\)\(5\) y sus desviaciones de un valor inicial arbitrario de\(0.254\) (la figura muestra esto redondeado a\(0.25\)).
El primer número,\(1\), está representado por un punto rojo. La desviación de\(0.254\) está representada por una línea roja desde el punto rojo hasta la línea negra. El valor de la línea negra es\(0.254\). De igual manera, el número\(2\) está representado por un punto azul y su desviación de\(0.254\) se representa por la longitud de una línea azul.
La porción de la gráfica con los rectángulos coloreados muestra la suma de las desviaciones absolutas. La suma de las desviaciones es igual a\(0.746 + 1.746 + 2.746 + 3.746 + 4.746 = 13.73\) como se muestra por la altura de la barra coloreada.
En esta demostración, puedes mover la barra negra haciendo clic sobre ella y arrastrándola hacia arriba o hacia abajo. Para ver cómo funciona, muévalo hacia arriba\(1.0\). La desviación del punto rojo de la barra negra es ahora\(0\) ya que ambos son\(1\). La suma de las desviaciones es ahora\(10\).
A medida que mueve la barra hacia arriba y hacia abajo, el valor de la suma de las desviaciones absolutas cambia. Ve si puedes encontrar la colocación de la barra negra que produce el valor más pequeño para la suma de las desviaciones absolutas. Para verificar y ver si encontró el valor más pequeño, haga clic en el botón “Aceptar” en la parte inferior de la gráfica. Se moverá la barra a la ubicación que produce la menor suma de desviaciones absolutas.
También puedes mover los puntos individuales. Da click en uno de los puntos y muévalo hacia arriba o hacia abajo y anota el efecto. Tu objetivo para esta demostración es descubrir una regla para determinar qué valor te dará la menor suma de desviaciones absolutas. Cuando hayas descubierto la regla, regresa y responde de nuevo a las preguntas.
Instrucciones ilustradas
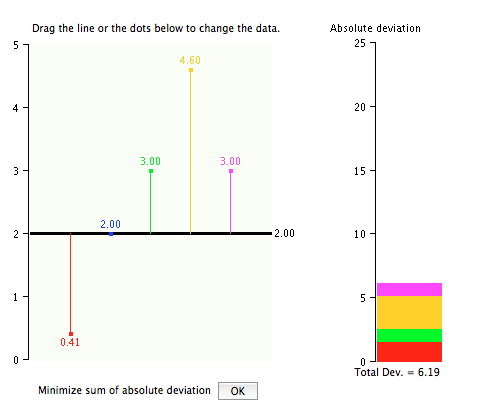
A continuación se muestra una captura de pantalla de la pantalla de inicio del simulatón.
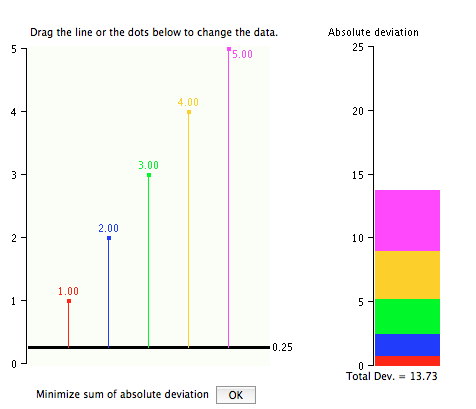
A continuación se muestra un ejemplo después de que se haya cambiado la línea vertical. Se han recalculado las distancias a la línea.
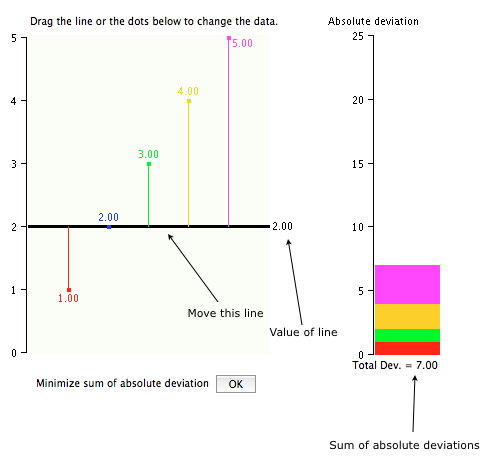
Puede cambiar los datos haciendo clic en un punto de datos y arrastrando. A continuación se muestra un ejemplo con datos modificados.