3.7: Mediana y Media
- Page ID
- 152274
Objetivos de aprendizaje
- Anotar si es la media o mediana la que minimiza la desviación absoluta media
- Anotar si es la media o la mediana que es el punto de equilibrio en una escala de balance
En la sección “Qué es tendencia central”, vimos que el centro de una distribución podría definirse de tres maneras:
- el punto en el que se equilibraría una distribución
- el valor cuya desviación absoluta promedio de todos los demás valores se minimiza
- el valor cuya diferencia cuadrática promedio de todos los demás valores se minimiza
A partir de la simulación de este capítulo, descubriste (esperamos) que la media es el punto en el que se equilibraría una distribución, la mediana es el valor que minimiza la suma de las desviaciones absolutas, y la media es el valor que minimiza la suma de las desviaciones cuadradas.
El cuadro\(\PageIndex{1}\) muestra las desviaciones absolutas y cuadradas de los números\(2, 3, 4, 9\) y\(16\) de su mediana de\(4\) y su media de\(6.8\). Se puede ver que la suma de las desviaciones absolutas de la mediana (\(20\)) es menor que la suma de las desviaciones absolutas de la media (\(22.8\)). Por otro lado, la suma de las desviaciones cuadradas de la mediana (\(174\)) es mayor que la suma de las desviaciones cuadradas de la media (\(134.8\)).
| Valor | Desviación absoluta de la mediana | Desviación absoluta de la media | Desviación cuadrada de la mediana | Desviación cuadrada de la media |
|---|---|---|---|---|
| 2 | 2 | 4.8 | 4 | 23.04 |
| 3 | 1 | 3.8 | 1 | 14.44 |
| 4 | 0 | 2.8 | 0 | 7.84 |
| 9 | 5 | 2.2 | 25 | 4.84 |
| 16 | 12 | 9.2 | 144 | 84.64 |
| Total | 20 | 22.8 | 174 | 134.8 |
La figura\(\PageIndex{1}\) muestra que la distribución se equilibra a la media de\(6.8\) y no a la mediana de\(4\). Las ventajas y desventajas relativas de la media y la mediana se discuten en la sección “Comparando medidas” más adelante en este capítulo.
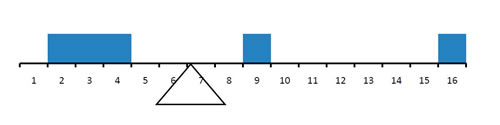
Cuando una distribución es simétrica, entonces la media y la mediana son las mismas. Considera la siguiente distribución:\(1, 3, 4, 5, 6, 7, 9\). La media y la mediana son ambas\(5\). La media, mediana y modo son idénticos en la distribución normal acampanada.


