3.8: Demostración media y mediana
- Page ID
- 152262
Objetivos de aprendizaje
- Estudiar el cambio medio y mediano con diferentes distribuciones
Instrucciones
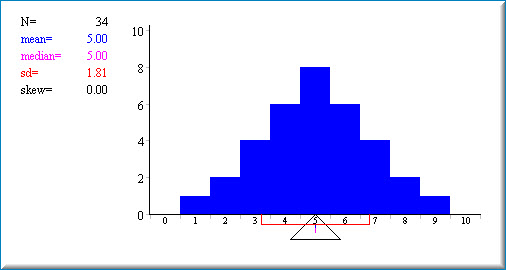
Esta demostración muestra cómo el tamaño relativo de la media y la mediana depende del sesgo de la distribución. La demostración comienza mostrando un histograma de una distribución simétrica (sin sesgo). La media y la mediana son ambas\(5.0\). La media se muestra en el histograma como una pequeña línea azul; la mediana se muestra como una pequeña línea púrpura. La desviación estándar es\(1.81\). Una línea roja extiende una sd en cada dirección desde la media. La desviación estándar se calcula asumiendo que los datos retratados en la gráfica representan a toda la población. Se pueden cambiar los valores del conjunto de datos “pintando” el histograma con el ratón. Cambiar la distribución de varias maneras y anotar cómo el sesgo afecta si la media es mayor que la mediana o viceversa.
Instrucciones ilustradas
La simulación comienza con una distribución simétrica. Como se puede ver en la captura de pantalla de abajo la media y la mediana son iguales y hay\(0\) sesgo.
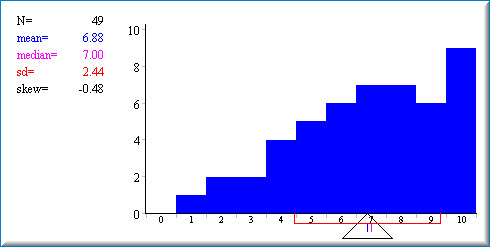
La distribución se puede cambiar “pintándola” con el ratón. A continuación se muestra un ejemplo de una distribución sesgada negativamente. Tenga en cuenta que la media y la mediana ya no son iguales entre sí. Intentar pintar varios tipos diferentes de distribuciones para ver cómo los valores medios y medianos se ven afectados entre sí.