3.15: Formas de Distribuciones
- Page ID
- 152283
Objetivos de aprendizaje
- Compute el sesgo usando dos fórmulas diferentes
- Curtosis computacional
Vimos en la sección sobre distribuciones del Capítulo 1 que las formas de las distribuciones pueden diferir en sesgo y/o curtosis. En esta sección se presentan los índices numéricos de estas dos medidas de forma.
sesgar
La figura\(\PageIndex{1}\) muestra una distribución con un sesgo positivo muy grande. Recordemos que las distribuciones con sesgo positivo tienen colas que se extienden hacia la derecha.
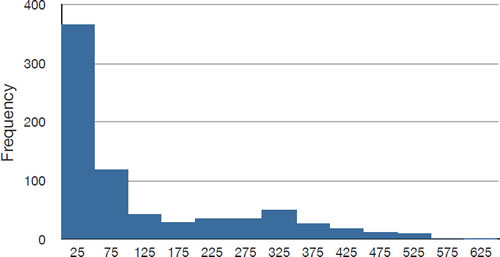
Las distribuciones con sesgo positivo normalmente tienen medias mayores que las medianas. La media y mediana de los salarios de béisbol mostrados en la Figura\(\PageIndex{1}\) son\(\$1,183,417\) y\(\$500,000\) respectivamente. Así, para esta distribución altamente sesgada, la media es más del doble de alta que la mediana. La relación entre el sesgo y el tamaño relativo de la media y mediana llevó al estadístico Pearson a proponer el siguiente índice numérico simple y conveniente de sesgo:
\[\frac{3(Mean-Median)}{\sigma }\]
La desviación estándar de los salarios del beisbol es\(1,390,922\). Por lo tanto, la medida de sesgo de Pearson para esta distribución es\(\dfrac {3(1,183,417 - 500,000)}{1,390,922} = 1.47\).
Así como hay varias medidas de tendencia central, hay más de una medida de sesgo. Aunque la medida de Pearson es buena, la siguiente medida es más utilizada. A veces se le conoce como el tercer momento sobre la media.
\[\sum \dfrac {(X-\mu )^3}{\sigma ^3}\]
Curtosis
La siguiente medida de curtosis es similar a la definición de sesgo. Se resta el valor\(3\) "" para definir “no curtosis” como la curtosis de una distribución normal. De lo contrario, una distribución normal tendría una curtosis de\(3\).
\[\sum \dfrac {(X-\mu )^4}{\sigma ^4}-3\]


