4.2: Valores de la correlación de Pearson
- Page ID
- 152432
Objetivos de aprendizaje
- Describir lo que mide la correlación de Pearson
- Dar los símbolos para la correlación de Pearson en la muestra y en la población
- Indicar el posible rango para la correlación de Pearson
- Identificar una relación lineal perfecta
El coeficiente de correlación producto-momento de Pearson es una medida de la fuerza de la relación lineal entre dos variables. Se le conoce como correlación de Pearson o simplemente como el coeficiente de correlación. Si la relación entre las variables no es lineal, entonces el coeficiente de correlación no representa adecuadamente la fuerza de la relación entre las variables.
El símbolo para la correlación de Pearson es\(ρ\) "" cuando se mide en la población y\(r\) "" cuando se mide en una muestra. Debido a que trataremos casi exclusivamente con muestras, usaremos\(r\) para representar la correlación de Pearson a menos que se indique lo contrario.
Pearson\(r\) puede variar desde\(-1\) hasta\(1\). Una\(r\) de\(-1\) indica una relación lineal negativa perfecta entre variables, una\(r\) de\(0\) indica que no hay relación lineal entre variables y una\(r\) de\(1\) indica una relación lineal positiva perfecta entre variables. La figura\(\PageIndex{1}\) muestra una gráfica de dispersión para la cual\(r = 1\).
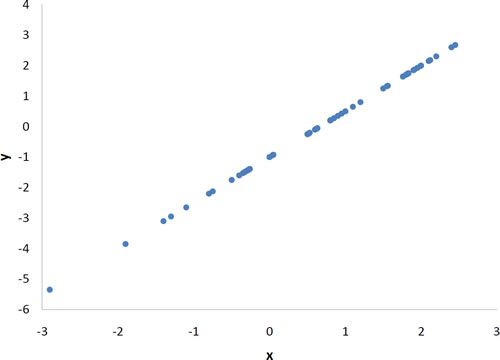
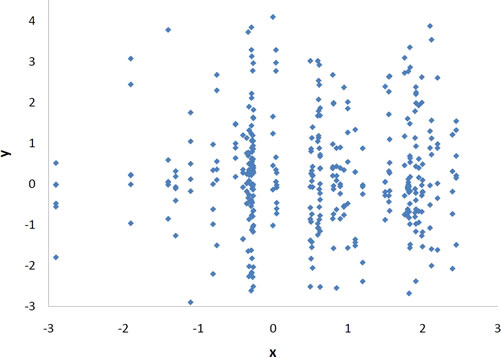
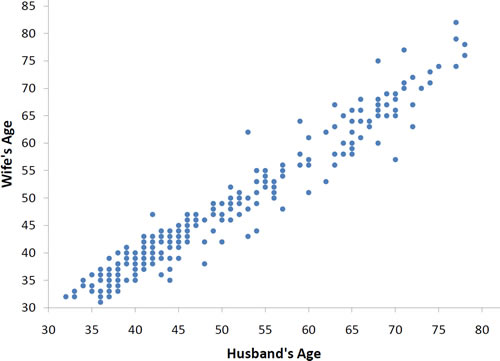
Con datos reales, no esperarías obtener valores\(r\) de exactamente\(-1, 0,\: or\; 1\). Los datos para las edades conyugales mostrados en la Figura\(\PageIndex{4}\) y descritos en la sección introductoria tienen una\(r\) de\(0.97\).
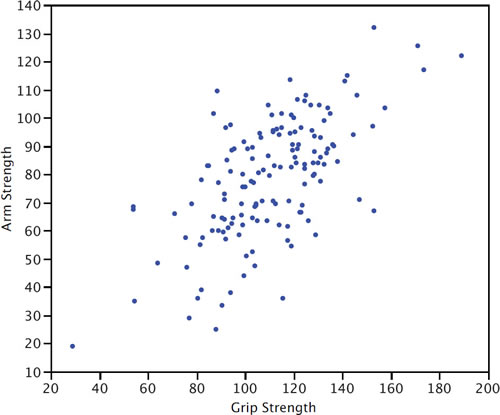
La relación entre la fuerza de agarre y la resistencia del brazo representada en la Figura\(\PageIndex{5}\) (también descrita en la sección introductoria) es\(0.63\).


