8.1: Parcelas Q-Q
- Page ID
- 152146
Objetivos de aprendizaje
- Declarar para qué\(q-q\) parcelas se utilizan.
- Describir la forma de una\(q-q\) parcela cuando se cumple la suposición distribucional.
- Ser capaz de crear una\(q-q\) parcela normal.
El cuantil-cuantil o\(q-q\) gráfica es un dispositivo gráfico exploratorio utilizado para verificar la validez de una suposición distribucional para un conjunto de datos. En general, la idea básica es calcular el valor teóricamente esperado para cada punto de datos en función de la distribución en cuestión. Si los datos siguen efectivamente la distribución asumida, entonces los puntos en la\(q-q\) parcela caerán aproximadamente en línea recta.
Antes de profundizar en los detalles de\(q-q\) las parcelas, primero describimos dos métodos gráficos relacionados para evaluar supuestos distribucionales: el histograma y la función de distribución acumulativa (CDF). Como se verá,\(q-q\) las parcelas son más generales que estas alternativas.
Evaluación de suposiciones distribucionales
Como ejemplo, considere los datos medidos desde un dispositivo físico como el spinner representado en la Figura\(\PageIndex{1}\). La flecha roja gira alrededor del centro, y cuando la flecha deja de girar,\(1\) se registra el número entre\(0\) y. ¿Podemos determinar si el spinner es justo?
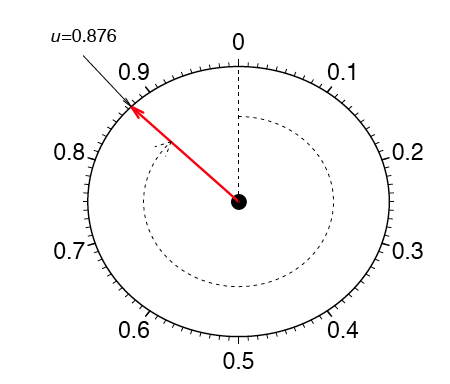
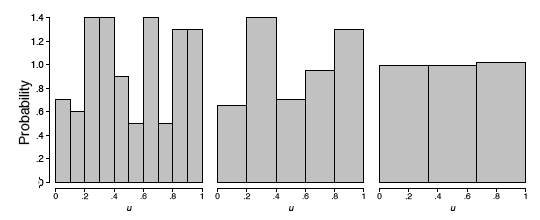
Si el spinner es justo, entonces estos números deben seguir una distribución uniforme. Para investigar si el spinner es justo, gira los\(n\) tiempos de las flechas y registra las medidas por\({\mu _1, \mu _2, ..., \mu _n}\). En este ejemplo, recolectamos\(n = 100\) muestras. El histograma proporciona una visualización útil de estos datos. En la Figura\(\PageIndex{2}\), mostramos tres histogramas diferentes en una escala de probabilidad. El histograma debe ser plano para una muestra uniforme, pero la percepción visual varía dependiendo de si el histograma tiene\(10\)\(5\), o\(3\) bins. El último histograma parece plano, pero los otros dos histogramas no son obviamente planos. No está claro en qué histograma debemos basar nuestra conclusión.
Alternativamente, podríamos usar la función de distribución acumulativa (CDF), que se denota por\(F(\mu )\). El CDF da la probabilidad de que el spinner dé un valor menor o igual a\(\mu\), es decir, la probabilidad de que la flecha roja aterrice en el intervalo\([0, \mu ]\). Por simple aritmética\(F(\mu ) = \mu\),, que es la línea recta diagonal\(y = x\). El CDF basado en los datos de la muestra se llama el CDF empírico (ECDF), se denota por\(\widehat{F}_n(u)\), y se define como la fracción de los datos menor o igual a\(\mu\); es decir,
\[\widehat{F}_n(u)=\frac{\#u_i\leq u}{n}\]
En general, el ECDF adquiere una apariencia de escalera desigual.
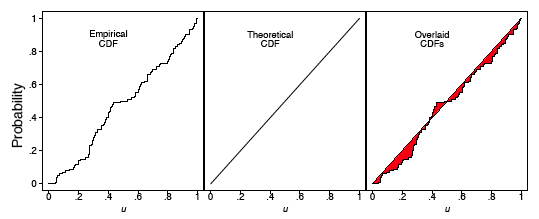
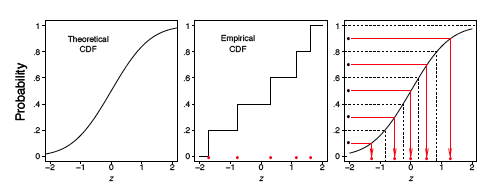
Para la muestra hiladora analizada en la Figura\(\PageIndex{2}\), se computaron los ECDF y CDF, los cuales se muestran en la Figura\(\PageIndex{3}\). En el marco izquierdo, el ECDF aparece cerca de la línea\(y = x\), que se muestra en el marco medio. En el marco derecho, superponemos estas dos curvas y verificamos que de hecho están bastante cerca una de la otra. Observe que no necesitamos especificar el número de bins como ocurre con el histograma.
Gráfica q-q para datos uniformes
La\(q-q\) gráfica para datos uniformes es muy similar al gráfico empírico CDF, excepto con los ejes invertidos. La\(q-q\) gráfica proporciona una comparación visual de los cuantiles de muestra con los cuantiles teóricos correspondientes. En general, si los puntos de una\(q-q\) trama se apartan de una línea recta, entonces se pone en tela de juicio la distribución asumida.
Aquí definimos el cuantil qésimo de un lote de n números como un número\(ξ_q\) tal que una fracción q x n de la muestra es menor que\(ξ_q\), mientras que una fracción\((1 - q) \times n\) de la muestra es mayor que\(ξ_q\). El cuantil más conocido es la mediana\(ξ_{0.5}\), que se localiza en el centro de la muestra.
Considera una pequeña muestra de\(5\) números de la hilandera:
\[\mu _1 = 0.41,\; \mu _2 =0.24,\; \mu _3 =0.59,\; \mu _4 =0.03,\; \mu _5 =0.67\]
Basándonos en nuestra descripción del spinner, esperamos una distribución uniforme para modelar estos datos. Si los datos de la muestra fueran “perfectos”, entonces en promedio habría una observación en medio de cada uno de los\(5\) intervalos:\(0\)\(0.2\) a\(0.2\)\(0.4\),\(0.4\) a\(0.6\), y así sucesivamente. Tabla\(\PageIndex{1}\) muestra los puntos de\(5\) datos (ordenados en orden ascendente) y el valor teóricamente esperado de cada uno basado en el supuesto de que la distribución es uniforme (la mitad del intervalo).
| Datos (μ) | Rango (i) | Medio del i º Intervalo |
|---|---|---|
| 0.03 | 1 | 0.1 |
| 0.24 | 2 | 0.3 |
| 0.41 | 3 | 0.5 |
| 0.59 | 4 | 0.7 |
| 0.67 | 5 | 0.9 |
Las CDF teóricas y empíricas se muestran en la Figura\(\PageIndex{4}\) y la\(q-q\) gráfica se muestra en el marco izquierdo de la Figura\(\PageIndex{5}\).
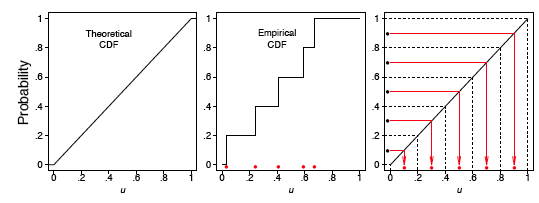
En general, consideramos que el conjunto completo de cuantiles de muestra son los valores de datos ordenados
\[μ_{(1)} < μ_{(2)} < μ_{(3)} < \ldots < μ_{(n-1)} < μ_{(n)} ,\]
donde los paréntesis en el subíndice indican que los datos han sido ordenados. En términos generales, esperamos que el primer valor ordenado esté en la mitad del intervalo\((0, 1/n)\), el segundo esté en la mitad del intervalo\((1/n, 2/n)\) y el último esté en la mitad del intervalo\((\tfrac{n - 1}{n}, 1)\). Así, tomamos como cuantil teórico el valor
\[\xi _q=q\approx \frac{i-0.5}{n}\]
donde\(q\) corresponde al valor de la muestra\(i^{th}\) ordenada. Restamos la cantidad\(0.5\) para que estemos exactamente en la mitad del intervalo\((\tfrac{i-1}{n}, \tfrac{i}{n})\). Estas ideas se representan en el marco derecho de la Figura\(\PageIndex{4}\) para nuestra pequeña muestra de tamaño\(n = 5\).
Ahora estamos preparados para definir la\(q-q\) trama con precisión. Primero, calculamos los n valores esperados de los datos, que emparejamos con los n puntos de datos ordenados en orden ascendente. Para la densidad uniforme, la\(q-q\) parcela está compuesta por los pares\(n\) ordenados
\[(\tfrac{i-0.5}{n}, u_i),\; for\; i=1,2,\cdots ,n\]
Esta definición es ligeramente diferente a la del ECDF, que incluye los puntos\((u_i, \tfrac{i}{n})\). En el marco izquierdo de la Figura\(\PageIndex{5}\), mostramos la\(q-q\) gráfica de los\(5\) puntos en Tabla\(\PageIndex{1}\). En los dos fotogramas de la derecha de la Figura\(\PageIndex{5}\), mostramos la\(q-q\) gráfica del mismo lote de números utilizados en la Figura\(\PageIndex{2}\). En el marco final, agregamos la línea diagonal\(y = x\) como punto de referencia.
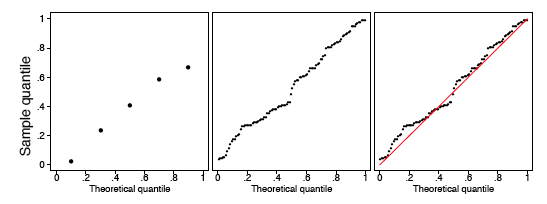
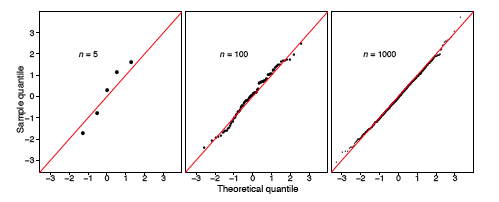
Se debe tener en cuenta el tamaño de la muestra a la hora de juzgar qué tan cerca está la\(q-q\) parcela de la línea recta. Mostramos otras dos muestras uniformes de tamaño\(n = 10\) y\(n = 1000\) en Figura\(\PageIndex{6}\). Observe que la\(q-q\) parcela cuando\(n = 1000\) es casi idéntica a la línea\(y = x\), mientras que tal no es el caso cuando el tamaño de la muestra es solo\(n = 10\).
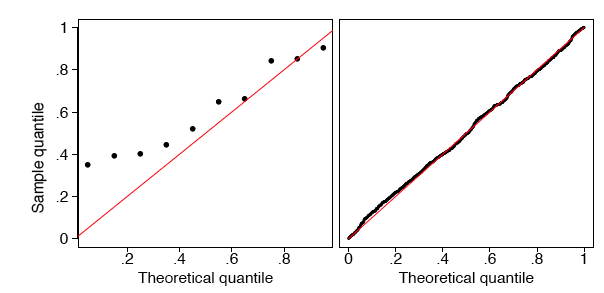
En la Figura\(\PageIndex{7}\), se muestran las\(q-q\) gráficas de dos muestras aleatorias que no son uniformes. En ambos ejemplos, los cuantiles de muestra coinciden con los cuantiles teóricos solo en la mediana y en los extremos. Ambas muestras parecen ser simétricas alrededor de la mediana. Pero los datos en el cuadro izquierdo están más cerca de la mediana de lo que se esperaría si los datos fueran uniformes. Los datos en el marco derecho están más alejados de la mediana de lo que se esperaría si los datos fueran uniformes.
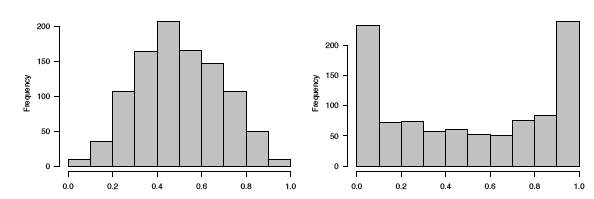
De hecho, los datos se generaron en el\(R\) lenguaje a partir de distribuciones beta con\(a = b = 3\) parámetros a la izquierda y a\(a = b =0.4\) la derecha. En la Figura\(\PageIndex{8}\) mostramos histogramas de estos dos conjuntos de datos, los cuales sirven para aclarar las verdaderas formas de las densidades. Estos son claramente no uniformes.
Gráfica q-q para datos normales
La definición de la\(q-q\) parcela puede extenderse a cualquier densidad continua. La\(q-q\) trama estará cerca de una línea recta si la densidad asumida es correcta. Debido a que la función de distribución acumulativa de la densidad uniforme era una línea recta, la\(q-q\) parcela fue muy fácil de construir. Para datos que no sean uniformes, los cuantiles teóricos deben ser calculados de manera diferente.
Dejar\({z_1, z_2, ..., z_n}\) denotar una muestra aleatoria de una distribución normal con media\(\mu =0\) y desviación estándar\(\sigma =1\). Deje que los valores ordenados sean denotados por
\[z_{(1)} < z_{(2)} < z_{(3)} < \ldots < z_{(n-1)} <z_{(n)}\]
Estos n valores ordenados desempeñarán el papel de los cuantiles de muestra.
Consideremos una muestra de\(5\) valores de una distribución para ver cómo se comparan con lo que se esperaría para una distribución normal. Los\(5\) valores en orden ascendente se muestran en la primera columna de la Tabla\(\PageIndex{2}\).
| Datos (z) | Rango (i) | Medio del i º Intervalo | Normal (z) |
|---|---|---|---|
| -1.96 | 1 | 0.1 | -1.28 |
| -0.78 | 2 | 0.3 | -0.52 |
| 0.31 | 3 | 0.5 | 0.00 |
| 1.15 | 4 | 0.7 | 0.52 |
| 1.62 | 5 | 0.9 | 1.28 |
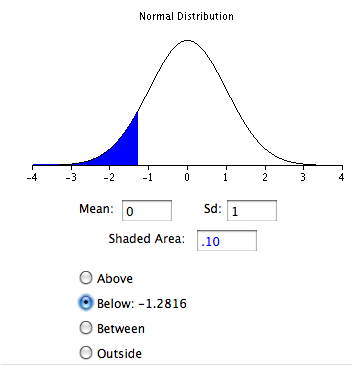
Así como en el caso de la distribución uniforme, tenemos\(5\) intervalos. Sin embargo, con una distribución normal el cuantil teórico no es la mitad del intervalo sino la inversa de la distribución normal para la mitad del intervalo. Tomando como ejemplo el primer intervalo, queremos conocer el\(z\) valor tal que el\(0.1\) del área en la distribución normal está por debajo\(z\). Esto se puede calcular usando la Calculadora Normal Inversa como se muestra en la Figura\(\PageIndex{9}\). Simplemente establezca el campo “Área sombreada” a la mitad del intervalo (\(0.1\)) y haga clic en el botón “Abajo”. El resultado es\(-1.28\). Por lo tanto,\(10\%\) de la distribución está por debajo de un\(z\) valor de\(-1.28\).
La\(q-q\) gráfica para los datos en la Tabla\(\PageIndex{2}\) se muestra en el marco izquierdo de la Figura\(\PageIndex{11}\).
En general, ¿qué debemos tomar como los cuantiles teóricos correspondientes? Dejar que la función de distribución acumulativa de la densidad normal sea denotada por\(\Phi (z)\). En el ejemplo anterior,\(\Phi (-1.28)=0.10\) y\(\Phi (0.00)=0.50\). Usando la notación cuantil, si\(\xi _q\) es el\(q^{th}\) cuantil de una distribución normal, entonces
\[Φ(ξ_q)= q\]
Es decir, la probabilidad de que una muestra normal sea menor de la que en realidad\(\xi _q\) es justa\(q\).
Considerar el primer valor ordenado,\(z_1\). ¿Cuál podríamos esperar que sea el valor de\(\Phi (z_1)\)? Intuitivamente, esperamos que esta probabilidad tome un valor en el intervalo\((0, 1/n)\). De igual manera, esperamos\(\Phi (z_2)\) tomar un valor en el intervalo\((1/n, 2/n)\). Continuando, esperamos\(\Phi (z_n)\) caer en el intervalo\(((n - 1)/n, 1)\). Así, el cuantil teórico que deseamos se define por el inverso (no recíproco) del CDF normal. En particular, el cuantil teórico correspondiente al cuantil empírico\(z_i\) debe ser
\[ξ_q \approx \dfrac{i-0.5}{n}\]
para\(i = 1, 2, \ldots, n\).
La CDF empírica y la construcción teórica del cuantil para la muestra pequeña dada en la Tabla se\(\PageIndex{2}\) muestran en la Figura\(\PageIndex{10}\). Para la muestra más grande de tamaño\(100\), los primeros cuantiles esperados son\(-2.576\),\(-2.170\), y\(-1.960\).
En el marco izquierdo de la Figura\(\PageIndex{11}\), mostramos la\(q-q\) gráfica de la pequeña muestra normal dada en la Tabla\(\PageIndex{2}\). Los fotogramas restantes en la Figura\(\PageIndex{11}\) muestran las\(q-q\) gráficas de muestras aleatorias normales de tamaño\(n = 100\) y\(n = 1000\). A medida que aumenta el tamaño de la muestra, los puntos en las\(q-q\) parcelas se encuentran más cerca de la línea\(y = x\).
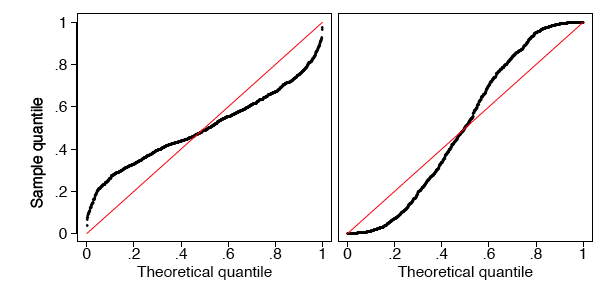
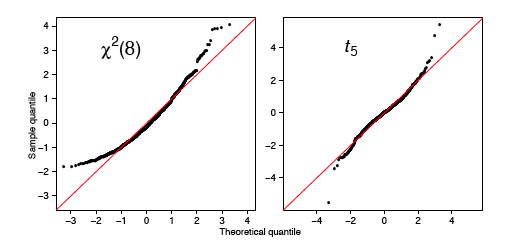
Como antes, una\(q-q\) parcela normal puede indicar desviaciones de la normalidad. Los dos ejemplos más comunes son los datos sesgados y los datos con colas pesadas (curtosis grande). En la Figura\(\PageIndex{12}\), mostramos\(q-q\) gráficas normales para un conjunto de datos chi-cuadrado (sesgado) y un conjunto de datos Student's-\(t\) (kurtóticos), ambos de tamaño\(n = 1000\). Los datos se estandarizaron primero. La línea roja es otra vez\(y = x\). Observe, en particular, que los datos de la\(t\) distribución siguen bastante de cerca la curva normal hasta la última docena de puntos en cada extremo.
gráficas q-q para datos normales con media general y escala
Nuestra discusión previa de\(q-q\) parcelas para datos normales asumió que nuestros datos estaban estandarizados. Un enfoque para construir\(q-q\) parcelas es primero estandarizar los datos y luego proceder como se describió anteriormente. Una alternativa es construir la gráfica directamente a partir de datos brutos.
En esta sección, presentamos un enfoque general para datos que no están estandarizados. ¿Por qué estandarizamos los datos en la Figura\(\PageIndex{12}\)? La\(q-q\) trama se compone de los\(n\) puntos
\[\left ( \Phi ^{-1}\left ( \frac{i-5}{n} \right ),z_i \right )\; for\; i=1,2,...,n\]
Si los datos originales {\(z_i\)} son normales, pero tienen una media arbitraria\(\mu\) y una desviación estándar\(\sigma\), entonces la línea\(y = x\) no coincidirá con los cuantiles teóricos esperados. Claramente, la transformación lineal
\[μ + σ ξ_q\]
proporcionaría el cuantil\(q^{th}\) teórico en la escala transformada. En la práctica, con un nuevo conjunto de datos\(\{x_1,x_2, \ldots, x_n\}\),
la\(q-q\) trama normal consistiría en los n puntos
\[\left ( \Phi ^{-1}\left ( \frac{i-5}{n} \right ),x_i \right )\; for\; i=1,2,...,n\]
En lugar de trazar la línea\(y = x\) como una línea de referencia, la línea
\[y = M + s · x\]
deben estar compuestos, donde\(M\) y\(s\) son los momentos muestrales (media y desviación estándar) correspondientes a los momentos teóricos\(\mu\) y\(\sigma\). Alternativamente, si los datos están estandarizados, entonces la línea\(y = x\) sería apropiada, ya que ahora la media muestral sería\(0\) y la desviación estándar de la muestra sería\(1\).
Ejemplo\(\PageIndex{1}\): SAT Case Study
El estudio de caso del SAT siguió los logros académicos de estudiantes\(105\) universitarios con especialización en informática. La primera variable es su puntaje verbal SAT y la segunda es su promedio de calificaciones (GPA) a nivel universitario. Antes de calcular estadísticas inferenciales usando estas variables, debemos verificar si sus distribuciones son normales. En la Figura\(\PageIndex{13}\), se muestran las\(q-q\) parcelas de las variables verbales SAT y GPA universitario.
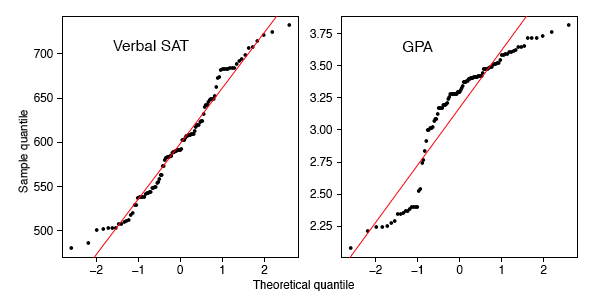
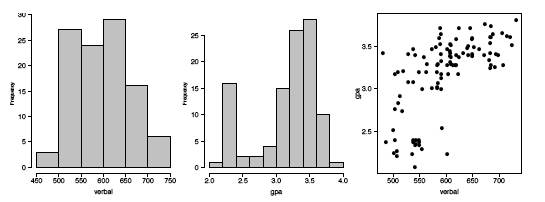
El SAT verbal parece seguir una distribución normal razonablemente bien, excepto en las colas extremas. Sin embargo, la variable GPA universitaria es altamente no normal. Compare la\(q-q\) gráfica GPA con la simulación en el marco derecho de la Figura\(\PageIndex{7}\). Estas cifras son muy similares, a excepción de la región donde\(x\approx -1\). Para seguir estas ideas, calculamos histogramas de las variables y su diagrama de dispersión en la Figura\(\PageIndex{14}\). Estas cifras cuentan una historia bastante diferente. El GPA universitario es bimodal, con aproximadamente\(20\%\) de los estudiantes cayendo en un clúster separado con una calificación de\(C\). El diagrama de dispersión es bastante inusual. Si bien todos los estudiantes de este clúster tienen puntajes SAT verbales por debajo del promedio, hay tantos estudiantes con puntajes SAT bajos cuyos GPA fueron bastante respetables. Podríamos especular sobre la (s) causa (s): diferentes distracciones, diferentes hábitos de estudio, pero solo sería especulación. Pero observe que la correlación cruda entre el SAT verbal y el GPA es bastante alta\(0.65\), pero cuando excluimos el cluster, la correlación para los\(86\) estudiantes restantes cae un poco a\(0.59\).
Discusión
El modelado paramétrico generalmente implica hacer suposiciones sobre la forma de los datos, o la forma de los residuos a partir de un ajuste de regresión. Verificar tales supuestos puede tomar muchas formas, pero una exploración de la forma usando histogramas y\(q-q\) gráficas es muy efectiva. La\(q-q\) gráfica no tiene ningún parámetro de diseño como el número de bins para un histograma.
En un tratamiento avanzado, la\(q-q\) gráfica puede ser utilizada para probar formalmente la hipótesis nula de que los datos son normales. Esto se hace calculando el coeficiente de correlación de los\(n\) puntos en la\(q-q\) parcela. Dependiendo de\(n\), la hipótesis nula es rechazada si el coeficiente de correlación es menor que un umbral. El umbral ya está bastante cerca\(0.95\) para tamaños de muestra modestos.
Hemos visto que la\(q-q\) gráfica para datos uniformes está muy estrechamente relacionada con la función empírica de distribución acumulativa. Para las funciones de densidad general, la llamada transformada integral de probabilidad toma una variable aleatoria\(X\) y la mapea al intervalo (\(0, 1\)) a través de la CDF de\(X\) sí misma, es decir,
\[Y = F_X(X)\]
que se ha demostrado que es una densidad uniforme. Esto explica por qué la\(q-q\) gráfica sobre datos estandarizados siempre está cerca de la línea\(y = x\) cuando el modelo es correcto.
Por último, los científicos han utilizado papel cuadriculado especial durante años para hacer que las relaciones sean lineales (líneas rectas). El ejemplo más común solía ser el papel semi-log, en el que los puntos que siguen la fórmula\(y=ae^{bx}\) aparecen lineales. Esto sigue por supuesto ya que\(log(y) = log(a) + bx\), que es la ecuación para una línea recta. Las\(q-q\) gráficas pueden considerarse como “papel cuadriculado de probabilidad” que hace una gráfica de los valores de datos ordenados en una línea recta. Cada densidad tiene su propio papel cuadriculado de probabilidad especial.


