Saltar al contenido principal
LibreTexts Español

11.E: Lógica de las Pruebas de Hipótesis (Ejercicios)

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    152378

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Es posible que desee utilizar la Calculadora Binomial para algunos de estos ejercicios.

    Preguntas Generales

    Q1

    Se realiza un experimento para probar la afirmación de que James Bond puede saborear la diferencia entre un Martini que se agita y uno que se agita. ¿Cuál es la hipótesis nula? (sección pertinente)

    Q2

    La siguiente explicación es incorrecta. ¿Qué tres palabras deben agregarse para que sea correcta? (sección pertinente)

    El valor de probabilidad es la probabilidad de obtener un estadístico tan diferente del parámetro especificado en la hipótesis nula como el estadístico obtenido en el experimento. El valor de probabilidad se calcula asumiendo que la hipótesis nula es verdadera.

    Q3

    ¿Por qué los experimentadores prueban hipótesis que creen que son falsas? (sección pertinente)

    Q4

    Exponer la hipótesis nula para:

    1. Un experimento que prueba si la equinácea disminuye la duración de los resfriados.
    2. Un estudio correlacional sobre la relación entre el tamaño del cerebro y la inteligencia.
    3. Una investigación sobre si un psíquico autoproclamado puede predecir el resultado de un volteo de moneda.
    4. Un estudio que compara un medicamento con un placebo sobre la cantidad de alivio del dolor. (Se utilizó una prueba de una cola).
      (sección relevante y sección relevante)

    Q5

    Supongamos que la hipótesis nula es esa\(\mu =50\) y que la gráfica que se muestra a continuación es la distribución muestral de la media (\(M\)). ¿Un valor muestral de\(M= 60\) ser significativo en una prueba de dos colas a\(0.05\) nivel? Aproximadamente, ¿qué valor de se\(M\) necesitaría para ser significativo? (sección relevante y sección relevante)

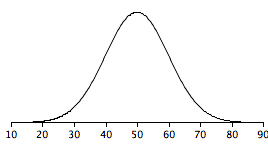
    area_q.gif

    Q6

    Un investigador desarrolla una nueva teoría que predice que los vegetarianos tendrán más de una vitamina particular en su sangre que los no vegetarianos. Se realiza un experimento y los vegetarianos sí tienen más de la vitamina, pero la diferencia no es significativa. El valor de probabilidad es\(0.13\). ¿Debería la confianza del experimentador en la teoría aumentar, disminuir o permanecer igual? (sección pertinente)

    Q7

    Un investigador plantea la hipótesis de que la disminución del colesterol asociada a la pérdida de peso se debe realmente al ejercicio. Para probar esto, el investigador controla cuidadosamente para hacer ejercicio al tiempo que compara los niveles de colesterol de un grupo de sujetos que pierden peso haciendo dieta con un grupo control que no hace dieta. La diferencia entre grupos en colesterol no es significativa. ¿Puede el investigador afirmar que la pérdida de peso no tiene ningún efecto? (sección pertinente)

    Q8

    Se realiza una prueba de significancia y\(p = 0.20\). ¿Por qué el experimentador no puede afirmar que la probabilidad de que la hipótesis nula sea verdadera es\(0.20\)? (sección relevante, sección relevante y sección relevante)

    Q9

    Para que un medicamento sea aprobado por la FDA, se debe demostrar que el medicamento es seguro y efectivo. Si el medicamento es significativamente más efectivo que un placebo, entonces el medicamento se considera efectivo. ¿Qué sabe de la efectividad de un medicamento una vez que ha sido aprobado por la FDA (asumiendo que no ha habido un error de Tipo I)? (sección pertinente)

    Q10

    ¿Cuándo es válido usar una prueba de una cola? ¿Cuál es la ventaja de una prueba de una cola? Dé un ejemplo de una hipótesis nula que sería probada por una prueba de una cola. (sección pertinente)

    Q11

    Distinguir entre valor de probabilidad y nivel de significancia. (sección pertinente)

    Q12

    Supongamos que se realizó un estudio sobre la efectividad de una clase sobre “Cómo tomar pruebas”. Se compararon los puntajes SAT de un grupo experimental y un grupo control. (Había\(100\) sujetos en cada grupo.) La puntuación media del grupo experimental fue\(503\) y la puntuación media del grupo control fue\(499\). Se encontró que la diferencia entre medias fue significativa,\(p = 0.037\). ¿Qué concluye sobre la efectividad de la clase? (sección relevante y sección relevante)

    Q13

    ¿Es más conservador usar un nivel alfa\(0.01\) o un nivel alfa de\(0.05\)? ¿Beta sería mayor para un alfa de\(0.05\) o para un alfa de\(0.01\)? (sección pertinente)

    Q14

    ¿Por qué\(H_o: M_1 = M_2\) no es una hipótesis nula propiamente dicha? (sección pertinente)

    Q15

    Un experimentador espera que un efecto salga en cierta dirección. ¿Es esta base suficiente para usar una prueba de una cola? ¿Por qué o por qué no? (sección pertinente)

    Q16

    ¿En qué se diferencian las tasas de error Tipo I y Tipo II de las pruebas de una cola y de dos colas? (sección relevante y sección relevante)

    Q17

    Una probabilidad de dos colas es\(0.03\). ¿Cuál es la probabilidad de una cola si el efecto estuviera en la dirección especificada? ¿Qué sería si el efecto estuviera en la otra dirección? (sección pertinente)

    Q18

    Usted elige un nivel alfa de\(0.01\) y luego analiza sus datos.

    1. ¿Cuál es la probabilidad de que cometas un error de Tipo I dado que la hipótesis nula es verdadera?
    2. ¿Cuál es la probabilidad de que cometas un error Tipo I dado que la hipótesis nula es falsa? (sección pertinente)

    Q19

    ¿Por qué no tiene sentido probar la hipótesis de que es la media de la muestra\(42\)? (sección relevante y sección relevante)

    Q20

    Verdadero/falso: Es más fácil rechazar la hipótesis nula si el investigador utiliza un nivel alfa (\(\alpha\)) más pequeño. (sección relevante y sección relevante)

    Q21

    Verdadero/falso: Es más probable que cometas un error de Tipo I al usar una muestra pequeña que cuando se usa una muestra grande. (sección pertinente)

    Q22

    Verdadero/falso: Aceptas la hipótesis alternativa cuando rechazas la hipótesis nula. (sección pertinente)

    Q23

    Verdadero/falso: No aceptas la hipótesis nula cuando no la rechazas. (sección pertinente)

    Q24

    Verdadero/falso: Un investigador corre el riesgo de cometer un error Tipo I cada vez que se rechaza la hipótesis nula. (sección pertinente)

    This page titled 11.E: Lógica de las Pruebas de Hipótesis (Ejercicios) is shared under a Public Domain license and was authored, remixed, and/or curated by David Lane via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.