13.5: Factores que afectan el poder
- Page ID
- 152399
Objetivos de aprendizaje
- Indicar cuál es el efecto de cada uno de los factores
Varios factores afectan el poder de una prueba estadística. Algunos de los factores están bajo el control del experimentador, mientras que otros no. El siguiente ejemplo se utilizará para ilustrar los diversos factores.
Supongamos que se sabe que una prueba de logro matemático se distribuye normalmente con una media de\(75\) y una desviación estándar de\(\sigma\). Un investigador está interesado en saber si un nuevo método de enseñanza da como resultado una media superior. Supongamos que aunque el experimentador no lo conozca, la media poblacional\(\mu\) para el nuevo método es mayor que\(75\). El investigador planea muestrear\(N\) sujetos y hacer una prueba de una cola de si la media de la muestra es significativamente mayor que\(75\). En esta sección, consideramos factores que afectan la probabilidad de que el investigador rechace correctamente la falsa hipótesis nula de que la media poblacional es\(75\) o menor. En otras palabras, factores que afectan el poder.
Tamaño de la muestra
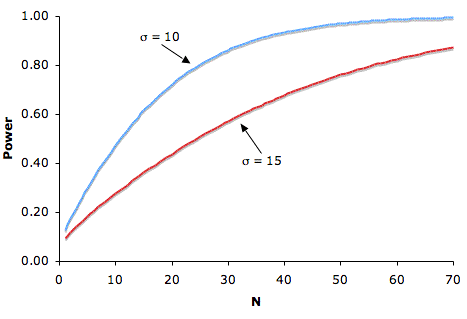
La figura\(\PageIndex{1}\) muestra que cuanto mayor es el tamaño de la muestra, mayor es la potencia. Dado que el tamaño de la muestra suele estar bajo el control de un experimentador, aumentar el tamaño de la muestra es una forma de aumentar la potencia. Sin embargo, a veces es difícil y/o costoso usar un tamaño de muestra grande.
Desviación estándar
La figura\(\PageIndex{1}\) también muestra que la potencia es mayor cuando la desviación estándar es pequeña que cuando es grande. Para todos los valores de\(N\), la potencia es mayor para la desviación estándar de\(10\) que para la desviación estándar de\(15\) (excepto, por supuesto, cuando\(N = 0\)). Los experimentadores a veces pueden controlar la desviación estándar mediante el muestreo de una población homogénea de sujetos, reduciendo el error de medición aleatorio y/o asegurando que los procedimientos experimentales se apliquen de manera muy consistente.
Diferencia entre la media hipotética y la verdadera
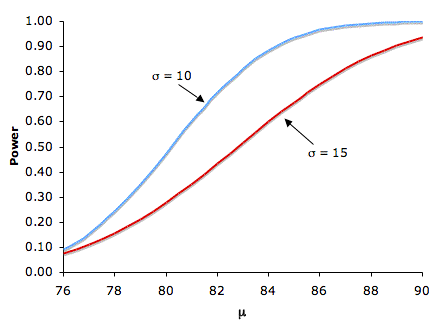
Naturalmente, cuanto mayor sea el tamaño del efecto, más probable es que un experimento encuentre un efecto significativo. La figura\(\PageIndex{2}\) muestra el efecto de aumentar la diferencia entre la media especificada por la hipótesis nula (\(75\)) y la media poblacional\(\mu\) para las desviaciones estándar de\(10\) y\(15\).
Nivel de significancia
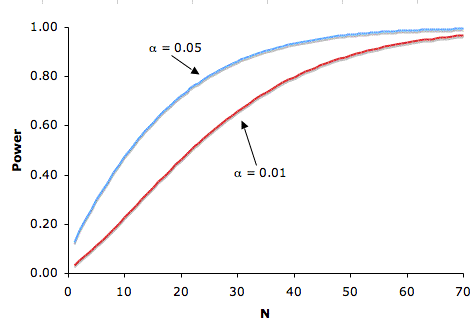
Existe una compensación entre el nivel de significancia y el poder: cuanto más estricto (menor) es el nivel de significancia, menor es el poder. La figura\(\PageIndex{3}\) muestra que la potencia es menor para el\(0.01\) nivel que para el\(0.05\) nivel. Naturalmente, cuanto más fuerte sea la evidencia necesaria para rechazar la hipótesis nula, menor será la probabilidad de que la hipótesis nula sea rechazada.
Pruebas de una o dos colas
La potencia es mayor con una prueba de una cola que con una prueba de dos colas siempre que la dirección hipotética sea correcta. Una prueba de una cola en el\(0.05\) nivel tiene la misma potencia que una prueba de dos colas en el\(0.10\) nivel. Una prueba de una cola, en efecto, eleva el nivel de significancia.


