14.7: Regresión hacia la media
- Page ID
- 152342
Objetivos de aprendizaje
- Estudiar Regresión hacia la media
La regresión hacia la media implica resultados que se deben al menos en parte al azar. Comenzamos con un ejemplo de una tarea que es completamente casualidad: Imagínese un experimento en el que un grupo de\(25\) personas predijo cada uno los resultados de volteretas de una moneda justa. Para cada sujeto del experimento, una moneda es volteada\(12\) veces y el sujeto predice el resultado de cada volteo. La figura\(\PageIndex{1}\) muestra los resultados de una simulación de este “experimento”. Aunque la mayoría de los sujetos fueron correctos de\(5\) a\(8\) tiempos fuera de\(12\), un sujeto simulado fue\(10\) tiempos correctos. Claramente, este tema tuvo mucha suerte y probablemente no le iría tan bien si realizara la tarea por segunda vez. De hecho, la mejor predicción del número de veces que este sujeto sería correcto en la nueva prueba es\(6\), ya que la probabilidad de ser correcto en un juicio dado es\(0.5\) y hay\(12\) juicios.
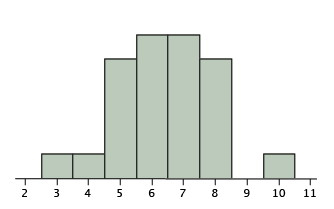
Más técnicamente, la mejor predicción para el resultado del sujeto en la nueva prueba es la media de la distribución binomial con\(N = 12\) y\(p = 0.50\). Esta distribución se muestra en la Figura\(\PageIndex{2}\) y tiene una media de\(6\).
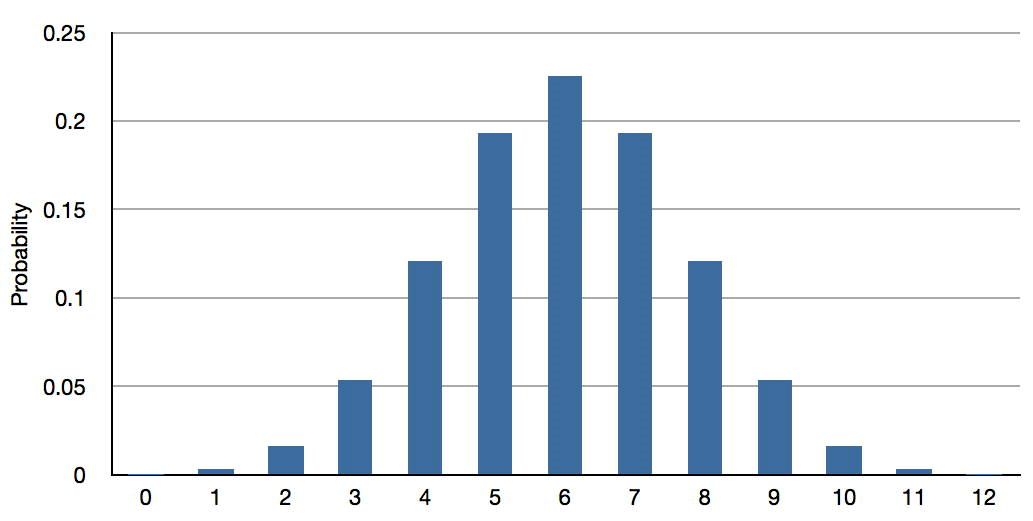
El punto aquí es que no importa cuántos volteos de moneda un sujeto predijo correctamente, la mejor predicción de su puntaje en una nueva prueba es\(6\).
Ahora consideramos una prueba que llamaremos "Prueba A" que es en parte casualidad y en parte habilidad: En lugar de predecir los resultados de los volteos de\(12\) monedas, cada sujeto predice los resultados de los volteos de\(6\) monedas y responde preguntas\(6\) verdaderas/falsas sobre la historia mundial. Supongamos que la puntuación media en las preguntas de\(6\) historia es\(4\). La puntuación de un sujeto en la Prueba A tiene un gran componente de probabilidad pero también depende del conocimiento de la historia. Si un sujeto obtuvo una puntuación muy alta en esta prueba (como una puntuación de\(10/12\)), es probable que le haya ido bien tanto en las preguntas de historia como en los volteos de monedas. Si a este sujeto se le da entonces una segunda prueba (Prueba B) que también incluyera predicciones de monedas y preguntas de historia, su conocimiento de la historia sería útil y nuevamente se esperaría que marcaran por encima de la media. Sin embargo, dado que su alto rendimiento en la porción de monedas de la Prueba A no sería predictivo del desempeño de su moneda en la Prueba B, no se esperaría que les fuera tan bien en la Prueba B como en la Prueba A. Por lo tanto, la mejor predicción de su puntaje en la Prueba B estaría en algún lugar entre su puntaje en la Prueba A y la media de la Prueba B. Esta tendencia de sujetos con valores altos en una medida que incluye oportunidad y habilidad para puntuar más cerca de la media en una nueva prueba se llama "”\(\textit{regression toward the mean}\).
La esencia del fenómeno de la regresión hacia la media es que las personas con puntuaciones altas tienden a estar por encima de la media en habilidad y suerte y que solo la porción de habilidad es relevante para el desempeño futuro. De igual manera, las personas con puntuaciones bajas tienden a estar por debajo del promedio en habilidad y suerte, y su mala suerte no es relevante para el desempeño futuro. Esto no quiere decir que todas las personas que puntúan alto tengan suerte por encima de la media. No obstante, en promedio lo hacen.
Casi todas las medidas de comportamiento tienen una oportunidad y un componente de habilidad para ello. Toma como ejemplo la calificación de un estudiante en un examen final. Ciertamente, el conocimiento del alumno sobre la materia será un determinante mayor de su calificación. Sin embargo, hay aspectos del desempeño que se deben al azar. El examen no puede cubrir todo en el curso y por lo tanto debe representar un subconjunto del material. A lo mejor el alumno tuvo suerte en que el único aspecto del curso que el alumno no entendió bien no estaba bien representado en la prueba. O, tal vez el alumno no estaba seguro cuál de los dos enfoques de un problema sería mejor pero, más o menos por casualidad, eligió el correcto. También entran en juego otros elementos de azar. Quizás el alumno se despertó temprano en la mañana por una llamada telefónica aleatoria, resultando en fatiga y menor rendimiento. Y, por supuesto, adivinar preguntas de opción múltiple es otra fuente de aleatoriedad en los puntajes de las pruebas.
Habrá regresión hacia la media en una situación test-retest siempre que haya menos de una relación perfecta (\(r = 1\)) entre la prueba y la nueva prueba. Esto se desprende de la fórmula para una línea de regresión con variables estandarizadas que se muestran a continuación:
\[Z_{Y'} = (r)(Z_X)\]
A partir de esta ecuación queda claro que si el valor absoluto de\(r\) es menor que\(1\), entonces el valor predicho de\(Z_Y\) estará más cerca de\(0\), la media para las puntuaciones estandarizadas, que es\(Z_X\). También, tenga en cuenta que si la correlación entre\(X\) y\(Y\) es\(0\), como lo sería para una tarea que es toda suerte, la puntuación estándar prevista para\(Y\) es su media,\(0\), independientemente de la puntuación en\(X\).
La figura\(\PageIndex{3}\) muestra una gráfica de dispersión con la línea de regresión que predice el SAT Verbal estandarizado a partir del SAT matemático estandarizado. Obsérvese que la pendiente de la línea es igual a la correlación de\(0.835\) entre estas variables.
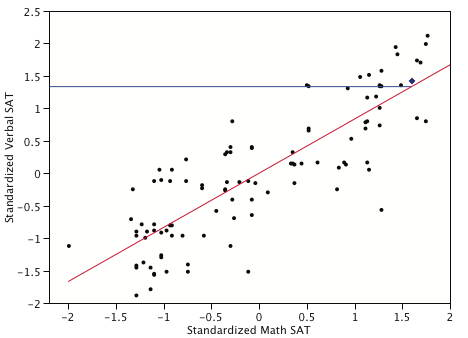
El punto representado por un diamante azul tiene un valor de\(1.6\) en el SAT matemático estandarizado. Esto significa que este estudiante obtuvo desviaciones\(1.6\) estándar por encima de la media en Matemáticas SAT. El puntaje previsto es\((r)(1.6) = (0.835)(1.6) = 1.34\). La línea horizontal en la gráfica muestra el valor de la puntuación predicha. El punto clave es que aunque este estudiante calificó desviaciones\(1.6\) estándar por encima de la media en el SAT de Matemáticas, solo se prevé que puntúe desviaciones\(1.34\) estándar por encima de la media en el SAT Verbal. Así, la predicción es que el puntaje Verbal SAT estará más cerca de la media de\(0\) que el puntaje SAT de Matemáticas. De igual manera, se pronosticará que un estudiante que puntúe muy por debajo de la media en el SAT de Matemáticas obtendrá una puntuación más alta
La regresión hacia la media ocurre en cualquier situación en la que las observaciones se seleccionan sobre la base del desempeño en una tarea que tiene un componente aleatorio. Si eliges a las personas en función de su desempeño en tal tarea, elegirás a las personas en parte en función de su habilidad y en parte en función de su suerte en la tarea. Dado que no se puede esperar que su suerte se mantenga de juicio en juicio, la mejor predicción del desempeño de una persona en un segundo juicio será en algún lugar entre su desempeño en el primer juicio y el rendimiento medio en el primer juicio. El grado en que se espera que el puntaje “retroceda hacia la media” de esta manera depende de las contribuciones relativas del azar y la habilidad a la tarea: cuanto mayor sea el papel del azar, mayor será la regresión hacia la media.
Errores resultantes de la falta de comprensión de la regresión hacia la media
No apreciar la regresión hacia la media es común y a menudo conduce a interpretaciones y conclusiones incorrectas. Uno de los mejores ejemplos es proporcionado por el Premio Nobel Daniel Kahneman en su autobiografía. El doctor Kahneman intentaba enseñar a los instructores de vuelo que la alabanza es más efectiva que el castigo. Fue desafiado por uno de los instructores que retransmitió que en su experiencia alabar a un cadete por ejecutar una maniobra limpia suele ir seguido de un desempeño menor, mientras que gritar a un cadete por mala ejecución suele ir seguido de un mejor desempeño. Esto, por supuesto, es exactamente lo que se esperaría con base en la regresión hacia la media. El rendimiento de un piloto, aunque basado en una habilidad considerable, variará aleatoriamente de una maniobra a otra. Cuando un piloto ejecuta una maniobra extremadamente limpia, es probable que haya tenido un poco de suerte a su favor además de su considerable habilidad. Después de los elogios pero no por ello, el componente suerte probablemente desaparecerá y el rendimiento será menor. De igual manera, es probable que un desempeño deficiente se deba en parte a la mala suerte. Después de las críticas pero no por ello, la próxima actuación probablemente será mejor. Para conducir este punto a casa, Kahneman hizo que cada instructor realizara una tarea en la que se arrojaba una moneda a un blanco dos veces. Demostró que el desempeño de quienes habían hecho lo mejor la primera vez se deterioró, mientras que el desempeño de quienes habían hecho lo peor mejoró.
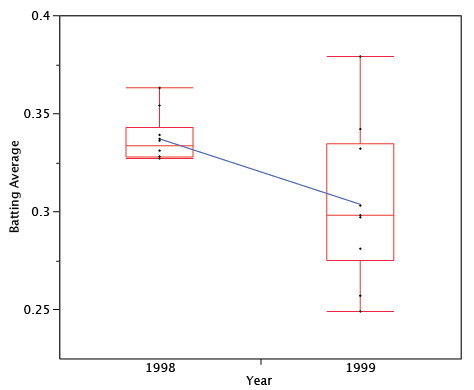
La regresión hacia la media está frecuentemente presente en el rendimiento deportivo. Un buen ejemplo lo proporcionan Schall y Smith (\(2000\)), quienes analizaron muchos aspectos de las estadísticas de béisbol incluyendo los promedios de bateo de los jugadores en\(1998\). Eligieron a los\(10\) jugadores con los promedios de bateo más altos (BA) en\(1998\) y verificaron para ver qué tan bien les fue en\(1999\). De acuerdo con lo que se esperaría con base en la regresión hacia la media, estos jugadores deberían, en promedio, tener promedios de bateo\(1999\) más bajos en que lo hicieron en\(1998\). Como se puede apreciar en la Tabla\(\PageIndex{1}\),\(7/10\) de los jugadores tuvieron promedios de bateo\(1999\) más bajos en que en\(1998\). Además, los que tuvieron promedios más altos en solo\(1999\) fueron ligeramente superiores, mientras que los que fueron más bajos fueron mucho menores. La disminución promedio de\(1998\) a\(1999\) fue\(33\) puntos. Aun así, la mayoría de estos jugadores tuvieron excelentes promedios de bateo al\(1999\) indicar que la habilidad era un componente importante de sus\(1998\) promedios.
| 1998 | 1999 | Diferencia |
|---|---|---|
| 363 | 379 | 16 |
| 354 | 298 | -56 |
| 339 | 342 | 3 |
| 337 | 281 | -56 |
| 336 | 249 | -87 |
| 331 | 298 | -33 |
| 328 | 297 | -31 |
| 328 | 303 | -25 |
| 327 | 257 | -70 |
| 327 | 332 | 5 |
La figura\(\PageIndex{4}\) muestra los promedios de bateo de los dos años. El declive de\(1998\) a\(1999\) es claro. Tenga en cuenta que aunque la media disminuyó de\(1998\), algunos jugadores aumentaron sus promedios de bateo. Esto ilustra que la regresión hacia la media no ocurre para cada individuo. Si bien los puntajes previstos para cada individuo serán menores, algunas de las predicciones serán erróneas.
La regresión hacia la media juega un papel en la llamada “Slump de segundo año”, un buen ejemplo de lo cual es que un jugador que gana “novato del año” normalmente le va menos bien en su segunda temporada. Un fenómeno relacionado se llama el Sports Illustrated Cover Jinx.
Un experimento sin grupo control puede confundir los efectos de regresión con efectos reales. Por ejemplo, considere un experimento hipotético para evaluar un programa de mejora de lectura. Todos los estudiantes de primer grado de un distrito escolar recibieron una prueba de rendimiento de lectura y los\(50\) lectores con menor puntaje se inscribieron en el programa. Los estudiantes fueron reevaluados siguiendo el programa y la mejora media fue grande. ¿Significa esto necesariamente que el programa fue efectivo? No, podría ser que el bajo desempeño inicial de los alumnos se debió, en parte, a la mala suerte. Se esperaría que su suerte mejorara en la nueva prueba, lo que aumentaría sus puntajes con o sin el programa de tratamiento.
Para un ejemplo real, considere un experimento que buscó determinar si el medicamento propranolol aumentaría los puntajes SAT de los estudiantes que se cree que tienen ansiedad ante las pruebas. Se le dio propranolol a los estudiantes de\(25\) preparatoria elegidos debido a que las pruebas de coeficiente intelectual y otros resultados académicos indicaron que no les había ido tan bien como se esperaba en el SAT. En una nueva prueba tomada después de recibir propranolol, los estudiantes mejoraron sus puntajes del SAT en promedio de\(120\) puntos. Esto fue un incremento significativamente mayor que los\(38\) puntos esperados simplemente por haber realizado la prueba antes. El problema con el estudio es que el método de selección de estudiantes probablemente resultó en un número desproporcionado de estudiantes que tuvieron mala suerte cuando tomaron el SAT por primera vez. En consecuencia, estos estudiantes probablemente habrían aumentado sus puntajes en una nueva prueba con o sin el propranolol. Esto no quiere decir que el propranolol no tuvo ningún efecto. Sin embargo, dado que los posibles efectos del propranolol y los efectos de regresión fueron confundidos, no se deben sacar conclusiones firmes.
La asignación aleatoria de estudiantes al grupo de propranolol o a un grupo control habría mejorado el diseño experimental. Dado que los efectos de regresión entonces no habrían sido sistemáticamente diferentes para los dos grupos, una diferencia significativa habría proporcionado buena evidencia de un efecto de propranolol.
Artículo del New York Times sobre el estudio
Schall, T., & Smith, G. (2000) ¿Los beisbolistas retroceden hacia la media? El estadístico americano, 54, 231-235.


