15.E: Análisis de varianza (Ejercicios)
- Page ID
- 152317
Preguntas Generales
Q1
¿Cuál es la hipótesis nula probada por análisis de varianza?
Q2
¿Cuáles son los supuestos del análisis de varianza entre sujetos?
Q3
¿Qué es una variable entre sujetos?
Q4
¿Por qué no solo calcular\(t\) -pruebas entre todos los pares de medias en lugar de calcular un análisis de varianza?
Q5
¿Cuál es la diferencia entre "\(N\)" y "\(n\)“?
Q6
¿Cómo es que las estimaciones de varianza se pueden utilizar para probar una hipótesis sobre las medias?
Q7
Explicar por qué la varianza de las medias muestrales tiene que ser multiplicada por "\(n\)" en el cómputo de\(MSB\).
Q8
¿Qué tipo de sesgo tiene la\(F\) distribución?
Q9
¿Cuándo hacer\(MSB\) y\(MSE\) estimar la misma cantidad?
Q10
Si se realiza un experimento con\(6\) condiciones y\(5\) sujetos en cada condición, ¿qué son\(dfn\) y\(dfe\)?
Q11
¿Cómo se ve afectada la forma de la\(F\) distribución por los grados de libertad?
Q12
¿Cuáles son los dos componentes de la suma total de cuadrados en un diseño de un factor entre sujetos?
Q13
¿Cómo se calcula el cuadrado medio a partir de la suma de cuadrados?
Q14
Un experimentador está interesado en los efectos de dos variables independientes sobre la autoestima. ¿Qué es mejor de realizar un experimento factorial que de realizar dos experiencias separadas, una por cada variable independiente?
Q15
Se realizó un experimento sobre el efecto de la edad y la condición de tratamiento (experimental versus control) sobre la velocidad de lectura. Qué término estadístico (efecto principal, efecto simple, interacción, comparación específica) aplica a cada una de las descripciones de efectos.
- El efecto del tratamiento fue mayor para los niños\(15\) de un año que para los\(5\) niños\(10\) de un año.
- En general, los sujetos en la condición de tratamiento se desempeñaron más rápido que los sujetos en la condición control.
- La diferencia entre los niños de\(10\) - y\(15\) -años fue significativa bajo la condición de tratamiento.
- La diferencia entre los\(15\) niños de un año y el promedio de los niños de\(5\) - y\(10\) -años fue significativa.
- A medida que crecen, los niños leen más rápido.
Q16
Se analiza un diseño\(A(3) \times B(4)\) factorial con\(6\) sujetos en cada grupo. Dar las columnas fuente y grados de libertad de la tabla de resumen de análisis de varianza.
Q17
Los siguientes datos provienen de un estudio hipotético sobre los efectos de la edad y el tiempo en las puntuaciones en una prueba de comprensión lectora. Computar la tabla de resumen de análisis de varianza.
| 12 años | 16 años | |
| 30 minutos | 66 68 59 72 46 |
74 71 67 82 76 |
| 60 minutos | 69 61 69 73 61 |
95 92 95 98 94 |
Q18
Definir “Interacción de tres vías”
Q19
Definir la interacción en términos de efectos simples.
Q20
Trazar una interacción para un\(A(2) \times B(2)\) diseño en el que el efecto de\(B\) es\(A1\) mayor at que en\(A2\). La variable dependiente es “Número correcto”. Asegúrese de etiquetar ambos ejes.
Q21
A continuación se presentan dos gráficas de medias poblacionales para\(2 \times 3\) diseños. Para cada gráfica, indique qué efecto (s) (\(A\),\(B\), o\(A \times B\)) son distintos de cero.
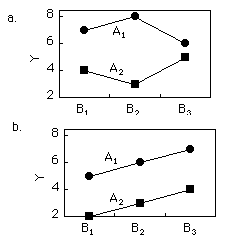
Q22
Los siguientes datos provienen de un diseño\(A(2) \times B(4)\) factorial.
| B1 | B2 | B3 | B4 | |
| A1 | 1 3 4 5 |
2 2 4 5 |
3 4 2 6 |
4 |
| A2 | 1 1 2 |
2 3 2 4 |
4 6 7 8 |
8 9 9 8 |
- Computar un análisis de varianza.
- Prueba de diferencias entre los cuatro niveles de\(B\) uso de la corrección de Bonferroni.
- Pruebe el componente lineal de tendencia para el efecto de\(B\).
- Trazar la interacción.
- Describir la interacción en palabras.
Q23
¿Por qué los diseños dentro de los sujetos suelen ser más potentes que el diseño entre sujetos?
Q24
Qué fuente de variación se encuentra en una tabla de resumen de ANOVA para un diseño dentro de sujetos que no está en una tabla de resumen de ANOVA para un diseño entre sujetos. ¿Qué sucede con esta fuente de variación en un diseño entre sujetos?
Q25
Los siguientes datos contienen tres puntuaciones de cada uno de los cinco sujetos. Los tres puntajes por materia son sus puntuaciones en tres ensayos de una tarea de memoria.
\[\begin{matrix} 4 & 6 & 7\\ 3 & 7 & 7\\ 2 & 8 & 5\\ 1 & 4 & 7\\ 4 & 6 & 9 \end{matrix}\]
- Computar un ANOVA
- Pruebe todas las diferencias por pares entre medias usando la prueba de Bonferroni al\(0.01\) nivel.
- Pruebe los componentes lineales y cuadráticos de tendencia para estos datos.
Q26
Indique las columnas fuente y df de la tabla de resumen de ANOVA para los siguientes experimentos:
- \(22\)cada uno de los sujetos se prueba en una tarea simple de tiempo de reacción y en una tarea de tiempo de reacción de elección.
- \(12\)los sujetos masculinos y\(12\) femeninos se prueban cada uno bajo tres niveles de dosificación del fármaco:\(0 mg, 10 mg, 20 mg\).
- \(20\)los sujetos se prueban en una tarea de aprendizaje motor para\(3\) ensayos diarios durante\(2\) días.
- Se realiza un experimento en el que las personas deprimidas son asignadas a un grupo de terapia farmacológica, a un grupo de terapia conductual o a un grupo de control. \(10\)asignaturas se asignan a cada grupo. El nivel de medido una vez al mes durante\(4\) meses.
Preguntas de casos prácticos
La siguiente pregunta es del estudio de caso Stroop Interference.
Q27
El conjunto de datos tiene las puntuaciones (veces) para hombres y mujeres en cada una de las tres tareas.
- Hacer un\(Gender (2) \times Task (3)\) análisis de varianza.
- Trazar la interacción.
La siguiente pregunta es del estudio de caso de Tratamiento del TDAH.
Q28
Los datos tienen cuatro puntajes por tema.
- ¿El diseño es entre sujetos o dentro de los sujetos?
- Crear una tabla de resumen de ANOVA.
La siguiente pregunta es del estudio de caso Angry Moods.
Q29
Utilizando el Índice de Expresión de Anger como variable dependiente, realizar un\(2 \times 2\) ANOVA con género y participación deportiva como los dos factores. ¿Los atletas y los no atletas difieren significativamente en la cantidad de ira que expresan? ¿Los géneros difieren significativamente en el Índice de Expresión de Ira? ¿El efecto de la participación deportiva es significativamente diferente para los dos géneros?
La siguiente pregunta es del estudio de caso Armas y Agresión.
Q30
Calcular un\(2 \times 2\) ANOVA sobre estos datos con los siguientes dos factores: tipo primo (¿la primera palabra era un arma o no?) y tipo de palabra (¿la segunda palabra era agresiva o no agresiva?). Considere cuidadosamente si las variables son variables entre sujetos o dentro de los subectos.
La siguiente pregunta es del estudio de caso Sonrisas y clemencia.
Q31
Compute la tabla de resumen de ANOVA.


