17.1: Distribución Chi Square
- Page ID
- 152373
Objetivos de aprendizaje
- Definir la distribución de Chi Cuadrado en términos de desviaciones normales cuadradas
- Describir cómo cambia la forma de la distribución del Chi Square a medida que aumentan sus grados de libertad
Una desviación normal estándar es una muestra aleatoria de la distribución normal estándar. La distribución de Chi Cuadrado es la distribución de la suma de desviaciones normales estándar cuadradas. Los grados de libertad de la distribución es igual al número de desviaciones normales estándar que se están sumando. Por lo tanto, el Cuadrado Chi con un grado de libertad\(\chi ^2(1)\), escrito como, es simplemente la distribución de un solo cuadrado desviado normal. El área de una distribución de Chi Square a continuación\(4\) es la misma que el área de una distribución normal estándar a continuación\(2\), ya que\(4\) es\(2^2\).
Considera el siguiente ejemplo.
Ejemplo\(\PageIndex{1}\)
Muestra dos puntuaciones de una distribución normal estándar, cuadrar cada puntaje y sumar los cuadrados. ¿Cuál es la probabilidad de que la suma de estos dos cuadrados sea de seis o más?
Solución
Dado que se muestrean dos puntajes, la respuesta se puede encontrar usando la distribución Chi Square con dos grados de libertad. Se puede usar una calculadora de Chi Square para encontrar que la probabilidad de un Chi Square (con\(2 df\)) being six or higher is \(0.050\).
La media de una distribución de Chi Square son sus grados de libertad. Las distribuciones de Chi Square están sesgadas positivamente, con el grado de sesgo decreciente al aumentar los grados de libertad. A medida que aumentan los grados de libertad, la distribución de Chi Square se acerca a una distribución normal. La figura\(\PageIndex{1}\) muestra funciones de densidad para tres distribuciones de Chi Cuadrado. Observe cómo disminuye el sesgo a medida que aumentan los grados de libertad.
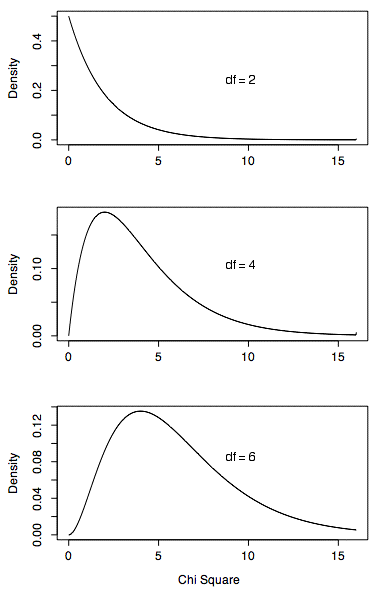
La distribución de Chi Square es muy importante porque muchas estadísticas de prueba se distribuyen aproximadamente como Chi Square. Dos de las pruebas más comunes que utilizan la distribución de Chi Cuadrado son pruebas de desviaciones de diferencias entre frecuencias teóricamente esperadas y observadas (tablas unidireccionales) y la relación entre variables categóricas (tablas de contingencia). Numerosas otras pruebas más allá del alcance de este trabajo se basan en la distribución de Chi Square.


