2.5: Parcelas de Caja
- Page ID
- 153238
Las gráficas de caja (también llamadas gráficas de caja y bigotes o gráficas de caja y bigotes) dan una buena imagen gráfica de la concentración de los datos. También muestran qué tan lejos están los valores extremos de la mayoría de los datos. Se construye una gráfica de caja a partir de cinco valores: el valor mínimo, el primer cuartil, la mediana, el tercer cuartil y el valor máximo. Utilizamos estos valores para comparar qué tan cerca están otros valores de datos de ellos.
Para construir una gráfica de caja, utilice una recta numérica horizontal o vertical y una caja rectangular. Los valores de datos más pequeños y mayores etiquetan los puntos finales del eje. El primer cuartil marca un extremo de la caja y el tercer cuartil marca el otro extremo de la caja. Aproximadamente el 50 por ciento medio de los datos caen dentro de la caja. Los “bigotes” se extienden desde los extremos de la caja hasta los valores de datos más pequeños y mayores. La mediana o segundo cuartil puede estar entre el primer y tercer cuartil, o puede ser uno, o el otro, o ambos. El diagrama de caja da una buena y rápida imagen de los datos.
Puede encontrar parcelas de caja y bigotes que tienen puntos que marcan valores atípicos. En esos casos, los bigotes no se extienden a los valores mínimo y máximo.
Consideremos, nuevamente, este conjunto de datos.
1; 1; 2; 2; 4; 6; .8; 7.2; 8; 8.3; 9; 10; 10; 11.5
El primer cuartil es dos, la mediana es siete y el tercer cuartil es nueve. El valor más pequeño es uno, y el valor más grande es 11.5. La siguiente imagen muestra la gráfica de caja construida.
Consulte las instrucciones de la calculadora en el sitio web de TI o en el apéndice.

Los dos bigotes se extienden desde el primer cuartil hasta el valor más pequeño y desde el tercer cuartil hasta el mayor valor. La mediana se muestra con una línea discontinua.
Es importante iniciar una gráfica de caja con una recta numérica escalada. De lo contrario, la gráfica de caja puede no ser útil.
Ejemplo\(\PageIndex{1}\)
Los siguientes datos son las alturas de 40 alumnos en una clase de estadística.
59; 60; 61; 62; 62; 63; 63; 64; 64; 64; 65; 65; 65; 65; 65; 65; 65; 65; 65; 65; 65; 65; 66; 66; 67; 67; 68; 68; 69; 70; 70; 70; 70; 70; 70; 71; 71; 72; 72; 73; 74; 74; 75; 77
Construir un diagrama de caja con las siguientes propiedades; las instrucciones de la calculadora para los valores mínimo y máximo así como los cuartiles siguen el ejemplo.
- Valor mínimo = 59
- Valor máximo = 77
- Q 1: Primer cuartil = 64.5
- Q 2: Segundo cuartil o mediana= 66
- Q 3: Tercer cuartil = 70

- Cada trimestre tiene aproximadamente el 25% de los datos.
- Los diferenciales de los cuatro trimestres son 64.5 — 59 = 5.5 (primer trimestre), 66 — 64.5 = 1.5 (segundo trimestre), 70 — 66 = 4 (tercer trimestre) y 77 — 70 = 7 (cuarto trimestre). Entonces, el segundo trimestre tiene el spread más pequeño y el cuarto trimestre tiene el spread más grande.
- \(\text{Range} = \text{maximum value} - \text{the minimum value} = 77 - 59 = 18\)
- Rango intercuartílico:\(IQR = Q_{3} – Q_{1} = 70 - 64.5 = 5.5\).
- El intervalo 59—65 tiene más del 25% de los datos por lo que tiene más datos en él que el intervalo 66 al 70 que tiene 25% de los datos.
- El 50% medio (mitad media) de los datos tiene un rango de 5.5 pulgadas.
Calculadora
Para encontrar el mínimo, el máximo y los cuartiles:
Ingresa datos en el editor de listas (Pres STAT 1:EDIT). Si necesita borrar la lista, flecha hacia arriba hasta el nombre L1, presione CLEAR y luego flecha hacia abajo.
Poner los valores de datos en la lista L1.
Presione STAT y flecha hacia CALC. Prensa 1:1 -VarStats. Ingresa L1.
Presione ENTER.
Utilice las teclas de flecha hacia abajo y hacia arriba para desplazarse.
Valor más pequeño = 59.
Valor mayor = 77.
Q 1: Primer cuartil = 64.5.
Q 2: Segundo cuartil o mediana = 66.
Q 3: Tercer cuartil = 70.
Para construir la gráfica de caja:
Prensa 4: Plotsoff. Presione ENTER.
Flecha hacia abajo y luego usa la tecla de flecha derecha para ir a la quinta imagen, que es la trama de caja. Presione ENTER.
Flecha hacia abajo a Xlist: Presiona 2nd 1 para L1
Flecha abajo a Freq: Presiona ALPHA. Presione 1.
Presiona Zoom. Presione 9: ZoomStat.
Presione TRACE y use las teclas de flecha para examinar la gráfica de caja.
Ejercicio\(\PageIndex{1}\)
Los siguientes datos son el número de páginas en 40 libros en una estantería. Construya una gráfica de caja usando una calculadora gráfica y establezca el rango intercuartílico.
136; 140; 178; 190; 205; 215; 217; 218; 232; 234; 240; 255; 270; 275; 290; 301; 303; 315; 317; 318; 326; 333; 343; 349; 360; 369; 377; 388; 391; 392; 398; 400; 402; 405; 408; 422; 429; 450; 475; 512
Contestar

\(IQR = 158\)
Para algunos conjuntos de datos, algunos del valor más grande, el valor más pequeño, el primer cuartil, la mediana y el tercer cuartil pueden ser los mismos. Por ejemplo, podrías tener un conjunto de datos en el que la mediana y el tercer cuartil sean iguales. En este caso, el diagrama no tendría una línea punteada dentro del cuadro mostrando la mediana. El lado derecho de la caja mostraría tanto el tercer cuartil como la mediana. Por ejemplo, si el valor más pequeño y el primer cuartil fueran ambos uno, la mediana y el tercer cuartil eran ambos cinco, y el valor más grande era siete, la gráfica de caja se vería así:
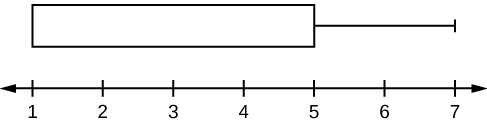
En este caso, al menos 25% de los valores son iguales a uno. El veinticinco por ciento de los valores se encuentran entre uno y cinco, inclusive. Al menos 25% de los valores son iguales a cinco. El 25% superior de los valores caen entre cinco y siete, inclusive.
Ejemplo\(\PageIndex{2}\)
Los puntajes de las pruebas para una clase universitaria de estadística realizada durante el día son:
99; 56; 78; 55.5; 32; 90; 80; 81; 56; 59; 45; 77; 84.5; 84; 70; 72; 68; 32; 79; 90
Los puntajes de las pruebas para una clase de estadística universitaria realizada durante la noche son:
98; 78; 68; 83; 81; 89; 88; 76; 65; 45; 98; 90; 80; 84.5; 85; 79; 78; 98; 90; 79; 81; 25.5
- Encuentra los valores más pequeños y mayores, la mediana y el primer y tercer cuartil para la clase de día.
- Encuentra los valores más pequeños y mayores, la mediana y el primer y tercer cuartil para la clase nocturna.
- Para cada conjunto de datos, ¿qué porcentaje de los datos se encuentra entre el valor más pequeño y el primer cuartil? el primer cuartil y la mediana? la mediana y el tercer cuartil? el tercer cuartil y el mayor valor? ¿Qué porcentaje de los datos se encuentra entre el primer cuartil y el mayor valor?
- Cree una gráfica de caja para cada conjunto de datos. Utilice una línea numérica para ambas parcelas de caja.
- ¿Qué gráfica de caja tiene la dispersión más amplia para el 50% medio de los datos (los datos entre el primer y tercer cuartiles)? ¿Qué significa esto para ese conjunto de datos en comparación con el otro conjunto de datos?
Contestar
-
- Mín = 32
- Q 1 = 56
- M = 74.5
- Q 3 = 82.5
- Máx = 99
-
- Mín = 25.5
- Q 1 = 78
- M = 81
- Q 3 = 89
- Máx = 98
- Clase diurna: Hay seis valores de datos que van de 32 a 56:30%. Hay seis valores de datos que van de 56 a 74.5:30%. Hay cinco valores de datos que van de 74.5 a 82.5:25%. Hay cinco valores de datos que van de 82.5 a 99:25%. Hay 16 valores de datos entre el primer cuartil, 56, y el valor más grande, 99:75%. Clase Nocturna:
-
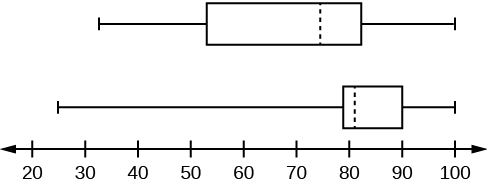
Figura\(\PageIndex{5}\)
- El primer conjunto de datos tiene la dispersión más amplia para el 50% medio de los datos. El IQR para el primer conjunto de datos es mayor que el IQR para el segundo conjunto. Esto significa que hay más variabilidad en el medio 50% del primer conjunto de datos.
Ejercicio\(\PageIndex{2}\)
El siguiente conjunto de datos muestra las alturas en pulgadas para los chicos en una clase de 40 alumnos.
66; 66; 67; 67; 68; 68; 68; 68; 68; 69; 69; 69; 70; 71; 72; 72; 72; 73; 73; 74
El siguiente conjunto de datos muestra las alturas en pulgadas para las niñas en una clase de 40 alumnos.
61; 61; 62; 62; 63; 63; 63; 65; 65; 65; 66; 66; 66; 67; 68; 68; 68; 69; 69; 69; 69
Construya una gráfica de caja usando una calculadora gráfica para cada conjunto de datos, y establezca qué gráfica de caja tiene la dispersión más amplia para el 50% medio de los datos.
Contestar

IQR para los chicos = 4
IQR para las chicas = 5
La gráfica de caja para las alturas de las niñas tiene la extensión más amplia para el 50% medio de los datos.
Ejemplo\(\PageIndex{3}\)
Grafique una gráfica de caja y bigotes para los valores de datos mostrados.
10; 10; 10; 15; 35; 75; 90; 95; 100; 175; 420; 490; 515; 515; 790
Los cinco números utilizados para crear una gráfica de caja y bigotes son:
- Mín: 10
- Q 1:15
- Med: 95
- Q 3: 490
- Máx.: 790
La siguiente gráfica muestra la gráfica de caja y bigotes.

Ejercicio\(\PageIndex{3}\)
Siga los pasos que utilizó para graficar una gráfica de caja y bigotes para los valores de datos mostrados.
0; 5; 5; 15; 30; 30; 45; 50; 50; 60; 75; 110; 140; 240; 330
Contestar
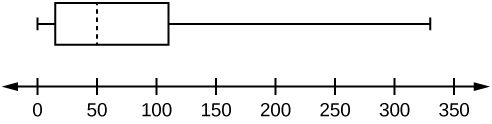
Los datos están en orden de menor a mayor. Hay 15 valores, por lo que el octavo número en orden es la mediana: 50. Hay siete valores de datos escritos a la izquierda de la mediana y 7 valores a la derecha. Los cinco valores que se utilizan para crear la gráfica de caja son:
- Mín: 0
- Q 1:15
- Med: 50
- Q 3: 110
- Máx.: 330
Referencias
- Datos de la revista West.
Revisar
Las gráficas de caja son un tipo de gráfico que puede ayudar a organizar visualmente los datos. Para graficar una gráfica de caja se deben calcular los siguientes puntos de datos: el valor mínimo, el primer cuartil, la mediana, el tercer cuartil y el valor máximo. Una vez que se grafica la gráfica de caja, puede mostrar y comparar distribuciones de datos.
A sesenta y cinco vendedores de autos seleccionados al azar se les preguntó el número de autos que generalmente venden en una semana. Catorce personas respondieron que generalmente venden tres autos; diecinueve generalmente venden cuatro autos; doce generalmente venden cinco autos; nueve generalmente venden seis autos; once generalmente venden siete autos.
Ejercicio 2.5.4
Construye un diagrama de caja debajo. Usa una regla para medir y escalar con precisión.
Ejercicio 2.5.5
Al mirar tu parcela de caja, ¿parece que los datos se concentran juntos, se distribuyen de manera uniforme o se concentran en algunas áreas, pero no en otras? ¿Cómo se puede decir?
Contestar
Más del 25% de los vendedores venden cuatro autos en una semana típica. Se puede ver esta concentración en la gráfica de caja porque el primer cuartil es igual a la mediana. El 25% superior y el 25% inferior se extienden uniformemente; los bigotes tienen la misma longitud.
Reuniéndolo
Ejercicio 2.5.6
El condado de Santa Clara, CA, tiene aproximadamente 27,873 japoneses-estadounidenses. Sus edades son las siguientes:
| Grupo de edad | Porcentaje de Comunidad |
|---|---|
| 0—17 | 18.9 |
| 18—24 | 8.0 |
| 25—34 | 22.8 |
| 35—44 | 15.0 |
| 45—54 | 13.1 |
| 55—64 | 11.9 |
| 65+ | 10.3 |
- Construir un histograma de la comunidad japonesa-estadounidense en el condado de Santa Clara, CA. Las barras no tendrán el mismo ancho para este ejemplo. ¿Por qué no? ¿Qué impacto tiene esto en la confiabilidad de la gráfica?
- ¿Qué porcentaje de la comunidad es menor de 35 años?
- ¿Qué trama de caja se parece más a la información anterior?
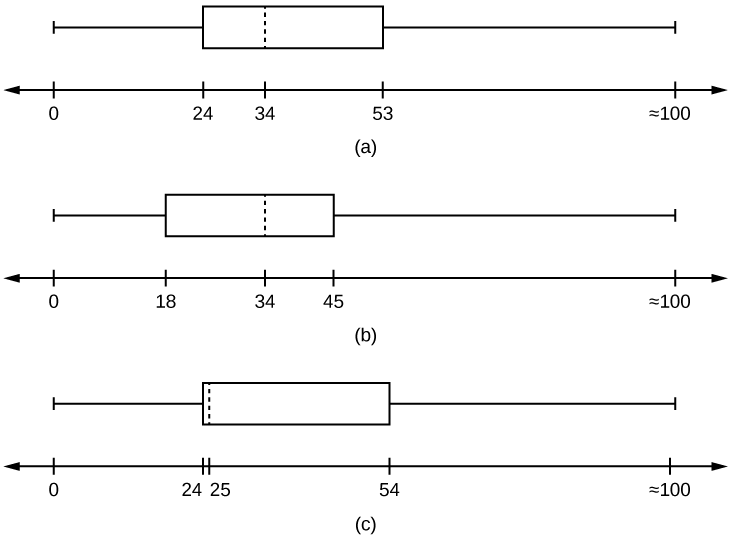
Contestar
- Para la gráfica, consulta la solución del estudiante.
- El 49.7% de la comunidad es menor de 35 años.
- Con base en la información de la tabla, la gráfica (a) representa más de cerca los datos.
Glosario
- Parcela de caja
- un gráfico que da una imagen rápida del 50% medio de los datos
- Primer cuartil
- el valor que es la mediana de la de la mitad inferior del conjunto de datos ordenado
- Polígono de frecuencia
- parece un gráfico de líneas pero usa intervalos para mostrar rangos de grandes cantidades de datos
- Intervalo
- también llamado intervalo de clase; un intervalo representa un rango de datos y se usa cuando se muestran conjuntos de datos grandes
- Conjunto de datos emparejados
- dos conjuntos de datos que tienen una relación uno a uno para que:
-
- ambos conjuntos de datos son del mismo tamaño, y
- cada punto de datos en un conjunto de datos coincide exactamente con un punto del otro conjunto.
- sesgado
- utilizado para describir datos que no son simétricos; cuando el lado derecho de una gráfica se ve “recortado” comparado con el lado izquierdo, decimos que está “sesgado a la izquierda”. Cuando el lado izquierdo de la gráfica se ve “picado” en comparación con el lado derecho, decimos que los datos están “sesgados hacia la derecha”. Alternativamente: cuando los valores más bajos de los datos están más dispersos, decimos que los datos están sesgados hacia la izquierda. Cuando los valores mayores están más dispersos, los datos están sesgados hacia la derecha.


