5.1: Introducción
- Page ID
- 153262
Objetivos del Capítulo
Al final de este capítulo, el alumno deberá ser capaz de:
- Reconocer y comprender las funciones continuas de densidad de probabilidad en general.
- Reconocer la distribución uniforme de probabilidad y aplicarla adecuadamente.
- Reconocer la distribución exponencial de probabilidad y aplicarla adecuadamente.
Las variables aleatorias continuas tienen muchas aplicaciones. Los promedios de bateo de béisbol, los puntajes de coeficiente intelectual, el tiempo que dura una llamada telefónica de larga distancia, la cantidad de dinero que lleva una persona, el tiempo que dura un chip de computadora y los puntajes del SAT son solo algunos. El campo de confiabilidad depende de una variedad de variables aleatorias continuas.
Los valores de las variables aleatorias discretas y continuas pueden ser ambiguos. Por ejemplo, si\(X\) es igual al número de millas (a la milla más cercana) que conduces para trabajar, entonces\(X\) es una variable aleatoria discreta. Usted cuenta las millas. Si\(X\) es la distancia que conduces para trabajar, entonces mides valores de\(X\) y\(X\) es una variable aleatoria continua. Para un segundo ejemplo, si\(X\) es igual al número de libros en una mochila, entonces\(X\) es una variable aleatoria discreta. Si\(X\) es el peso de un libro, entonces\(X\) es una variable aleatoria continua porque se miden los pesos. La forma en que se define la variable aleatoria es muy importante.

Propiedades de las Distribuciones de Probabilidad Continua
La gráfica de una distribución de probabilidad continua es una curva. La probabilidad se representa por el área bajo la curva. La curva se llama la función de densidad de probabilidad (abreviada como pdf). Usamos el símbolo\(f(x)\) para representar la curva. \(f(x)\)es la función que corresponde a la gráfica; utilizamos la función de densidad\(f(x)\) para dibujar la gráfica de la distribución de probabilidad. El área bajo la curva viene dada por una función diferente llamada función de distribución acumulativa (abreviada como cdf). La función de distribución acumulativa se utiliza para evaluar la probabilidad como área.
- Los resultados se miden, no se cuentan.
- Toda el área bajo la curva y por encima del eje x es igual a uno.
- La probabilidad se encuentra para intervalos de\(x\) valores en lugar de para\(x\) valores individuales.
- \(P(c < x < d)\)es la probabilidad de que la variable aleatoria\(X\) esté en el intervalo entre los valores\(c\) y\(d\). \(P(c < x < d)\)es el área bajo la curva, por encima del eje x, a la derecha\(c\) y a la izquierda de\(d\).
- \(P(x = c) = 0\)La probabilidad de que\(x\) tome cualquier valor individual individual es cero. El área por debajo de la curva, por encima del eje x, y entre\(x = c\) y no\(x = c\) tiene ancho, y por lo tanto no tiene área (área = 0). Dado que la probabilidad es igual al área, la probabilidad también es cero.
- \(P(c < x < d)\)es lo mismo que\(P(c \leq x \leq d)\) porque la probabilidad es igual al área.
Encontraremos el área que representa la probabilidad mediante el uso de geometría, fórmulas, tecnología o tablas de probabilidad. En general, se necesita cálculo para encontrar el área bajo la curva para muchas funciones de densidad de probabilidad. Cuando utilizamos fórmulas para encontrar el área en este libro de texto, las fórmulas se encontraron utilizando las técnicas de cálculo integral. Sin embargo, debido a que la mayoría de los estudiantes que toman este curso no han estudiado cálculo, no vamos a usar cálculo en este libro de texto. Hay muchas distribuciones continuas de probabilidad. Cuando se utiliza una distribución de probabilidad continua para modelar la probabilidad, la distribución utilizada se selecciona para modelar y ajustar la situación particular de la mejor manera.
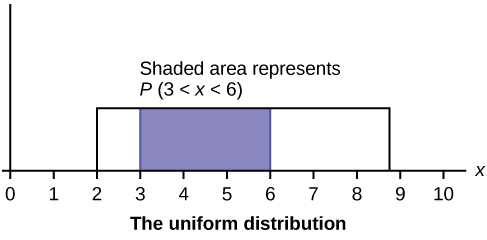
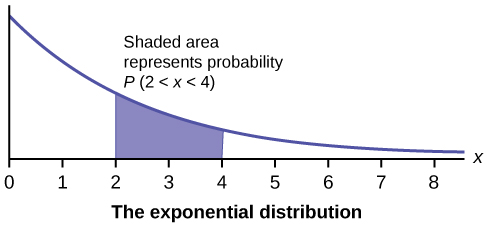
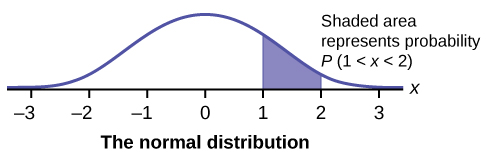
En este capítulo y en el siguiente, estudiaremos la distribución uniforme, la distribución exponencial y la distribución normal. Las siguientes gráficas ilustran estas distribuciones.
Glosario
- Distribución Uniforme
- una variable aleatoria continua (RV) que tiene resultados igualmente probables sobre el dominio,\(a < x < b\); a menudo se le conoce como la distribución rectangular porque la gráfica del pdf tiene la forma de un rectángulo. Notación:\(X \sim U(a,b)\). La media es\(\mu = \frac{a+b}{2}\) y la desviación estándar es\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\). La función de densidad de probabilidad es\(f(x) = \frac{1}{b-a}\) para\(a < x < b\) o\(a \leq x \leq b\). La distribución acumulativa es\(P(X \leq x) = \frac{x-a}{b-a}\).
- Distribución Exponencial
- una variable aleatoria continua (RV) que aparece cuando estamos interesados en los intervalos de tiempo entre algunos eventos aleatorios, por ejemplo, el tiempo entre llegadas de emergencia a un hospital; la notación es\(X \sim \text{Exp}(m)\). La media es\(\mu = \frac{1}{m}\) y la desviación estándar es\(\sigma = \frac{1}{m}\). La función de densidad de probabilidad es\(f(x) = me^{-mx}\),\(x \geq 0\) y la función de distribución acumulativa es\(P(X \leq x) = 1 − e^{mx}\).


