1.1: Definiciones y conceptos básicos
- Page ID
- 151087
Objetivos de aprendizaje
- Conocer las definiciones básicas utilizadas en la estadística y algunos de sus conceptos clave.
Comenzamos con un ejemplo sencillo. Hay millones de automóviles de pasajeros en Estados Unidos. ¿Cuál es su valor promedio? Obviamente, no es práctico intentar resolver este problema directamente evaluando el valor de cada automóvil en el país, sumar todos esos valores, luego dividir por el número de valores, uno por cada automóvil. En la práctica lo mejor que podemos hacer sería estimar el valor promedio. Una forma natural de hacerlo sería seleccionar aleatoriamente algunos de los autos, digamos\(200\) de ellos, determinar el valor de cada uno de esos autos y encontrar el promedio de esos\(200\) valores. Al conjunto de todos esos millones de vehículos se le llama la población de interés, y el número adjunto a cada uno, su valor, es una medida. El valor promedio es un parámetro: un número que describe una característica de la población, en este caso el valor monetario. El conjunto de\(200\) autos seleccionados de la población se llama muestra, y los\(200\) números, los valores monetarios de los autos que seleccionamos, son los datos de la muestra. El promedio de los datos se llama estadística: un número calculado a partir de los datos de la muestra. Este ejemplo ilustra el significado de las siguientes definiciones.
Definiciones: poblaciones y muestras
Una población es cualquier colección específica de objetos de interés. Una muestra es cualquier subconjunto o subcolección de la población, incluyendo el caso de que la muestra esté conformada por toda la población, en cuyo caso se denomina censo.
Definiciones: mediciones y datos de muestra
Una medición es un número o atributo calculado para cada miembro de una población o de una muestra. Las mediciones de los elementos de muestra se denominan colectivamente los datos de muestra.
Definición: parámetros
Un parámetro es un número que resume algún aspecto de la población en su conjunto. Una estadística es un número calculado a partir de los datos de la muestra.
Continuando con nuestro ejemplo, si el valor promedio de los autos en nuestra muestra fue\($8,357\), entonces parece razonable concluir que el valor promedio de todos los autos es de aproximadamente\($8,357\). Al razonar de esta manera hemos hecho una inferencia sobre la población a partir de la información obtenida de la muestra. En general, la estadística es un estudio de datos: describir las propiedades de los datos, lo que se denomina estadística descriptiva, y sacar conclusiones sobre una población de interés a partir de información extraída de una muestra, la cual se denomina inferencial estadísticas. El cálculo del número único\($8,357\) para resumir los datos fue una operación de estadística descriptiva; utilizarla para hacer una declaración sobre la población fue una operación de estadística inferencial.
Definición: Estadísticas
La estadística es una colección de métodos para recopilar, mostrar, analizar y sacar conclusiones a partir de datos.
Definición: Estadística descriptiva
La estadística descriptiva es la rama de la estadística que consiste en organizar, mostrar y describir datos.
Definición: Estadísticas inferenciales
La estadística inferencial es la rama de la estadística que implica sacar conclusiones sobre una población a partir de la información contenida en una muestra tomada de esa población.
Definición: Datos cualitativos
Los datos cualitativos son medidas para las que no existe una escala numérica natural, sino que consisten en atributos, etiquetas u otras características no numéricas.
Definición: Datos cuantitativos
Los datos cuantitativos son medidas numéricas que surgen de una escala numérica natural.
Los datos cualitativos pueden generar estadísticas numéricas de muestras. En el ejemplo del automóvil, por ejemplo, podríamos estar interesados en la proporción de todos los autos que tienen menos de seis años de antigüedad. En nuestra misma muestra de\(200\) autos podríamos anotar por cada auto si tiene menos de seis años o no, lo cual es una medida cualitativa. Si\(172\) los autos en la muestra tienen menos de seis años, que es\(0.86\) o\(86\% \), entonces estimaríamos que el parámetro de interés, la proporción poblacional, sea aproximadamente el mismo que el estadístico muestral, la proporción muestral, es decir, aproximadamente\(0.86\).
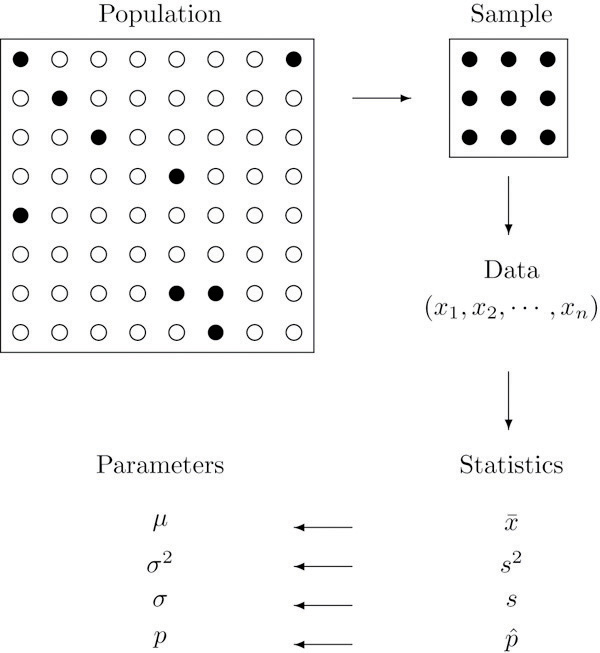
La relación entre una población de interés y una muestra extraída de esa población es quizás el concepto más importante en la estadística, ya que todo lo demás descansa en él. Esta relación se ilustra gráficamente en la Figura\(\PageIndex{1}\). Los círculos en la caja grande representan elementos de la población. En la figura solo había espacio para un pequeño número de ellos pero en situaciones reales, como nuestro ejemplo automovilístico, muy bien podrían contabilizar en millones. Los círculos negros sólidos representan los elementos de la población que se seleccionan al azar y que juntos forman la muestra. Para cada elemento de la muestra hay una medida de interés, denotada por una\(x\) minúscula (que hemos indexado\(x_1 , \ldots, x_n\) para distinguirlos); estas mediciones forman colectivamente el conjunto de datos de la muestra. A partir de los datos podemos calcular diversas estadísticas. Para anticipar la notación que se utilizará posteriormente, podríamos calcular la media muestral\(\bar{x}\) y la proporción muestral\(\hat{p}\), y tomarlas como aproximaciones a la media poblacional\(\mu\) (esta es la letra griega minúscula mu, el símbolo tradicional para este parámetro) y la población proporción\(p\), respectivamente. Los otros símbolos en la figura representan otros parámetros y estadísticas que encontraremos.
Llave para llevar
- La estadística es un estudio de datos: describiendo las propiedades de los datos (estadística descriptiva) y sacando conclusiones sobre una población a partir de la información de una muestra (estadística inferencial).
- La distinción entre una población junto con sus parámetros y una muestra junto con sus estadísticas es un concepto fundamental en la estadística inferencial.
- La información en una muestra se utiliza para hacer inferencias sobre la población de la que se extrajo la muestra.

