9.2: Comparación de dos medias poblacionales - Muestras pequeñas e independientes
- Page ID
- 151119
Objetivos de aprendizaje
- Aprender a construir un intervalo de confianza para la diferencia en las medias de dos poblaciones distintas utilizando muestras pequeñas e independientes.
- Aprender a realizar una prueba de hipótesis sobre la diferencia entre las medias de dos poblaciones distintas utilizando muestras pequeñas e independientes.
Cuando uno u otro de los tamaños de muestra es pequeño, como suele ser el caso en la práctica, el Teorema del Límite Central no aplica. Debemos entonces imponer condiciones a la población para darle validez estadística al procedimiento de prueba. Supondremos que ambas poblaciones de las que se toman las muestras tienen una distribución de probabilidad normal y que sus desviaciones estándar son iguales.
Intervalos de confianza
Cuando las dos poblaciones están normalmente distribuidas y tienen desviaciones estándar iguales,\(\mu _1-\mu _2\) es válida la siguiente fórmula para un intervalo de confianza para.
\(100(1-\alpha )\%\) Confidence Interval for the Difference Between Two Population Means: Small, Independent Samples
\[(\bar{x_1}-\bar{x_2})\pm t_{\alpha /2}\sqrt{s_{p}^{2}\left ( \dfrac{1}{n_1}+\dfrac{1}{n_2} \right )} \label{eq1}\]
donde
\[s_{p}^{2}=\dfrac{(n_1-1)s_{1}^{2}+(n_2-1)s_{2}^{2}}{n_1+n_2-2}\]
El número de grados de libertad es
\[df=n_1+n_2-2.\]
Las muestras deben ser independientes, las poblaciones deben ser normales y las desviaciones estándar de la población deben ser iguales. Muestras “pequeñas” significa que cualquiera\(n_1<30\) o\(n_2<30\).
La cantidad\(s_{p}^{2}\) se denomina varianza de muestra agrupada. Es un promedio ponderado de las dos estimaciones\(s_{1}^{2}\) y\(s_{2}^{2}\) de la varianza común\(\sigma _{1}^{2}=\sigma _{2}^{2}\) de las dos poblaciones.
Ejemplo\(\PageIndex{1}\)
Una compañía de software comercializa un nuevo juego de computadora con dos diseños experimentales de empaque. \(1\)El diseño se envía a\(11\) las tiendas; sus ventas promedio el primer mes son\(52\) unidades con unidades de desviación\(12\) estándar de muestra. \(2\)El diseño se envía a\(6\) las tiendas; sus ventas promedio el primer mes son\(46\) unidades con unidades de desviación\(10\) estándar de muestra. Construir una estimación de puntos y un intervalo de\(95\%\) confianza para la diferencia en las ventas mensuales promedio entre los dos diseños de paquetes.
Solución:
La estimación puntual de\(\mu _1-\mu _2\) es
\[\bar{x_1}-\bar{x_2}=52-46-6 \nonumber\]
En palabras, estimamos que las ventas mensuales promedio para Diseño\(1\) son\(6\) unidades más al mes que las ventas mensuales promedio para Diseño\(2\).
Para aplicar la fórmula para el intervalo de confianza (Ecuación\ ref {eq1}), debemos encontrar\(t_{\alpha /2}\). El nivel de\(95\%\) confianza significa\(\alpha =1-0.95=0.05\) eso para que\(t_{\alpha /2}=t_{0.025}\). De la Figura 7.1.6, en la fila con el encabezamiento\(df=11+6-2=15\) leemos eso\(t_{0.025}=2.131\). A partir de la fórmula para la varianza de muestra agrupada calculamos
\[s_{p}^{2}=\dfrac{(n_1-1)s_{1}^{2}+(n_2-1)s_{2}^{2}}{n_1+n_2-2}=\dfrac{(10)(12)^2+(5)(10)^2}{15}=129.\bar{3} \nonumber\]
Así
\[(\bar{x_1}-\bar{x_2})\pm t_\alpha /2\sqrt{s_{p}^{2}\left ( \dfrac{1}{n_1}+\dfrac{1}{n_2} \right )}=6\pm (2.131)\sqrt{129.\bar{3}\left ( \dfrac{1}{11}+\dfrac{1}{6} \right )}\approx 6\pm 12.3 \nonumber\]
Estamos\(95\%\) seguros de que la diferencia en las medias poblacionales radica en el intervalo\([-6.3,18.3]\), en el sentido de que en el muestreo repetido\(95\%\) de todos los intervalos construidos a partir de la muestra los datos de esta manera contendrán\(\mu _1-\mu _2\). Debido a que el intervalo contiene valores tanto positivos como negativos la afirmación en el contexto del problema es que estamos\(95\%\) seguros de que el promedio de ventas mensuales para Diseño\(1\) es entre\(18.3\) unidades superiores y\(6.3\) unidades inferiores a las ventas mensuales promedio para Diseño \(2\).
Prueba de Hipótesis
Las hipótesis de prueba sobre la diferencia de dos medias poblacionales usando muestras pequeñas se realizan precisamente como se hace para muestras grandes, utilizando el siguiente estadístico de prueba estandarizado. También se deben cumplir las mismas condiciones en las poblaciones que se requirieron para construir un intervalo de confianza para la diferencia de las medias cuando se prueben las hipótesis.
Estadístico de prueba estandarizado para pruebas de hipótesis sobre la diferencia entre dos medias poblacionales: muestras pequeñas e independientes
\[T=\dfrac{(\bar{x_1}-\bar{x_2})-D_0}{\sqrt{s_{p}^{2}\left ( \dfrac{1}{n_1}+\dfrac{1}{n_2}\right )}}\]
donde
\[ s_{p}^{2}=\dfrac{(n_1-1)s_{1}^{2}+(n_2-1)s_{2}^{2}}{n_1+n_2-2}\]
El estadístico de prueba tiene la distribución t de Student con\(df=n_1+n_2-2\) grados de libertad.
Las muestras deben ser independientes, las poblaciones deben ser normales y las desviaciones estándar de la población deben ser iguales. Muestras “pequeñas” significa que cualquiera\(n_1<30\) o\(n_2<30\).
Ejemplo\(\PageIndex{2}\)
Consulte Ejemplo\(\PageIndex{1}\) relativo a la media de ventas mensuales para el mismo juego de computadora pero vendido con dos diseños de paquetes. Pruebe a\(1\%\) nivel de significancia si los datos proporcionan evidencia suficiente para concluir que las ventas medias mensuales de los dos diseños son diferentes. Utilizar el enfoque de valor crítico.
Solución:
- Paso 1. La prueba relevante es
\[H_0: \mu _1-\mu _2=0 \nonumber\]
vs.
\[H_a: \mu _1-\mu _2\neq 0\; \; @\; \; \alpha =0.01 \nonumber\]
- Paso 2. Dado que las muestras son independientes y al menos una es menor que\(30\) la estadística de prueba es
\[T=\dfrac{(\bar{x_1}-\bar{x_2})-D_0}{\sqrt{s_{p}^{2}\left ( \dfrac{1}{n_1}+\dfrac{1}{n_2}\right )}} \nonumber\]
que tiene la\(t\) distribución de Student con\(df=11+6-2=15\) grados de libertad.
- Paso 3. Insertar los datos y el valor\(D_0=0\) en la fórmula para el estadístico de prueba da
\[\begin{align*} T&=\dfrac{(\bar{x_1}-\bar{x_2})-D_0}{\sqrt{s_{p}^{2}\left ( \dfrac{1}{n_1}+\dfrac{1}{n_2}\right )}} \\[4pt] &=\dfrac{(52-46)-0}{\sqrt{129.\bar{3}\left ( \dfrac{1}{11}+\dfrac{1}{6} \right )}} \\[4pt] &=1.040 \end{align*}\]
- Paso 4. Dado que el símbolo en\(H_a\) es “\(\neq\)” esta es una prueba de dos colas, por lo que hay dos valores críticos,\(\pm t_{\alpha /2}=\pm t_{0.005}\). De la fila en la Figura 7.1.6 con el encabezado\(df=15\) leemos\(t_{0.005}=2.947\). La región de rechazo es\((-\infty ,-2.947]\cup [2.947,\infty )\).
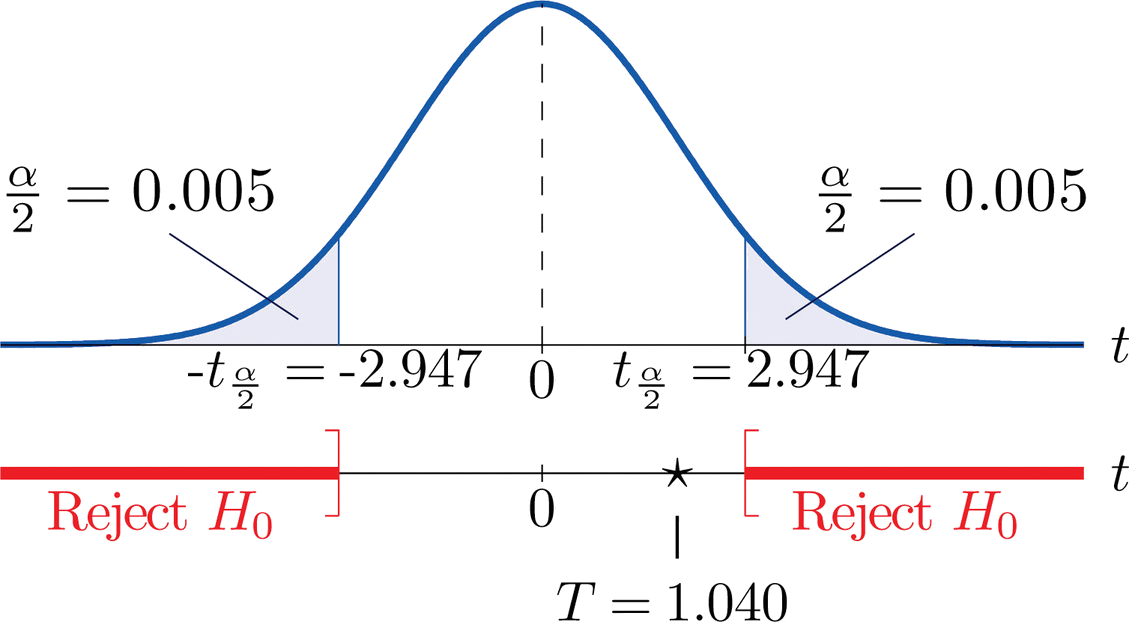
- Paso 5. Como se muestra en\(\PageIndex{1}\) la Figura el estadístico de prueba no cae en la región de rechazo. La decisión es no rechazar\(H_0\). En el contexto del problema nuestra conclusión es:
Los datos no aportan evidencia suficiente, a\(1\%\) nivel de significancia, para concluir que las ventas medias mensuales de los dos diseños son diferentes.
Ejemplo\(\PageIndex{3}\)
Realizar la prueba de Ejemplo\(\PageIndex{2}\) usando el enfoque\(p\) -value.
Solución:
Los tres primeros pasos son idénticos a los del Ejemplo\(\PageIndex{2}\).
- Paso 4. Debido a que la prueba es de dos colas la significancia observada o\(p\) -valor de la prueba es el doble del área de la cola derecha de la distribución del estudiante, con\(15\) grados de libertad, que es cortada por el estadístico de prueba\(T=1.040\). Sólo podemos aproximar este número. Mirando en la fila de la Figura 7.1.6 encabezada\(df=15\), el número\(1.040\) se encuentra entre los números\(0.866\) y\(1.341\), correspondiente a\(t_{0.200}\) y\(t_{0.100}\). El área cortada por\(t=0.866\) es\(0.200\) y el área cortada por\(t=1.341\) es\(0.100\). Ya que\(1.040\) está entre\(0.866\) y\(1.341\) el área que corta está entre\(0.200\) y\(0.100\). Por lo tanto, el\(p\) -valor (ya que el área debe duplicarse) está entre\(0.400\) y\(0.200\).
- Paso 5. Ya que\(p>0.200>0.01,\; \; p>\alpha\), así la decisión no es rechazar la hipótesis nula:
Los datos no aportan evidencia suficiente, a\(1\%\) nivel de significancia, para concluir que las ventas medias mensuales de los dos diseños son diferentes.
Llave para llevar
- En el contexto de estimar o probar hipótesis relativas a dos medias poblacionales, las muestras “pequeñas” significan que al menos una muestra es pequeña. En particular, aunque una muestra sea de tamaño\(30\) o más, si la otra es de tamaño menor que\(30\) las fórmulas de esta sección deben ser utilizadas.
- Se calcula un intervalo de confianza para la diferencia en dos medias poblacionales utilizando una fórmula de la misma manera que se hizo para una sola media poblacional.

