9.3: Comparación de dos medias poblacionales - muestras pareadas
- Page ID
- 151109
Objetivos de aprendizaje
- Conocer la distinción entre muestras independientes y muestras pareadas.
- Aprender a construir un intervalo de confianza para la diferencia en las medias de dos poblaciones distintas usando muestras pareadas.
- Aprender a realizar una prueba de hipótesis sobre la diferencia en las medias de dos poblaciones distintas usando muestras pareadas
Supongamos que los ingenieros químicos desean comparar el ahorro de combustible obtenido por dos formulaciones diferentes de gasolina. Dado que el ahorro de combustible varía ampliamente de un automóvil a otro, si se comparara la economía media de combustible de dos muestras independientes de vehículos que funcionan con los dos tipos de combustible, incluso si una formulación fuera mejor que la otra, la gran variabilidad de vehículo a vehículo podría hacer alguna diferencia derivada de la diferencia en el combustible difícil de detectar. Imagínese que una muestra aleatoria tiene muchos más vehículos grandes que la otra. En lugar de muestras aleatorias independientes, tendría más sentido seleccionar pares de autos de la misma marca y modelo y conducidos en circunstancias similares, y comparar el ahorro de combustible de los dos autos de cada par. Así los datos se verían algo así como Tabla\(\PageIndex{1}\), donde el primer automóvil de cada par es operado con una formulación del combustible (llámalo Tipo\(1\) gasolina) y el segundo carro es operado en el segundo (llámalo Tipo\(2\) gasolina).
| Marca y Modelo | Coche 1 | Coche 2 |
|---|---|---|
| Buick LaCrosse | 17.0 | 17.0 |
| Dodge Viper | 13.2 | 12.9 |
| Honda | 35.3 | 35.4 |
| Hummer H 3 | 13.6 | 13.2 |
| Lexus | 32.7 | 32.5 |
| Mazda CX-9 | 18.4 | 18.1 |
| Saab 9-3 | 22.5 | 22.5 |
| Toyota Corolla | 26.8 | 26.7 |
| Volvo XC 90 | 15.1 | 15.0 |
La primera columna de números forma una muestra de Población\(1\), la población de todos los autos operados con\(1\) gasolina Tipo; la segunda columna de números forma una muestra de Población\(2\), la población de todos los autos operados con\(2\) gasolina Tipo. Sería incorrecto analizar los datos utilizando las fórmulas de la sección anterior, sin embargo, ya que las muestras no se extrajeron de manera independiente. Lo correcto es calcular la diferencia en los números en cada par (restando en el mismo orden cada vez) para obtener la tercera columna de números como se muestra en Tabla\(\PageIndex{2}\) y tratar las diferencias como los datos. En este punto, la nueva muestra de diferencias\(d_1=0.0,\cdots ,d_9=0.1\) en la tercera columna de la Tabla\(\PageIndex{2}\) puede considerarse como una muestra aleatoria de tamaño\(n=9\) seleccionada de una población con media\(\mu _d=\mu _1-\mu _2\). Este enfoque esencialmente transforma el problema emparejado de dos muestras en un problema de una muestra como se discutió en los dos capítulos anteriores.
| Marca y Modelo | Coche 1 | Coche 2 | Diferencia |
|---|---|---|---|
| Buick LaCrosse | 17.0 | 17.0 | 0.0 |
| Dodge Viper | 13.2 | 12.9 | 0.3 |
| Honda | 35.3 | 35.4 | −0.1 |
| Hummer H 3 | 13.6 | 13.2 | 0.4 |
| Lexus | 32.7 | 32.5 | 0.2 |
| Mazda CX-9 | 18.4 | 18.1 | 0.3 |
| Saab 9-3 | 22.5 | 22.5 | 0.0 |
| Toyota Corolla | 26.8 | 26.7 | 0.1 |
| Volvo XC 90 | 15.1 | 15.0 | 0.1 |
Observe cuidadosamente que aunque no importa en qué orden se haga la resta, debe hacerse en el mismo orden para todos los pares. Es por ello que hay cantidades tanto positivas como negativas en la tercera columna de números en la Tabla\(\PageIndex{2}\).
Intervalos de confianza
Cuando la población de diferencias se distribuye normalmente es válida la siguiente fórmula para un intervalo de confianza para\(\mu _d=\mu _1-\mu _2\).
\(100(1−\alpha)\%\) Confidence Interval for the Difference Between Two Population Means: Paired Difference Samples
\[\bar{d}\pm t_{\alpha /2}\frac{s_d}{\sqrt{n}}\]
donde hay\(n\) pares,\(\bar{d}\) es la media y\(s_d\) es la desviación estándar de sus diferencias.
El número de grados de libertad es
\[df=n-1.\]
La población de diferencias debe estar normalmente distribuida.
Ejemplo\(\PageIndex{1}\)
Usando los datos de la Tabla\(\PageIndex{1}\) construir una estimación puntual y un intervalo de\(95\%\) confianza para la diferencia en el ahorro promedio de combustible entre los autos operados con\(1\) gasolina Tipo y los autos operados con\(2\) gasolina Tipo.
Solución:
Nos hemos referido a los datos en Table\(\PageIndex{1}\) porque esa es la forma en que los datos se presentan típicamente, pero enfatizamos que con el muestreo pareado uno calcula inmediatamente las diferencias, como se da en la Tabla\(\PageIndex{2}\), y usa las diferencias como los datos.
La media y desviación estándar de las diferencias son
\[\bar{d}=\frac{\sum d}{n}=\frac{1.3}{9}=0.1\bar{4}\]
\[s_d=\sqrt{\frac{\sum d^2-\frac{1}{n}(\sum d)^2}{n-1}}=\sqrt{\frac{0.41-\frac{1}{9}(1.3)^2}{8}}=0.1\bar{6}\]
La estimación puntual de\(\mu _1-\mu _2=\mu _d\) es
\[\bar{d}=0.14\]
En palabras, estimamos que la economía promedio de combustible de los autos que usan\(1\) gasolina Type es\(0.14\) mpg mayor que la economía promedio de combustible de los autos que usan\(2\) gasolina Type.
Para aplicar la fórmula para el intervalo de confianza, debemos encontrar\(t_{\alpha /2}\). El nivel de\(95\%\) confianza significa\(\alpha =1-0.95=0.05\) eso para que\(t_{\alpha /2}=t_{0.025}\). De la Figura 7.1.6, en la fila con el encabezamiento\(df=9-1=8\) leemos eso\(t_{0.025}=2.306\). Por lo tanto
\[\bar{d}\pm t_{\alpha /2}\frac{s_d}{\sqrt{n}}=0.14\pm 2.306\left ( \frac{0.1\bar{6}}{\sqrt{9}} \right )\approx 0.14\pm 0.13\]
Estamos\(95\%\) seguros de que la diferencia en las medias poblacionales radica en el intervalo\([0.01,0.27]\), en el sentido de que en el muestreo repetido\(95\%\) de todos los intervalos construidos a partir de la muestra los datos de esta manera contendrán\(\mu _d=\mu _1-\mu _2\). Dicho de otra manera, estamos\(95\%\) seguros de que la economía media de combustible es entre\(0.01\) y\(0.27\) mpg mayor con la\(1\) gasolina Tipo que con\(2\) la gasolina Tipo.
Prueba de Hipótesis
Las hipótesis de prueba sobre la diferencia de dos medias poblacionales usando muestras de diferencia pareadas se realizan precisamente como se hace para muestras independientes, aunque ahora las hipótesis nula y alternativa se expresan en términos de\(\mu _d\) lugar de\(\mu _1-\mu _2\). Así siempre se escribirá la hipótesis nula
\[H_0:\mu _d=D_0\]
Las tres formas de la hipótesis alternativa, con la terminología para cada caso, son:
| Forma de\(H_a\) | Terminología |
|---|---|
| \ (H_a\) "> \(H_a:\mu_d<D_0\) | Cola izquierda |
| \ (H_a\) ">\(H_a:\mu_d>D_0\) | Cola derecha |
| \ (H_a\) ">\(H_a:\mu_d\neq D_0\) | Dos colas |
También se deben cumplir las mismas condiciones en la población de diferencias que se requirieron para construir un intervalo de confianza para la diferencia de las medias cuando se prueben las hipótesis. Aquí está el estadístico de prueba estandarizado que se utiliza en la prueba.
Estadístico de prueba estandarizado para pruebas de hipótesis sobre la diferencia entre dos medias poblacionales: muestras de diferencia pareada
\[T=\frac{\bar{d}-D_0}{s_d/\sqrt{n}}\]
donde hay\(n\) pares,\(\bar{d}\) es la media y\(s_d\) es la desviación estándar de sus diferencias.
El estadístico de prueba tiene la\(t\) distribución de Student con\(df=n-1\) grados de libertad.
La población de diferencias debe estar normalmente distribuida.
Ejemplo\(\PageIndex{2}\): using the critical value approach
Usando los datos de la\(\PageIndex{2}\) prueba de Tabla la hipótesis de que la economía de combustible media para la\(1\) gasolina Tipo es mayor que la de la\(2\) gasolina Tipo contra la hipótesis nula de que las dos formulaciones de gasolina producen la misma economía media de combustible. Prueba a\(5\%\) nivel de significancia utilizando el enfoque de valor crítico.
Solución:
La única parte de la tabla que utilizamos es la tercera columna, las diferencias.
- Paso 1. Dado que las diferencias se calcularon en el orden\(\text{Type}\; \; 1 \; \; \text{mpg}-\text{Type}\; \; 2 \; \; \text{mpg}\), corresponde mejor economía de\(1\) combustible con combustible Type\(\mu _d=\mu _1-\mu _2>0\). Así la prueba es
\[H_0:\mu _d=0\\ \text{vs.}\\ H_a:\mu _d>0\; \; @\; \; \alpha =0.05\]
(Si las diferencias se hubieran calculado en el orden opuesto entonces las hipótesis alternativas habrían sido\(H_a:\mu _d<0\).)
- Paso 2. Dado que el muestreo es por pares, el estadístico de prueba es
\[T=\frac{\bar{d}-D_0}{s_d/\sqrt{n}}\]
- Paso 3. Ya hemos calculado\(\bar{d}\) y\(s_d\) en el ejemplo anterior. Insertar sus valores y\(D_0=0\) en la fórmula para el estadístico de prueba da
\[T=\frac{\bar{d}-D_0}{s_d/\sqrt{n}}=\frac{0.1\bar{4}}{0.1\bar{6}/\sqrt{3}}=2.600\]
- Paso 4. Dado que el símbolo en\(H_a\) es “\(>\)” esta es una prueba de cola derecha, por lo que hay un solo valor crítico,\(t_\alpha =t_{0.05}\) con\(8\) grados de libertad, que a partir de la fila etiquetada\(df=8\) en la Figura 7.1.6 leemos como\(1.860\). La región de rechazo es\([1.860,\infty )\).
- Paso 5. Como se muestra en\(\PageIndex{1}\) la Figura el estadístico de prueba cae en la región de rechazo. La decisión es rechazar\(H_0\). En el contexto del problema nuestra conclusión es:
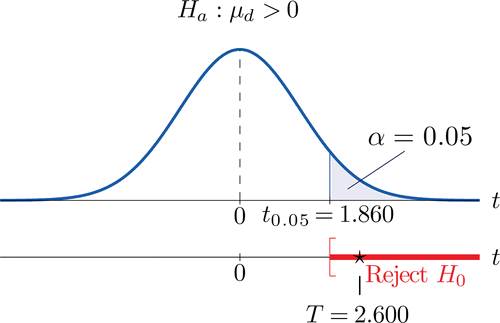
Los datos proporcionan evidencia suficiente, a\(5\%\) nivel de significancia, para concluir que la economía media de combustible proporcionada por la\(1\) gasolina Tipo es mayor que la de la\(2\) gasolina Tipo.
Ejemplo\(\PageIndex{3}\): using the p-value approach
Realizar la prueba en Ejemplo\(\PageIndex{2}\) usando el enfoque del valor p.
Solución:
Los tres primeros pasos son idénticos a esos\(\PageIndex{2}\).
- Paso 4. Debido a que la prueba es de una cola, la significancia observada o\(p\) -valor de la prueba es solo el área de la cola derecha de la\(t\) distribución de Student, con\(8\) grados de libertad, que es cortada por el estadístico de prueba\(T=2.600\). Sólo podemos aproximar este número. Mirando en la fila de la Figura 7.1.6 encabezada\(df=8\), el número\(2.600\) se encuentra entre los números\(2.306\) y\(2.896\), correspondiente a\(t_{0.025}\) y\(t_{0.010}\). El área cortada por\(t=2.306\) es\(0.025\) y el área cortada por\(t=2.896\) es\(0.010\). Ya que\(2.600\) está entre\(2.306\) y\(2.896\) el área que corta está entre\(0.025\) y\(0.010\). Así el\(p\) -valor está entre\(0.025\) y\(0.010\). En particular es menor que\(0.025\). Ver Figura\(\PageIndex{2}\).
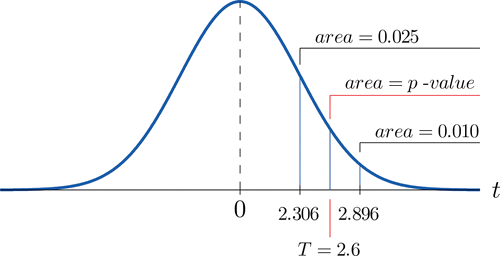
- Paso 5. Ya\(p<\alpha\) que\(0.025<0.05\), así la decisión es rechazar la hipótesis nula:
Los datos proporcionan evidencia suficiente, a\(5\%\) nivel de significancia, para concluir que la economía media de combustible proporcionada por la\(1\) gasolina Tipo es mayor que la de la\(2\) gasolina Tipo.
El experimento emparejado de dos muestras es un diseño de estudio muy potente. Pasa por alto muchas fuentes no deseadas de “ruido estadístico” que de otro modo podrían influir en el resultado del experimento, y se centra en la posible diferencia que podría surgir del único factor de interés.
Si la muestra es grande (lo que significa que\(n\geq 30\)) entonces en la fórmula para el intervalo de confianza podemos reemplazar\(t_{\alpha /2}\) por\(z_{\alpha /2}\). Para las pruebas de hipótesis cuando el número de pares es al menos\(30\), podemos usar el mismo estadístico que para las muestras pequeñas para las pruebas de hipótesis, excepto que ahora sigue una distribución normal estándar, por lo que usamos la última línea de la Figura 7.1.6 para calcular valores críticos, y\(p\) -valores pueden calcularse exactamente con la Figura 7.1.5, no meramente estimada usando la Figura 7.1.6.
Llave para llevar
- Cuando los datos se recogen en pares, las diferencias calculadas para cada par son los datos que se utilizan en las fórmulas.
- Un intervalo de confianza para la diferencia en dos medias poblacionales mediante muestreo pareado se computa usando una fórmula de la misma manera que se hizo para una sola media poblacional.
- El mismo procedimiento de cinco pasos utilizado para probar hipótesis relativas a una media de una sola población se utiliza para probar hipótesis sobre la diferencia entre dos medias poblacionales usando muestreo por pares. La única diferencia está en la fórmula para el estadístico de prueba estandarizado.

