27.3: Ejemplos de Ajuste de Modelo Problemático

Digamos que había otra variable en juego en este conjunto de datos, de la que no estábamos al tanto. Esta variable hace que algunos de los casos tengan valores mucho mayores que otros, de una manera que no está relacionada con la variable X. Jugamos un truco aquí usando la función seq () para crear una secuencia de cero a uno, y luego umbral esos 0.5 (para obtener la mitad de los valores como cero y la otra mitad como uno) y luego multiplicar por el tamaño del efecto deseado:

effsize=2
regression_data <- regression_data %>%
  mutate(y2=y + effsize*(seq(1/npoints,1,1/npoints)>0.5))

lm_result2 <- lm(y2 ~ x, data=regression_data)
summary(lm_result2)

## 
## Call:
## lm(formula = y2 ~ x, data = regression_data)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -2.3324 -0.9689 -0.0939  1.0421  2.2591 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   10.978      0.117   93.65   <2e-16 ***
## x              0.270      0.119    2.27    0.025 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.2 on 98 degrees of freedom
## Multiple R-squared:  0.0501, Adjusted R-squared:  0.0404 
## F-statistic: 5.17 on 1 and 98 DF,  p-value: 0.0252

Una cosa que debes notar es que el modelo ahora encaja en general mucho peor; el R-cuadrado es aproximadamente la mitad de lo que era en el modelo anterior, lo que refleja el hecho de que se agregó más variabilidad a los datos, pero no se contabilizó en el modelo. Veamos si nuestros informes de diagnóstico nos pueden dar alguna idea:

autoplot(lm_result2,which=1:2)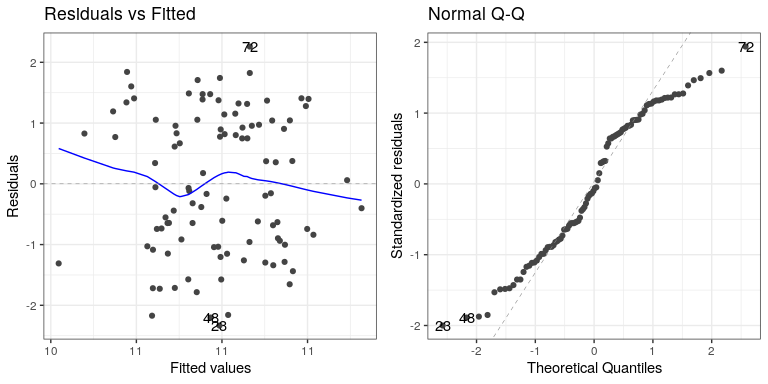

El gráfico residual versus ajustado no nos da mucha idea, pero vemos en la gráfica Q-Q que los residuos están divergiendo bastante de la línea unitaria.

Veamos otro problema potencial, en el que la variable y está relacionada de manera no lineal con la variable X. Podemos crear estos datos al cuadrar la variable X cuando generamos la variable Y:

effsize=2
regression_data <- regression_data %>%
  mutate(y3 = (x**2)*slope + rnorm(npoints)*noise_sd + intercept)

lm_result3 <- lm(y3 ~ x, data=regression_data)
summary(lm_result3)

## 
## Call:
## lm(formula = y3 ~ x, data = regression_data)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -1.610 -0.568 -0.065  0.359  3.266 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  10.5547     0.0844  125.07   <2e-16 ***
## x            -0.0419     0.0854   -0.49     0.62    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.84 on 98 degrees of freedom
## Multiple R-squared:  0.00245,    Adjusted R-squared:  -0.00773 
## F-statistic: 0.241 on 1 and 98 DF,  p-value: 0.625

Ahora vemos que no existe una relación lineal significativa entre$X$y Y/ Pero si miramos los residuales el problema con el modelo queda claro:

autoplot(lm_result3,which=1:2)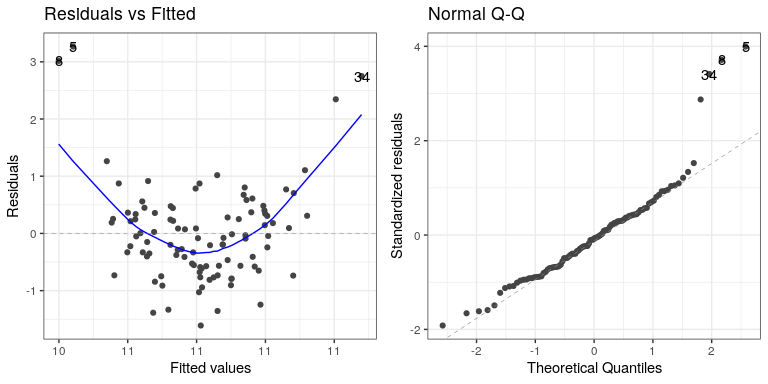

En este caso podemos ver la relación claramente no lineal entre los valores predichos y residuales, así como la clara falta de normalidad en los residuales.

Como señalamos en el capítulo anterior, el “lineal” en el modelo lineal general no se refiere a la forma de la respuesta, sino que se refiere al hecho de que el modelo es lineal en sus parámetros, es decir, los predictores en el modelo solo se multiplican los parámetros (e.g., en lugar de elevarse a una potencia de el parámetro). Así es como construiríamos un modelo que pudiera dar cuenta de la relación no lineal:

# create x^2 variable
regression_data <- regression_data %>%
  mutate(x_squared = x**2)

lm_result4 <- lm(y3 ~ x + x_squared, data=regression_data)
summary(lm_result4)

## 
## Call:
## lm(formula = y3 ~ x + x_squared, data = regression_data)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.4101 -0.3791 -0.0048  0.3908  1.4437 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  10.1087     0.0739   136.8   <2e-16 ***
## x            -0.0118     0.0600    -0.2     0.84    
## x_squared     0.4557     0.0451    10.1   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.59 on 97 degrees of freedom
## Multiple R-squared:  0.514,  Adjusted R-squared:  0.504 
## F-statistic: 51.2 on 2 and 97 DF,  p-value: 6.54e-16

Ahora vemos que el efecto de$X$es significativo, y si miramos la trama residual deberíamos ver que las cosas se ven mucho mejor:

autoplot(lm_result4,which=1:2)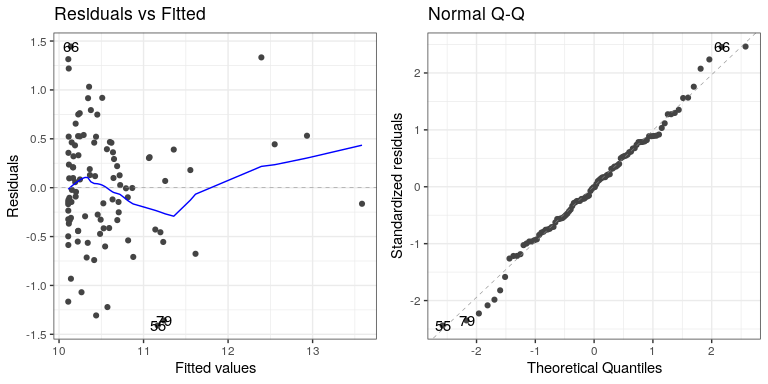

No perfecto, ¡pero mucho mejor que antes!