3.5: Distribuciones condicionales
- Page ID
- 151594
En esta sección, estudiamos cómo cambia una distribución de probabilidad cuando una variable aleatoria dada tiene un valor especificado conocido. Por lo que este es un tema esencial que trata sobre las medidas de probabilidad hou deben actualizarse a la luz de la nueva información. Como de costumbre, si eres un estudiante nuevo o probabilidad, es posible que quieras saltarte los detalles técnicos.
Teoría Básica
Nuestro punto de partida es un experimento aleatorio modelado por un espacio de probabilidad\((\Omega, \mathscr F, \P)\). Entonces, para revisar,\(\Omega\) es el conjunto de resultados,\(\mathscr F\) es la colección de eventos, y\(\P\) es la medida de probabilidad en el espacio muestral subyacente\((\Omega, \mathscr F)\).
Supongamos que\(X\) es una variable aleatoria definida en el espacio muestral (es decir, definida para el experimento), tomando valores en un conjunto\(S\).
Detalles
Técnicamente, la colección de eventos\(\mathscr F\) es un\(\sigma\) álgebra, por lo que el espacio muestral\((\Omega, \mathscr F)\) es un espacio medible. De igual manera,\(S\) tendrá una\(\sigma\) -álgebra de subconjuntos admisibles, por lo que también\((S, \mathscr S)\) es un espacio medible. \(X\)La variable aleatoria es medible, de modo que\(\{X \in A\} \in \mathscr F\) para cada\(A \in \mathscr S\). La distribución de\(X\) es la medida de probabilidad\(A \mapsto \P(X \in A)\) para\(A \in \mathscr S\).
El propósito de esta sección es estudiar la medida de probabilidad condicional dada\(X = x\) para\(x \in S\). Es decir, si\(E\) es un evento, nos gustaría definir y estudiar la probabilidad de\(E\) dado\(X = x\), denotado\(\P(E \mid X = x)\). Si\(X\) tiene una distribución discreta, el evento condicionamiento tiene probabilidad positiva, por lo que no se involucran nuevos conceptos, y la simple definición de probabilidad condicional es suficiente. Cuando\(X\) tiene una distribución continua, sin embargo, el evento condicionamiento tiene probabilidad 0, por lo que se necesita un enfoque fundamentalmente nuevo.
El caso discreto
Supongamos primero que\(X\) tiene una distribución discreta con función de densidad de probabilidad\(g\). Así\(S\) es contable y podemos suponer que\(g(x) = \P(X = x) \gt 0\) para\(x \in S\).
Si\(E\) es un evento y\(x \in S\) luego\[\P(E \mid X = x) = \frac{\P(E, X = x)}{g(x)}\]
Prueba
El significado de distribución discreta es que\(S\) es contable y\(\mathscr S = \mathscr P(S)\) es la colección de todos los subconjuntos de\(S\). Técnicamente,\(g\) es la función de densidad de probabilidad de\(X\) con respct a medida\(\#\) de conteo\(S\), la medida estándar para espacios discretos. En la ecuación diplay anterior, la coma que separa los eventos en el numerador de la fracción significa y, y así funciona igual que el símbolo de intersección. Este resultado se desprende inmediatamente de la definición de probabilidad condicional:\[ \P(E \mid X = x) = \frac{\P(E, X = x)}{\P(X = x)} = \frac{\P(E, X = x)}{g(x)} \]
El siguiente resultado es un caso sepcial de la ley de probabilidad total. y será la clave de la definición cuando\(X\) tenga una distribución continua.
Si\(E\) es un evento entonces\[\P(E, X \in A) = \sum_{x \in A} g(x) \P(E \mid X = x), \quad A \subseteq S\] Por el contrario, esta condición determina de manera única\(\P(E \mid X = x)\).
Prueba
Como se señaló, la ecuación mostrada es solo un caso especial de la ley de probabilidad total. Para\(A \subseteq S\), la colección contable de\( \left\{\{X = x\}: x \in A\right\} \) particiones de eventos\( \{X \in A\} \) así\[ \P(E, X \in A) = \sum_{x \in A} \P(E, X = x) = \sum_{x \in A} \P(E \mid X = x) \P(X = x) = \sum_{x \in A} \P(E \mid X = x) g(x) \] Por el contrario, supongamos que la función\(Q(x, E)\), definida para\(x \in S\) y\(E \in \mathscr F\), satisface\[\P(E, X \in A) = \sum_{x \in A} g(x) Q(x, E), \quad A \subseteq S\] Dejar\(A = \{x\}\) para\(x \in S\) da\(\P(E, X = x) = g(x) Q(x, E)\), así\(Q(x, E) = \P(E, X = x) \big/ g(x) = \P(E \mid X = x)\).
El Caso Continuo
Supongamos ahora que\(X\) tiene una distribución continua encendida\(S \subseteq \R^n\) para algunos\(n \in \N_+\), con función de densidad de probabilidad\(g\). Asumimos que\(g(x) \gt 0\) para\(x \in S\). A diferencia del caso discreto, no podemos usar probabilidad condicional simple para definir\(\P(E \mid X = x)\) para un evento\(E\) y\(x \in S\) porque el evento condicionamiento tiene probabilidad 0. No obstante, el concepto debería tener sentido. Si realmente ejecutamos el experimento,\(X\) tomará algún valor\(x\) (aunque a priori, este evento ocurre con probabilidad 0), y seguramente la información que en general\(X = x\) debería alterar las probabilidades que asignamos a otros eventos. Un enfoque natural es utilizar los resultados obtenidos en el caso discreto como definiciones en el caso continuo.
Si\(E\) es un evento y\(x \in S\), la probabilidad condicional\(\P(E \mid X = x)\) se define por el requisito de que\[\ \P(E, X \in A) = \int_A g(x) \P(E \mid X = x) \, dx, \quad A \subseteq S \]
Detalles
Técnicamente,\(S\) es un subconjunto medible de\(\R^n\) y la\(\sigma\) -álgebra\(\mathscr S\) consiste en los subconjuntos de\(S\) que también son medibles como subconjuntos de\(\R^n\). También\(g\) se requiere que la función sea medible, y es la función de densidad\(X\) con respecto a la medida de Lebesgue\(\lambda_n\). La medida de Lebesgue se llama así por Henri Lebesgue y es la medida estándar en\(\R^n\).
Aceptaremos el hecho de que se\(\P(E \mid X = x)\) pueda definir de manera única, hasta un conjunto de medida 0, por la condición anterior, pero volveremos a este punto en el apartado de Expectativa Condicional en el capítulo sobre Valor Esperado. Esencialmente la condición significa que\(\P(E \mid X = x)\) se define de manera que\(x \mapsto g(x) \P(E \mid X = x)\) es una función de densidad para la medida finita\(A \mapsto \P(E, X \in A)\).
Acondicionamiento y teorema de Bayes
Supongamos nuevamente que\(X\) es una variable aleatoria con valores en\(S\) y función de densidad de probabilidad\(g\), como se describió anteriormente. Nuestras discusiones anteriores en los casos discretos y continuos conducen a fórmulas básicas para computar la probabilidad de un evento condicionando\(X\).
La ley de probabilidad total. Si\(E\) es un evento, entonces se\(\P(E)\) puede calcular de la siguiente manera:
- Si X tiene una distribución discreta entonces\[\P(E) = \sum_{x \in S} g(x) \P(E \mid X = x) \]
- Si X tiene una distribución continua entonces\[\P(E) = \int_S g(x) \P(E \mid X = x) \, dx\]
Prueba
- Esto se desprende del teorema discreto con\(A = S\).
- Esto se desprende de la definición fundamental con\(A = S\).
Naturalmente, la ley de probabilidad total es útil cuando\(\P(E \mid X = x)\) y\(g(x)\) son conocidos por\(x \in S\). Nuestro siguiente resultado es, el Teorema de Bayes, que lleva el nombre de Thomas Bayes.
Teorema de Bayes. Supongamos que\(E\) es un evento con\(\P(E) \gt 0\). La función de densidad de probabilidad condicional\(x \mapsto g(x \mid E)\) de\(X\) dada se\(E\) puede calcular de la siguiente manera:
- Si\(X\) tiene una distribución discreta entonces\[g(x \mid E) = \frac{g(x) \P(E \mid X = x)}{\sum_{s \in S} g(s) \P(E \mid X = s)}, \quad x \in S \]
- Si\(X\) tiene una distribución continua entonces\[g(x \mid E) = \frac{g(x) \P(E \mid X = x)}{\int_S g(s) \P(E \mid X = s) \, ds}, \quad x \in S\]
Prueba
- En el caso discreto, como es habitual, basta con la definición simple ordinaria de probabilidad condicional. El numerador en la ecuación mostrada es\(\P(X = x) \P(E \mid X = x) = \P(E, X = x)\). El denominador es\(\P(E)\) por la parte (a) de la ley de probabilidad total. De ahí que la fracción sea\(\P(E, X = x) / \P(E) = \P(X = x \mid E)\).
- En el caso continuo, como es habitual, el argumento es más sutil. Necesitamos mostrar que la expresión en la ecuación mostrada satisface la propiedad definitoria de un PDF para la distribución conditinal. Una vez más, el denominador es\(\P(E)\) por la parte (b) de la ley de probabilidad total. Si\( A \subseteq S \) entonces usando la definición fundamental,\[ \int_A g(x \mid E) \, dx = \frac{1}{\P(E)} \int_A g(x) \P(E \mid X = x) \, dx = \frac{\P(E, X \in A)}{\P(E)} = \P(X \in A \mid E) \] Por el sentido del término,\(x \mapsto g(x \mid E) \) es la función de densidad de probabilidad condicional de\( X \) dado\( E \).
En el contexto del teorema de\(g\) Bayes, se llama la función de densidad de probabilidad previa de\(X\) y\(x \mapsto g(x \mid E)\) es la función de densidad de probabilidad posterior de\(X\) dado\(E\). Obsérvese también que la función de densidad de probabilidad condicional de\(X\) dado\(E\) es proporcional a la función\(x \mapsto g(x) \P(E \mid X = x)\), la suma o integral de esta función que ocurre en el denominador es simplemente la constante normalizadora. Al igual que con la ley de probabilidad total, el teorema de Bayes es útil cuando\(\P(E \mid X = x)\) y\(g(x)\) son conocidos por\(x \in S\).
Funciones de densidad de probabilidad condicional
Las definiciones y resultados anteriores se aplican, por supuesto, si\(E\) es un evento definido en términos de otra variable aleatoria para nuestro experimento. Aquí está la configuración:
Supongamos que\(X\) y\(Y\) son variables aleatorias en el espacio de probabilidad, con valores en conjuntos\(S\) y\(T\), respectivamente, por lo que\((X, Y)\) es una variable aleatoria con valores en\(S \times T\). Suponemos que\((X, Y)\) tiene función de densidad de probabilidad\(f\), como se discute en la sección sobre Distribuciones Conjuntas. Recuerde que\(X\) tiene la función de densidad de probabilidad\(g\) definida de la siguiente manera:
- Si\(Y\) tiene una distribución discreta en el conjunto contable\(T\), entonces\[g(x) = \sum_{y \in T} f(x, y), \quad x \in S\]
- Si\(Y\) tiene una distribución continua en\(T \subseteq \R^k\) entonces\[g(x) = \int_T f(x, y) dy, \quad x \in S\]
Similarmente, la función\( h \) de densidad de probabilidad de se\( Y \) puede obtener sumando\( f \)\(x \in S\) si\(X\) tiene una distribución discreta o integrando\(f\) sobre\(S\) si\(X\) tiene una distribución continua.
Supongamos eso\( x \in S \) y aquello\( g(x) \gt 0 \). La función\( y \mapsto h(y \mid x) \) definida a continuación es una función de densidad de probabilidad en\( T \):\[h(y \mid x) = \frac{f(x, y)}{g(x)}, \quad y \in T\]
Prueba
El resultado es sencillo, ya que\( g(x) \) es la constante normalizadora para\( y \mapsto h(y \mid x) \). Específicamente, arreglar\( x \in S \). Entonces\( h(y \mid x) \ge 0 \). Si\(Y\) tiene una distribución discreta entonces\[ \sum_{y \in T} h(y \mid x) = \frac{1}{g(x)} \sum_{y \in T} f(x, y) = \frac{g(x)}{g(x)} = 1\] Similarmente, si\(Y\) tiene una distribución continua entonces\[ \int_T h(y \mid x) \, dy = \frac{1}{g(x)} \int_T f(x, y) \, dy = \frac{g(x)}{g(x)} = 1\]
La distribución que corresponde a esta función de densidad de probabilidad es lo que esperarías:
Para\(x \in S\), la función\(y \mapsto h(y \mid x)\) es la función de densidad de probabilidad condicional de\(Y\) dado\(X = x\). Es decir,
- Si\(Y\) tiene una distribución discreta entonces\[\P(Y \in B \mid X = x) = \sum_{y \in B} h(y \mid x), \quad B \subseteq T\]
- Si\(Y\) tiene una distribución continua entonces\[\P(Y \in B \mid X = x) = \int_B h(y \mid x) \, dy, \quad B \subseteq T\]
Prueba
Hay cuatro casos, dependiendo del tipo de distribución de\(X\) y\(Y\), pero los cálculos son idénticos, excepto las sumas en el caso discreto y las integrales en el caso continuo. La herramienta principal es el teorema básico cuando\(X\) tiene una distribución discreta y la definición fundamental cuando\(X\) tiene una distribución continua, con el evento\(E\) reemplazado por\(\{Y \in B\}\) for\(B \subseteq T\). El otro elemento principal es el hecho de que\(f\) es el PDF de la distribución (conjunta) de\((X, Y)\).
- Supongamos que\(Y\) tiene una distribución discreta en el conjunto contable\(T\). Si\(X\) también tiene una distribución discreta en el conjunto contable\(S\) entonces\[ \sum_{x \in A} g(x) \sum_{y \in B} h(y \mid x) = \sum_{x \in A} \sum_{y \in B} g(x) h(y \mid x) = \sum_{x \in A} \sum_{y \in B} f(x, y) = \P(X \in A, Y \in B), \quad A \subseteq S \] En este caso discreto conjuntamente, hay un argumento más simple, por supuesto:\[h(y \mid x) = \frac{f(x, y)}{g(x)} = \frac{\P(X = x, Y = y)}{P(X = x)} = \P(Y = y \mid X = x), \quad y \in T\] Si\(X\) tiene una distribución continua en\(S \subseteq \R^j\) entonces\[ \int_A g(x) \sum_{y \in B} h(y \mid x) \, dx = \int_A \sum_{y \in B} g(x) h(y \mid x) \, dx = \int_A \sum_{y \in B} f(x, y) = \P(X \in A, Y \in B), \quad A \subseteq S \]
- Supongamos que\(Y\) tiene distribuciones continuas en\(T \subseteq \R^k\). Si\(X\) tiene una distribución discreta en el conjunto contable\(S\), entonces\[ \sum_{x \in A} g(x) \int_B h(y \mid x) \, dy = \sum_{x \in A} \int_B g(x) h(y \mid x) \, dy = \sum_{x \in A} \int_B f(x, y) \, dy = \P(X \in A, Y \in B), \quad A \subseteq S \] Si\(X\) tiene una distribución continua\(S \subseteq \R^j\), entonces\[ \int_A g(x) \int_B h(y \mid x) \, dy \, dx = \int_A \int_B g(x) h(y \mid x) \, dy \, dx = \int_A \int_B f(x, y) \, dy \, dx = \P(X \in A, Y \in B), \quad A \subseteq S \]
El siguiente teorema da el teorema de Bayes para funciones de densidad de probabilidad. Utilizamos la notación establecida anteriormente.
Teorema de Bayes. Para\(y \in T\), la función de densidad de probabilidad condicional\(x \mapsto g(x \mid y)\) de\(X\) dado se\(y = y\) puede calcular de la siguiente manera:
- Si\(X\) tiene una distribución discreta entonces\[g(x \mid y) = \frac{g(x) h(y \mid x)}{\sum_{s \in S} g(s) h(y \mid s)}, \quad x \in S\]
- Si\(X\) tiene una distribución continua entonces\[g(x \mid y) = \frac{g(x) h(y \mid x)}{\int_S g(s) h(y \mid s) ds}, \quad x \in S\]
Prueba
En ambos casos el numerador está\( f(x, y) \) mientras que el denominador es\(h(y)\).
En el contexto del teorema de\(g\) Bayes, es la función de densidad de probabilidad previa de\(X\) y\(x \mapsto g(x \mid y)\) es la función de densidad de probabilidad posterior de\(X\) dada\(Y = y\) para\(y \in T\). Tenga en cuenta que la función de densidad de probabilidad posterior\(x \mapsto g(x \mid y)\) es proporcional a la función\(x \mapsto g(x) h(y \mid x)\). La suma o integral en el denominador es la constante normalizadora.
Independencia
Intuitivamente,\(X\) y\(Y\) debe ser independiente si y sólo si las distribuciones condicionales son las mismas que las distribuciones incondicionales correspondientes.
Las siguientes condiciones son equivalentes:
- \(X\)y\(Y\) son independientes.
- \(f(x, y) = g(x) h(y)\)para\(x \in S\),\(y \in T\)
- \(h(y \mid x) = h(y)\)para\(x \in S\),\(y \in T\)
- \(g(x \mid y) = g(x)\)para\(x \in S\),\(y \in T\)
Prueba
La equivalencia de (a) y (b) se estableció en la sección sobre distribuciones conjuntas. Las partes (c) y (d) son equivalentes a (b). Para una distribución continua como se describe en los detalles en (4), una función de densidad de probabilidad no es única. Los valores de un PDF se pueden cambiar a otros valores no negativos en un conjunto de medida 0 y la función resultante sigue siendo un PDF. Entonces, si\(X\) o\(Y\) tiene una distribución continua, las ecuaciones anteriores tienen que ser interpretadas como mantenidas para\(x\) o\(y\), respectivamente, excepto en un conjunto de medida 0.
Ejemplos y Aplicaciones
En los ejercicios que siguen, busca modelos y distribuciones especiales que hemos estudiado. Una distribución especial puede estar incrustada en un problema mayor, como una distribución condicional, por ejemplo. En particular, a veces surge una distribución condicional cuando se aleatoriza un parámetro de una distribución estándar.
Un par de distribuciones especiales ocurrirán frecuentemente en los ejercicios. Primero, recordemos que la distribución uniforme discreta en un conjunto finito y no vacío\(S\) tiene la función de densidad de probabilidad\(f\) dada por\(f(x) = 1 \big/ \#(S)\) for\(x \in S\). Esta distribución gobierna un elemento seleccionado al azar de\(S\).
Recordemos también que los ensayos de Bernoulli (llamados así por Jacob Bernoulli) son ensayos independientes, cada uno con dos posibles resultados genéricamente llamados éxito y fracaso. La probabilidad de éxito\(p \in [0, 1]\) es la misma para cada ensayo, y es el parámetro básico del proceso aleatorio. El número de éxitos en los ensayos de\(n \in \N_+\) Bernoulli tiene la distribución binomial con parámetros\(n\) y\(p\). Esta distribución tiene función de densidad de probabilidad\(f\) dada por\(f(x) = \binom{n}{x} p^x (1 - p)^{n - x}\) for\(x \in \{0, 1, \ldots, n\}\). La distribución binomial se estudia con más detalle en el capítulo sobre los ensayos de Bernoulli
Monedas y dados
Supongamos que se lanzan dos dados estándar y justos y\((X_1, X_2)\) se registra la secuencia de puntuaciones. Dejar\(U = \min\{X_1, X_2\}\) y\(V = \max\{X_1, X_2\}\) denotar las puntuaciones mínimas y máximas, respectivamente.
- Encuentra la función de densidad de probabilidad condicional de\(U\) dada\(V = v\) para cada uno\(v \in \{1, 2, 3, 4, 5, 6\}\).
- Encuentra la función de densidad de probabilidad condicional de\(V\) dada\(U = u\) para cada uno\(u \in \{1, 2, 3, 4, 5, 6\}\).
Contestar
-
\(g(u \mid v)\) \(u = 1\) 2 3 4 5 6 \(v = 1\) 1 0 0 0 0 0 2 \(\frac{2}{3}\) \(\frac{1}{3}\) 0 0 0 0 3 \(\frac{2}{5}\) \(\frac{2}{5}\) \(\frac{1}{5}\) 0 0 0 4 \(\frac{2}{7}\) \(\frac{2}{7}\) \(\frac{2}{7}\) \(\frac{1}{7}\) 0 0 5 \(\frac{2}{9}\) \(\frac{2}{9}\) \(\frac{2}{9}\) \(\frac{2}{9}\) \(\frac{1}{9}\) 0 6 \(\frac{2}{11}\) \(\frac{2}{11}\) \(\frac{2}{11}\) \(\frac{2}{11}\) \(\frac{2}{11}\) \(\frac{1}{11}\) -
\(h(v \mid u)\) \(u = 1\) 2 3 4 5 6 \(v = 1\) \(\frac{1}{11}\) 0 0 0 0 0 2 \(\frac{2}{11}\) \(\frac{1}{9}\) 0 0 0 0 3 \(\frac{2}{11}\) \(\frac{2}{9}\) \(\frac{1}{7}\) 0 0 0 4 \(\frac{2}{11}\) \(\frac{2}{9}\) \(\frac{2}{7}\) \(\frac{1}{5}\) 0 0 5 \(\frac{2}{11}\) \(\frac{2}{9}\) \(\frac{2}{7}\) \(\frac{2}{5}\) \(\frac{1}{3}\) 0 6 \(\frac{2}{11}\) \(\frac{2}{9}\) \(\frac{2}{7}\) \(\frac{2}{5}\) \(\frac{2}{3}\) \(1\)
En el experimento de la troquela-moneda, se enrolla un dado estándar justo y luego se lanza una moneda justa el número de veces que se muestra en el dado. Dejar\(N\) denotar la puntuación del dado y\(Y\) el número de cabezas.
- Encuentra la función de densidad de probabilidad conjunta de\((N, Y)\).
- Encuentra la función de densidad de probabilidad de\(Y\).
- Encuentra la función de densidad de probabilidad condicional de\(N\) dada\(Y = y\) para cada uno\(y \in \{0, 1, 2, 3, 4, 5, 6\}\).
Contestar
- y b.
\(f(n, y)\) \(n = 1\) 2 3 4 5 6 \(h(y)\) \(y = 0\) \(\frac{1}{12}\) \(\frac{1}{24}\) \(\frac{1}{48}\) \(\frac{1}{96}\) \(\frac{1}{102}\) \(\frac{1}{384}\) \(\frac{63}{384}\) 1 \(\frac{1}{12}\) \(\frac{1}{12}\) \(\frac{1}{16}\) \(\frac{1}{24}\) \(\frac{5}{192}\) \(\frac{1}{64}\) \(\frac{120}{384}\) 2 0 \(\frac{1}{24}\) \(\frac{1}{16}\) \(\frac{1}{16}\) \(\frac{5}{96}\) \(\frac{5}{128}\) \(\frac{99}{384}\) 3 0 0 \(\frac{1}{48}\) \(\frac{1}{24}\) \(\frac{5}{96}\) \(\frac{5}{96}\) \(\frac{64}{384}\) 4 0 0 0 \(\frac{1}{96}\) \(\frac{5}{192}\) \(\frac{5}{128}\) \(\frac{29}{384}\) 5 0 0 0 0 \(\frac{1}{192}\) \(\frac{1}{64}\) \(\frac{8}{384}\) 6 0 0 0 0 0 \(\frac{1}{384}\) \(\frac{1}{384}\) \(g(n)\) \(\frac{1}{6}\) \(\frac{1}{6}\) \(\frac{1}{6}\) \(\frac{1}{6}\) \(\frac{1}{6}\) \(\frac{1}{6}\) 1 -
\(g(n \mid y)\) \(n = 1\) 2 3 4 5 6 \(y = 0\) \(\frac{32}{63}\) \(\frac{16}{63}\) \(\frac{8}{63}\) \(\frac{4}{63}\) \(\frac{2}{63}\) \(\frac{1}{63}\) 1 \(\frac{16}{60}\) \(\frac{16}{60}\) \(\frac{12}{60}\) \(\frac{8}{60}\) \(\frac{5}{60}\) \(\frac{3}{60}\) 2 0 \(\frac{16}{99}\) \(\frac{24}{99}\) \(\frac{24}{99}\) \(\frac{20}{99}\) \(\frac{15}{99}\) 3 0 0 \(\frac{2}{16}\) \(\frac{4}{16}\) \(\frac{5}{16}\) \(\frac{5}{16}\) 4 0 0 0 \(\frac{4}{29}\) \(\frac{10}{29}\) \(\frac{15}{29}\) 5 0 0 0 0 \(\frac{1}{4}\) \(\frac{3}{4}\) 6 0 0 0 0 0 1
En el experimento de die-coin, seleccione el dado justo y la moneda.
- Ejecutar la simulación de 1000 veces y comparar la función de densidad empírica de\(Y\) con la función de densidad de probabilidad verdadera en el ejercicio anterior
- Ejecutar la simulación 1000 veces y calcular la función de densidad condicional empírica de\(N\) dado\(Y = 3\). Comparar con las funciones de densidad de probabilidad condicional en el ejercicio anterior.
En el experimento de troqueles, se arroja una moneda justa. Si la moneda es colas, se enrolla una matriz estándar y justa. Si la moneda es cabezas, se enrolla una matriz plana estándar, ace-seis (las caras 1 y 6 tienen probabilidad\(\frac{1}{4}\) cada una y las caras 2, 3, 4, 5 tienen probabilidad\(\frac{1}{8}\) cada una). Dejar\(X\) denotar la puntuación de la moneda (0 para las colas y 1 para las cabezas) y\(Y\) la puntuación del dado.
- Encuentra la función de densidad de probabilidad conjunta de\((X, Y)\).
- Encuentra la función de densidad de probabilidad de\(Y\).
- Encuentra la función de densidad de probabilidad condicional de\(X\) dada\(Y = y\) para cada uno\(y \in \{1, 2, 3, 4, 5, 6\}\).
Contestar
- y b.
\(f(x, y)\) \(y = 1\) 2 3 4 5 6 \(g(x)\) \(x = 0\) \(\frac{1}{12}\) \(\frac{1}{12}\) \(\frac{1}{12}\) \(\frac{1}{12}\) \(\frac{1}{12}\) \(\frac{1}{12}\) \(\frac{1}{2}\) 1 \(\frac{1}{8}\) \(\frac{1}{16}\) \(\frac{1}{16}\) \(\frac{1}{16}\) \(\frac{1}{16}\) \(\frac{1}{8}\) \(\frac{1}{2}\) \(h(y)\) \(\frac{5}{24}\) \(\frac{7}{24}\) \(\frac{7}{48}\) \(\frac{7}{48}\) \(\frac{7}{48}\) \(\frac{5}{24}\) 1 -
\(g(x \mid y)\) \(y = 1\) 2 3 4 5 6 \(x = 0\) \(\frac{2}{5}\) \(\frac{4}{7}\) \(\frac{4}{7}\) \(\frac{4}{7}\) \(\frac{4}{7}\) \(\frac{2}{5}\) 1 \(\frac{3}{5}\) \(\frac{3}{7}\) \(\frac{3}{7}\) \(\frac{3}{7}\) \(\frac{3}{7}\) \(\frac{3}{5}\)
En el experimento de monedas-dado, seleccione los ajustes del ejercicio anterior.
- Ejecute la simulación 1000 veces y compare la función de densidad empírica de\(Y\) con la función de densidad de probabilidad verdadera en el ejercicio anterior.
- Ejecutar la simulación 100 veces y calcular la función empírica de densidad de probabilidad condicional de\(X\) dado\(Y = 2\). Comparar con la función de densidad de probabilidad condicional en el ejercicio anterior.
Supongamos que una caja contiene 12 monedas: 5 son justas, 4 están sesgadas para que las cabezas surjan probabilidad\(\frac{1}{3}\), y 3 son de dos cabezas. Una moneda se elige al azar y se arroja 2 veces. Dejar\(P\) denotar la probabilidad de cabezas de la moneda seleccionada, y\(X\) el número de cabezas.
- Encuentra la función de densidad de probabilidad conjunta de\((P, X)\).
- Encuentra la función de densidad de probabilidad de\(X\).
- Encuentra la función de densidad de probabilidad condicional de\(P\) dado\(X = x\) para\(x \in \{0, 1, 2\}\).
Contestar
- y b.
\(f(p, x)\) \(x = 0\) 1 2 \(g(p)\) \(p = \frac{1}{2}\) \(\frac{5}{48}\) \(\frac{10}{48}\) \(\frac{5}{48}\) \(\frac{5}{12}\) \(\frac{1}{3}\) \(\frac{4}{27}\) \(\frac{4}{27}\) \(\frac{1}{27}\) \(\frac{4}{12}\) 1 0 0 \(\frac{1}{4}\) \(\frac{3}{12}\) \(h(x)\) \(\frac{109}{432}\) \(\frac{154}{432}\) \(\frac{169}{432}\) 1 -
\(g(p \mid x)\) \(x = 0\) 1 2 \(p = \frac{1}{2}\) \(\frac{45}{109}\) \(\frac{45}{77}\) \(\frac{45}{169}\) \(\frac{1}{3}\) \(\frac{64}{109}\) \(\frac{32}{77}\) \(\frac{16}{169}\) 1 0 0 \(\frac{108}{169}\)
Compara el experimento de troquelado con el experimento de caja de monedas. En el primer experimento, arrojamos una moneda con una probabilidad fija de cabezas un número aleatorio de veces. En el segundo experimento, efectivamente arrojamos una moneda con una probabilidad aleatoria de cabezas un número fijo de veces.
Supongamos que\(P\) tiene función de densidad de probabilidad\(g(p) = 6 p (1 - p)\) para\(p \in [0, 1]\). Dado\(P = p\), una moneda con probabilidad de cabezas\(p\) es arrojado 3 veces. Vamos a\(X\) denotar el número de cabezas.
- Encuentra la función de densidad de probabilidad conjunta de\((P, X)\).
- Encuentra la densidad de probabilidad de función de\(X\).
- Encuentra la densidad de probabilidad condicional de\(P\) dado\(X = x\) para\(x \in \{0, 1, 2, 3\}\). Grafíquelas en los mismos ejes.
Contestar
- \(f(p, x) = 6 \binom{3}{x} p^{x+1}(1 - p)^{4-x}\)para\(p \in [0, 1]\) y\(x \in \{0, 1, 2, 3, 4\}\)
- \(h(0) = h(3) = \frac{1}{5}\),\(h(1) = h(2) = \frac{3}{10}\).
- \(g(p \mid 0) = 30 p (1 - p)^4\),\(g(p \mid 1) = 60 p^2 (1 - p)^3\),\(g(p \mid 2) = 60 p^3 (1 - p)^2\),\(g(p \mid 3) = 30 p^4 (1 - p)\), en cada caso para\(p \in [0, 1]\)
Compara el experimento de caja de monedas con el último experimento. En el segundo experimento, elegimos efectivamente una moneda de una caja con una infinidad continua de tipos de monedas. La distribución previa\(P\) y cada una de las distribuciones posteriores de\(P\) en la parte (c) son miembros de la familia de distribuciones beta, una de las razones de la importancia de la familia beta. Las distribuciones beta se estudian con más detalle en el capítulo sobre Distribuciones especiales.
En la simulación del experimento de monedas beta, establecer\( a = b = 2 \) y\( n = 3 \) obtener el experimento estudiado en el ejercicio anterior. Para varios valores verdaderos
de\( p \), ejecute el experimento en modo de un solo paso varias veces y observe la función de densidad de probabilidad posterior en cada ejecución.
Distribuciones Mixtas Simples
Recordemos que la distribución exponencial con parámetro de tasa\(r \in (0, \infty)\) tiene función de densidad de probabilidad\(f\) dada por\(f(t) = r e^{-r t}\) for\(t \in [0, \infty)\). La distribución exponencial se suele utilizar para modelar tiempos aleatorios, bajo ciertos supuestos. La distribución exponencial se estudia con más detalle en el capítulo sobre el Proceso de Poisson. Recordemos también que para\(a, \, b \in \R\) con\(a \lt b\), la distribución uniforme continua en el intervalo\([a, b]\) tiene función de densidad de probabilidad\(f\) dada por\(f(x) = \frac{1}{b - a}\) for\(x \in [a, b]\). Esta distribución gobierna un punto seleccionado al azar del intervalo.
Supongamos que hay 5 bombillas en una caja, etiquetadas del 1 al 5. La vida útil del bulbo\(n\) (en meses) tiene la distribución exponencial con parámetro de tasa\(n\). Se selecciona una bombilla al azar de la caja y se prueba.
- Encuentra la probabilidad de que la bombilla seleccionada dure más de un mes.
- Dado que la bombilla dura más de un mes, encuentra la función de densidad de probabilidad condicional del número de bombilla.
Contestar
Dejar\(N\) denotar el número de bombilla y\(T\) la vida útil.
- \(\P(T \gt 1) = 0.1156\)
-
\(n\) 1 2 3 4 5 \(g(n \mid T \gt 1)\) 0.6364 0.2341 0.0861 0.0317 0.0117
Supongamos que\(X\) se distribuye uniformemente en\(\{1, 2, 3\}\), y dado\(X = x \in \{1, 2, 3\}\), variable aleatoria\(Y\) se distribuye uniformemente en el intervalo\([0, x]\).
- Encuentra la función de densidad de probabilidad conjunta de\((X, Y)\).
- Encuentra la función de densidad de probabilidad de\(Y\).
- Encuentra la función de densidad de probabilidad condicional de\(X\) dado\(Y = y\) para\(y \in [0, 3]\).
Contestar
- \(f(x, y) = \frac{1}{3 x}\)para\(y \in [0, x]\) y\(x \in \{1, 2, 3\}\).
- \(h(y) = \begin{cases} \frac{11}{18}, & 0 \le y \le 1 \\ \frac{5}{18}, & 1 \lt y \le 2 \\ \frac{2}{18}, & 2 \lt y \le 3 \end{cases}\)
- Para\(y \in [0, 1]\),\(g(1 \mid y) = \frac{6}{11}\),\(g(2 \mid y) = \frac{3}{11}\),\(g(3 \mid y) = \frac{2}{11}\)
Para\(y \in (1, 2]\),\(g(1 \mid y) = 0\),\(g(2 \mid y) = \frac{3}{5}\),\(g(3 \mid y) = \frac{2}{5}\)
Para\(y \in (2, 3]\),\(g(1 \mid y) = g(2 \mid y) = 0\),\(g(3 \mid y) = 1\).
La distribución de Poisson
Recordemos que la distribución de Poisson con parámetro\(a \in (0, \infty)\) tiene función de densidad de probabilidad\(g(n) = e^{-a} \frac{a^n}{n!}\) para\(n \in \N\). Esta distribución es ampliamente utilizada para modelar el número de puntos aleatorios
en una región de tiempo o espacio; el parámetro\(a\) es proporcional al tamaño de la región. La distribución de Poisson lleva el nombre de Simeon Poisson, y se estudia con más detalle en el capítulo sobre el Proceso de Poisson.
Supongamos que\(N\) es el número de partículas elementales emitidas por una muestra de material radiactivo en un periodo de tiempo especificado, y tiene la distribución de Poisson con parámetro\(a\). Cada partícula emitida, independientemente de las otras, es detectada por un contador con probabilidad\(p \in (0, 1)\) y perdida con probabilidad\(1 - p\). Dejar\(Y\) denotar el número de partículas detectadas por el contador.
- Para\(n \in \N\), argumentar que la distribución condicional de\(Y\) dado\(N = n\) es binomial con parámetros\(n\) y\(p\).
- Encuentra la función de densidad de probabilidad conjunta de\((N, Y)\).
- Encuentra la función de densidad de probabilidad de\(Y\).
- Para\(y \in \N\), encontrar la función de densidad de probabilidad condicional de\(N\) dado\(Y = y\).
Contestar
- Cada partícula, independientemente, se detecta (éxito) con probabilidad\( p \). Esta es la definición misma de los ensayos de Bernoulli, así que dada\( N = n \), el número de partículas detectadas tiene la distribución binomial con parámetros\( n \) y\( p \)
- El PDF\(f\) de\((N, Y)\) está definido por\[f(n, y) = e^{-a} a^n \frac{p^y}{y!} \frac{(1-p)^{n-y}}{(n-y)!}, \quad n \in \N, \; y \in \{0, 1, \ldots, n\}\]
- El PDF\(h\) de\(Y\) se define por\[h(y) = e^{-p a} \frac{(p a)^y}{y!}, \quad y \in \N\] Esta es la distribución de Poisson con parámetro\(p a\).
- El PDF condicional de\(N\) dado\(Y = y\) se define por\[g(n \mid y) = e^{-(1-p)a} \frac{[(1 - p) a]^{n-y}}{(n - y)!}, \quad n \in \{y, y+1, \ldots\}\] Esta es la distribución de Poisson con parámetro\((1 - p)a\), desplazado para comenzar en\(y\).
El hecho de que\(Y\) también tenga una distribución de Poisson es una propiedad interesante y característica de la distribución. Esta propiedad se explora con más profundidad en la sección sobre adelgazamiento del proceso de Poisson.
Distribuciones continuas simples
Supongamos que\((X, Y)\) tiene la función de densidad de probabilidad\(f\) definida por\(f(x, y) = x + y\) for\((x, y) \in (0, 1)^2\).
- Encuentra la función de densidad de probabilidad condicional de\(X\) dada\(Y = y\) para\(y \in (0, 1)\)
- Encuentra la función de densidad de probabilidad condicional de\(Y\) dada\(X = x\) para\(x \in (0, 1)\)
- Encontrar\(\P\left(\frac{1}{4} \le Y \le \frac{3}{4} \bigm| X = \frac{1}{3}\right)\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- Para\(y \in (0, 1)\),\(g(x \mid y) = \frac{x + y}{y + 1/2}\) para\(x \in (0, 1)\)
- Para\(x \in (0, 1)\),\(h(y \mid x) = \frac{x + y}{x + 1/2}\) para\(y \in (0, 1)\)
- \(\frac{1}{2}\)
- \(X\)y\(Y\) son dependientes.
Supongamos que\((X, Y)\) tiene la función de densidad de probabilidad\(f\) definida por\(f(x, y) = 2 (x + y)\) for\(0 \lt x \lt y \lt 1\).
- Encuentra la función de densidad de probabilidad condicional de\(X\) dado\(Y = y\) para\(y \in (0, 1)\).
- Encuentra la función de densidad de probabilidad condicional de\(Y\) dado\(X = x\) para\(x \in (0, 1)\).
- Encontrar\(\P\left(Y \ge \frac{3}{4} \bigm| X = \frac{1}{2}\right)\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- Para\(y \in (0, 1)\),\(g(x \mid y) = \frac{x + y}{3 y^2}\) para\(x \in (0, y)\).
- Para\(x \in (0, 1)\),\(h(y \mid x) = \frac{x + y}{(1 + 3 x)(1 - x)}\) para\(y \in (x, 1)\).
- \(\frac{3}{10}\)
- \(X\)y\(Y\) son dependientes.
Supongamos que\((X, Y)\) tiene la función de densidad de probabilidad\(f\) definida por\(f(x, y) = 15 x^2 y\) for\(0 \lt x \lt y \lt 1\).
- Encuentra la función de densidad de probabilidad condicional de\(X\) dado\(Y = y\) para\(y \in (0, 1)\).
- Encuentra la función de densidad de probabilidad condicional de\(Y\) dado\(X = x\) para\(x \in (0, 1)\).
- Encontrar\(\P\left(X \le \frac{1}{4} \bigm| Y = \frac{1}{3}\right)\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- Para\(y \in (0, 1)\),\(g(x \mid y) = \frac{3 x^2}{y^3}\) para\(x \in (0, y)\).
- Para\(x \in (0, 1)\),\(h(y \mid x) = \frac{2 y}{1 - x^2}\) para\(y \in (x, 1)\).
- \(\frac{27}{64}\)
- \(X\)y\(Y\) son dependientes.
Supongamos que\((X, Y)\) tiene la función de densidad de probabilidad\(f\) definida por\(f(x, y) = 6 x^2 y\) for\(0 \lt x \lt 1\) y\(0 \lt y \lt 1\).
- Encuentra la función de densidad de probabilidad condicional de\(X\) dado\(Y = y\) para\(y \in (0, 1)\).
- Encuentra la función de densidad de probabilidad condicional de\(Y\) dado\(X = x\) para\(x \in (0, 1)\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- Para\(y \in (0, 1)\),\(g(x \mid y) = 3 x^2\) para\(y \in (0, 1)\).
- Para\(x \in (0, 1)\),\(h(y \mid x) = 2 y\) para\(y \in (0, 1)\).
- \(X\)y\(Y\) son independientes.
Supongamos que\((X, Y)\) tiene la función de densidad de probabilidad\(f\) definida por\(f(x, y) = 2 e^{-x} e^{-y}\) for\(0 \lt x \lt y \lt \infty\).
- Encuentra la función de densidad de probabilidad condicional de\(X\) dado\(Y = y\) para\(y \in (0, \infty)\).
- Encuentra la función de densidad de probabilidad condicional de\(Y\) dado\(X = x\) para\(x \in (0, \infty)\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- Para\(y \in (0, \infty)\),\(g(x \mid y) = \frac{e^{-x}}{1 - e^{-y}}\) para\(x \in (0, y)\).
- Para\(x \in (0, \infty)\),\(h(y \mid x) = e^{x-y}\) para\(y \in (x, \infty)\).
- \(X\)y\(Y\) son dependientes.
Supongamos que\(X\) se distribuye uniformemente en el intervalo\((0, 1)\), y eso dado\(X = x\),\(Y\) se distribuye uniformemente en el intervalo\((0, x)\).
- Encuentra la función de densidad de probabilidad conjunta de\((X, Y)\).
- Encuentra la función de densidad de probabilidad de\(Y\).
- Encuentra la función de densidad de probabilidad condicional de\(X\) dado\(Y = y\) para\(y \in (0, 1)\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- \(f(x, y) = \frac{1}{x}\)para\(0 \lt y \lt x \lt 1\)
- \(h(y) = -\ln y\)para\(y \in (0, 1)\)
- Para\(y \in (0, 1)\),\(g(x \mid y) = -\frac{1}{x \ln y}\) para\(x \in (y, 1)\).
- \(X\)y\(Y\) son dependientes.
Supongamos que\(X\) tiene la función de densidad de probabilidad\(g\) definida por\(g(x) = 3 x^2\) for\(x \in (0, 1)\). La función de densidad de probabilidad condicional de\(Y\) dado\(X = x\) es\(h(y \mid x) = \frac{3 y^2}{x^3}\) para\(y \in (0, x)\).
- Encuentra la función de densidad de probabilidad conjunta de\((X, Y)\).
- Encuentra la función de densidad de probabilidad de\(Y\).
- Encuentra la función de densidad de probabilidad condicional de\(X\) dado\(Y = y\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- \(f(x, y) = \frac{9 y^2}{x}\)para\(0 \lt y \lt x \lt 1\).
- \(h(y) = -9 y^2 \ln y\)para\(y \in (0, 1)\).
- Para\(y \in (0, 1)\),\(g(x \mid y) = - \frac{1}{x \ln y}\) para\(x \in (y, 1)\).
- \(X\)y\(Y\) son dependientes.
Distribuciones Uniformes Multivariadas
Las distribuciones uniformes multivariadas dan una interpretación geométrica de algunos de los conceptos de esta sección.
Recordemos que For\(n \in \N_+\), la medida estándar\(\lambda_n\) on\(\R^n\) viene dada por\[ \lambda_n(A) = \int_A 1 \, dx, \quad A \subseteq \R^n \] En particular,\(\lambda_1(A)\) es la longitud de\(A \subseteq \R\),\(\lambda_2(A)\) es el área de\(A \subseteq \R^2\) y\(\lambda_3(A)\) es el volumen de\(A \subseteq \R^3\).
Detalles
Técnicamente,\(\lambda_n\) es Lebesgue medida definida en el\(\sigma\) -álgebra de subconjuntos medibles de\(\R^n\). En la siguiente descripción, asumimos que todos los conjuntos son medibles. La representación integral es válida para los conjuntos que ocurren en aplicaciones típicas.
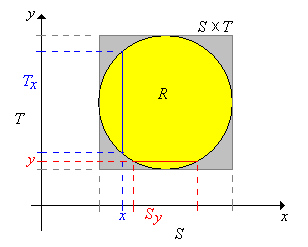
Supongamos ahora que\(X\) toma valores\(\R^j\),\(Y\) toma valores en\(\R^k\), y que\((X, Y)\) se distribuye uniformemente en un conjunto\(R \subseteq \R^{j+k}\). Entonces\( 0 \lt \lambda_{j+k}(R) \lt \infty \) y entonces la función conjunta de densidad de probabilidad\(f\) de\((X, Y)\) está dada por\( f(x, y) = 1 \big/ \lambda_{j+k}(R)\) for\( (x, y) \in R\). Ahora dejemos\(S\) y\(T\) sean las proyecciones de\(R\) onto\(\R^j\) y\(\R^k\) respectivamente, definidas de la siguiente manera:\[S = \left\{x \in \R^j: (x, y) \in R \text{ for some } y \in \R^k\right\}, \quad T = \left\{y \in \R^k: (x, y) \in R \text{ for some } x \in \R^j\right\} \] Obsérvese eso\(R \subseteq S \times T\). A continuación denotamos las secciones transversales en\(x \in S\) y en\(y \in T\), respectivamente, por\[T_x = \{t \in T: (x, t) \in R\}, \quad S_y = \{s \in S: (s, y) \in R\} \]
.png)
En la última sección sobre Distribuciones Conjuntas, vimos que aunque\((X, Y)\) se distribuya uniformemente, las distribuciones marginales de\(X\) y no\(Y\) son uniformes en general. Sin embargo, como muestra el siguiente teorema, las distribuciones condicionales son siempre uniformes.
Supongamos que\( (X, Y) \) se distribuye uniformemente en\( R \). Entonces
- La distribución condicional de\(Y\) dado\(X = x\) es uniforme\(T_x\) para cada uno\(x \in S\).
- La distribución condicional de\(X\) dado\(Y = y\) es uniforme\(S_y\) para cada uno\(y \in T\).
Prueba
Los resultados son simétricos, por lo que probaremos (a). Recordemos que\( X \) tiene PDF\(g\) dado por\[ g(x) = \int_{T_x} f(x, y) \, dy = \int_{T_x} \frac{1}{\lambda_{j+k}(R)} \, dy = \frac{\lambda_k(T_x)}{\lambda_{j+k}(R)}, \quad x \in S \] De ahí para\( x \in S \), el PDF condicional de\( Y \) dado\( X = x \) es\[ h(y \mid x) = \frac{f(x, y)}{g(x)} = \frac{1}{\lambda_k(T_x)}, \quad y \in T_x \] y este es el PDF de la distribución uniforme en\( T_x \).
Encuentra la densidad condicional de cada variable dado un valor de la otra, y determina si las variables son independientes, en cada uno de los siguientes casos:
- \((X, Y)\)se distribuye uniformemente en el cuadrado\(R = (-6, 6)^2\).
- \((X, Y)\)se distribuye uniformemente en el triángulo\(R = \{(x, y) \in \R^2: -6 \lt y \lt x \lt 6\}\).
- \((X, Y)\)se distribuye uniformemente en el círculo\(R = \{(x, y) \in \R^2: x^2 + y^2 \lt 36\}\).
Contestar
Se denota el PDF condicional de\(X\) dado\(Y = y\)\(x \mapsto g(x \mid y)\). Se denota el PDF condicional de\(Y\) dado\(X = x\)\(y \mapsto h(y \mid x)\).
-
- Para\(y \in (-6, 6)\),\(g(x \mid y) = \frac{1}{12}\) para\(x \in (-6, 6)\).
- Para\(x \in (-6, 6)\),\(h(y \mid x) = \frac{1}{12}\) para\(y \in (-6, 6)\).
- \(X\),\(Y\) son independientes.
-
- Para\(y \in (-6, 6)\),\(g(x \mid y) = \frac{1}{6 - y}\) para\(x \in (y, 6)\)
- Para\(x \in (-6, 6)\),\(h(y \mid x) = \frac{1}{x + 6}\) para\(y \in (-6, x)\)
- \(X\),\(Y\) son dependientes.
-
- Para\(y \in (-6, 6)\),\(g(x \mid y) = \frac{1}{2 \sqrt{36 - y^2}}\) para\(x \in \left(-\sqrt{36 - y^2}, \sqrt{36 - y^2}\right)\)
- Para\(x \in (-6, 6)\),\(g(x \mid y) = \frac{1}{2 \sqrt{36 - x^2}}\) para\(y \in \left(-\sqrt{36 - x^2}, \sqrt{36 - x^2}\right)\)
- \(X\),\(Y\) son dependientes.
En el experimento uniforme bivariado, ejecutar la simulación 1000 veces en cada uno de los siguientes casos. Observe los puntos en la gráfica de dispersión y las gráficas de las distribuciones marginales.
- cuadrado
- triángulo
- círculo
Supongamos que\((X, Y, Z)\) se distribuye uniformemente en\(R = \{(x, y, z) \in \R^3: 0 \lt x \lt y \lt z \lt 1\}\).
- Encuentra la densidad condicional de cada par de variables dado un valor de la tercera variable.
- Encuentra la densidad condicional de cada variable dados los valores de las otras dos.
Contestar
Los subíndices 1, 2 y 3 corresponden a las variables\( X \)\( Y \), y\( Z \), respectivamente. Obsérvese que las condiciones\((x, y, z)\) en cada caso son las de la definición del dominio\(R\). Se establecen de manera diferente para enfatizar el dominio del PDF condicional en contraposición a los valores dados, que funcionan como parámetros. Obsérvese también que cada distribución es uniforme en la región apropiada.
- Para\(0 \lt z \lt 1\),\(f_{1, 2 \mid 3}(x, y \mid z) = \frac{2}{z^2}\) para\(0 \lt x \lt y \lt z\)
- Para\(0 \lt y \lt 1\),\(f_{1, 3 \mid 2}(x, z \mid y) = \frac{1}{y (1 - y)}\) para\(0 \lt x \lt y\) y\(y \lt z \lt 1\)
- Para\(0 \lt x \lt 1\),\(f_{2, 3 \mid 1}(y, z \mid x) = \frac{2}{(1 - x)^2}\) para\(x \lt y \lt z \lt 1\)
- Para\(0 \lt y \lt z \lt 1\),\(f_{1 \mid 2, 3}(x \mid y, z) = \frac{1}{y}\) para\(0 \lt x \lt y\)
- Para\(0 \lt x \lt z \lt 1\),\(f_{2 \mid 1, 3}(y \mid x, z) = \frac{1}{z - x}\) para\(x \lt y \lt z\)
- Para\(0 \lt x \lt y \lt 1\),\(f_{3 \mid 1, 2}(z \mid x, y) = \frac{1}{1 - y}\) para\(y \lt z \lt 1\)
La distribución hipergeométrica multivariada
Recordemos la discusión de la distribución hipergeométrica (multivariante) dada en la última sección sobre distribuciones conjuntas. Al igual que en esa discusión, supongamos que una población consiste en\(m\) objetos, y que cada objeto es uno de cuatro tipos. Hay\(a\) objetos de tipo 1,\(b\) objetos de tipo 2, y\(c\) objetos de tipo 3, y\(m - a - b - c\) objetos de tipo 0. Muestreamos\(n\) objetos de la población al azar, y sin reemplazo. Los parámetros\(a\),\(b\),\(c\), y\(n\) son enteros no negativos con\(a + b + c \le m\) y\(n \le m\). Denote el número de objetos tipo 1, 2 y 3 en la muestra por\(X\)\(Y\), y\(Z\), respectivamente. De ahí que el número de objetos tipo 0 en la muestra sea\(n - X - Y - Z\). En los siguientes ejercicios,\(x, \, y, \, z \in \N\).
Supongamos que\(z \le c\) y\(n - m + c \le z \le n\). Entonces la distribución condicional de\((X, Y)\) dado\(Z = z\) es hipergeométrica, y tiene la función de densidad de probabilidad definida por\[ g(x, y \mid z) = \frac{\binom{a}{x} \binom{b}{y} \binom{m - a - b - c}{n - x - y - z}}{\binom{m - c}{n - z}}, \quad x + y \le n - z\]
Prueba
Este resultado se puede probar analíticamente pero un argumento combinatorio es mejor. La esencia del argumento es que estamos seleccionando una muestra aleatoria de tamaño\(n - z\) sin reemplazo de una población de tamaño\(m - c\), con\(a\) objetos de tipo 1,\(b\) objetos de tipo 2 y\(m - a - b\) objetos de tipo 0. Las condiciones sobre\(z\) aseguran que\(\P(Z = z) \gt 0\), o equivalentemente, que los nuevos parámetros tengan sentido.
Supongamos que\(y \le b\)\(z \le c\),, y\(n - m + b \le y + z \le n\). Entonces la distribución condicional de\(X\) dada\(Y = y\) y\(Z = z\) es hipergeométrica, y tiene la función de densidad de probabilidad definida por\[ g(x \mid y, z) = \frac{\binom{a}{x} \binom{m - a - b - c}{n - x - y - z}}{\binom{m - b - c}{n - y - z}}, \quad x \le n - y - z\]
Prueba
Nuevamente, este resultado se puede probar analíticamente, pero un argumento combinatorio es mejor. La esencia del argumento es que estamos seleccionando una muestra aleatoria de tamaño\(n - y - z\) de una población de tamaño\(m - b - c\), con\(a\) objetos de tipo 1 y\(m - a - b - c\) objetos tipo 0. Las condiciones sobre\(y\) y\(z\) aseguran eso\(\P(Y = y, Z = z) \gt 0\), o equivalentemente que los nuevos parámetros tengan sentido.
Estos resultados generalizan de manera completamente directa a una población con cualquier número de tipos. En resumen, si un vector aleatorio tiene una distribución hipergeométrica, entonces la distribución condicional de algunas de las variables, dados valores de las otras variables, también es hipergeométrica. Además, claramente no es necesario recordar las horrendas fórmulas en los dos teoremas anteriores. Solo necesita reconocer el problema como muestreo sin reemplazo de una población multitipo, para luego identificar el número de objetos de cada tipo y el tamaño de la muestra. La distribución hipergeométrica y la distribución hipergeométrica multivariada se estudian con más detalle en el capítulo Modelos de Muestreo Finito.
En una población de 150 votantes, 60 son demócratas y 50 republicanos y 40 son independientes. Se selecciona al azar una muestra de 15 electores, sin reemplazo. Vamos a\(X\) denotar el número de demócratas en la muestra y\(Y\) el número de republicanos en la muestra. Dar la función de densidad de probabilidad de cada uno de los siguientes:
- \((X, Y)\)
- \(X\)
- \(Y\)dado\(X = 5\)
Contestar
- \(f(x, y) = \frac{1}{\binom{150}{15}} \binom{60}{x} \binom{50}{y} \binom{40}{15 - x - y}\)para\(x + y \le 15\)
- \(g(x) = \frac{1}{\binom{150}{15}} \binom{60}{x} \binom{90}{15 - x}\)para\(x \le 15\)
- \(h(y \mid 5) = \frac{1}{\binom{90}{10}} \binom{50}{y} \binom{40}{10 - y}\)para\(y \le 10\)
Recordemos que una mano de puente consiste en 13 cartas seleccionadas al azar y sin reemplazo de una baraja estándar de 52 cartas. Dejar\(X\),\(Y\), y\(Z\) denotar el número de espadas, corazones y diamantes, respectivamente, en la mano. Encuentre la función de densidad de probabilidad de cada uno de los siguientes:
- \((X, Y, Z)\)
- \((X, Y)\)
- \(X\)
- \((X, Y)\)dado\(Z = 3\)
- \(X\)dado\(Y = 3\) y\(Z = 2\)
Contestar
- \(f(x, y, z) = \frac{1}{\binom{52}{13}} \binom{13}{x} \binom{13}{y} \binom{13}{z} \binom{13}{13 - x - y - z}\)para\(x + y + z \le 13\).
- \(g(x, y) = \frac{1}{\binom{52}{13}} \binom{13}{x} \binom{13}{y} \binom{26}{13 - x - y}\)para\(x + y \le 13\)
- \(h(x) = \frac{1}{\binom{52}{13}} \binom{13}{x} \binom{39}{13 - x}\)para\(x \le 13\)
- \(g(x, y \mid 3) = \frac{1}{\binom{39}{10}} \binom{13}{x} \binom{13}{y} \binom{13}{10 - x - y}\)para\(x + y \le 10\)
- \(h(x \mid 3, 2) = \frac{1}{\binom{26}{8}} \binom{13}{x} \binom{13}{8 - x}\)para\(x \le 8\)
Ensayos Multinomiales
Recordemos la discusión de los ensayos multinomiales en la última sección sobre distribuciones conjuntas. Como en esa discusión, supongamos que tenemos una secuencia de ensayos\(n\) independientes, cada uno con 4 posibles resultados. En cada ensayo, el resultado 1 ocurre con probabilidad\(p\), el resultado 2 con probabilidad\(q\), el resultado 3 con probabilidad\(r\) y el resultado 0 con probabilidad\(1 - p - q - r\). Los parámetros\(p, \, q, \, r \in (0, 1)\), con\(p + q + r \lt 1\), y\(n \in \N_+\). Denote el número de veces que el resultado 1, el resultado 2 y el resultado 3 ocurren en los\(n\) ensayos por\(X\)\(Y\), y\(Z\) respectivamente. Por supuesto, el número de veces que se produce el resultado 0 es\(n - X - Y - Z\). En los siguientes ejercicios,\(x, \, y, \, z \in \N\).
Para\(z \le n\), la distribución condicional de\((X, Y)\) dado también\(Z = z\) es multinomial, y tiene la función de densidad de probabilidad.
\[ g(x, y \mid z) = \binom{n - z}{x, \, y} \left(\frac{p}{1 - r}\right)^x \left(\frac{q}{1 - r}\right)^y \left(1 - \frac{p}{1 - r} - \frac{q}{1 - r}\right)^{n - x - y - z}, \quad x + y \le n - z\]Prueba
Este resultado se puede probar analíticamente, pero un argumento de probabilidad es mejor. Primero,\( I \) denotemos el resultado de un juicio genérico. Entonces\( \P(I = 1 \mid I \ne 3) = \P(I = 1) / \P(I \ne 3) = p \big/ (1 - r) \). De igual manera,\( \P(I = 2 \mid I \ne 3) = q \big/ (1 - r) \) y\( \P(I = 0 \mid I \ne 3) = (1 - p - q - r) \big/ (1 - r) \). Ahora bien, la esencia del argumento es que efectivamente, tenemos ensayos\(n - z\) independientes, y en cada ensayo, el resultado 1 ocurre con probabilidad\(p \big/ (1 - r)\) y el resultado 2 con probabilidad\(q \big/ (1 - r)\).
Para\(y + z \le n\), la distribución condicional de\(X\) dado\(Y = y\) y\(Z = z\) es binomial, con la función de densidad de probabilidad
\[ h(x \mid y, z) = \binom{n - y - z}{x} \left(\frac{p}{1 - q - r}\right)^x \left(1 - \frac{p}{1 - q - r}\right)^{n - x - y - z},\quad x \le n - y - z\]Prueba
Nuevamente, este resultado se puede probar analíticamente, pero un argumento de probabilidad es mejor. Como antes,\( I \) denotemos el resultado de un juicio genérico. Entonces\( \P(I = 1 \mid I \notin \{2, 3\}) = p \big/ (1 - q - r) \) y\( \P(I = 0 \mid I \notin \{2, 3\}) = (1 - p - q - r) \big/ (1 - q - r) \). Así, la esencia del argumento es que efectivamente, tenemos juicios\(n - y - z\) independientes, y en cada ensayo, el resultado 1 ocurre con probabilidad\(p \big/ (1 - q - r)\).
Estos resultados se generalizan de una manera completamente sencilla a ensayos multinomiales con cualquier número de resultados de ensayos. En resumen, si un vector aleatorio tiene una distribución multinomial, entonces la distribución condicional de algunas de las variables, dados valores de las otras variables, también es multinomial. Además, claramente no es necesario recordar las fórmulas específicas en los dos ejercicios anteriores. Solo necesitas reconocer un problema como uno que involucra ensayos independientes, y luego identificar la probabilidad de cada resultado y el número de ensayos. La distribución binomial y la distribución multinomial se estudian con más detalle en el capítulo de Ensayos de Bernoulli.
Supongamos que los melocotones de un huerto se clasifican como pequeños, medianos o grandes. Cada durazno, independientemente de los demás, es pequeño con probabilidad\(\frac{3}{10}\), medio con probabilidad\(\frac{1}{2}\) y grande con probabilidad\(\frac{1}{5}\). En una muestra de 20 melocotones del huerto, vamos a\(X\) denotar el número de melocotones pequeños y\(Y\) el número de melocotones medianos. Dar la función de densidad de probabilidad de cada uno de los siguientes:
- \((X, Y)\)
- \(X\)
- \(Y\)dado\(X = 5\)
Contestar
- \(f(x, y) = \binom{20}{x, \, y} \left(\frac{3}{10}\right)^x \left(\frac{1}{2}\right)^y \left(\frac{1}{5}\right)^{20 - x - y}\)para\(x + y \le 20\)
- \(g(x) = \binom{20}{x} \left(\frac{3}{10}\right)^x \left(\frac{7}{10}\right)^{20 - x}\)para\(x \le 20\)
- \(h(y \mid 5) = \binom{15}{y} \left(\frac{5}{7}\right)^y \left(\frac{2}{7}\right)^{15 - y}\)para\(y \le 15\)
Para un dado dado torcido, de 4 lados, la cara 1 tiene probabilidad\(\frac{2}{5}\), la cara 2 tiene probabilidad\(\frac{3}{10}\), la cara 3 tiene probabilidad\(\frac{1}{5}\) y la cara 4 tiene probabilidad\(\frac{1}{10}\). Supongamos que el dado se lanza 50 veces. Dejar\(X\),\(Y\), y\(Z\) denotar el número de veces que se producen las puntuaciones 1, 2 y 3, respectivamente. Encuentre la función de densidad de probabilidad de cada uno de los siguientes:
- \((X, Y, Z)\)
- \((X, Y)\)
- \(X\)
- \((X, Y)\)dado\(Z = 5\)
- \(X\)dado\(Y = 10\) y\(Z = 5\)
Contestar
- \(f(x, y, z) = \binom{50}{x, \, y, \, z} \left(\frac{2}{5}\right)^x \left(\frac{3}{10}\right)^y \left(\frac{1}{5}\right)^z \left(\frac{1}{10}\right)^{50 - x - y - z}\)para\(x + y + z \le 50\)
- \(g(x, y) = \binom{50}{x, \, y} \left(\frac{2}{5}\right)^x \left(\frac{3}{10}\right)^y \left(\frac{3}{10}\right)^{50 - x - y}\)para\(x + y \le 50\)
- \(h(x) = \binom{50}{x} \left(\frac{2}{5}\right)^x \left(\frac{3}{5}\right)^{50 - x}\)para\(x \le 50\)
- \(g(x, y \mid 5) = \binom{45}{x, \, y} \left(\frac{1}{2}\right)^x \left(\frac{3}{8}\right)^y \left(\frac{1}{8}\right)^{45 - x - y}\)para\(x + y \le 45\)
- \(h(x \mid 10, 5) = \binom{35}{x} \left(\frac{4}{5}\right)^x \left(\frac{1}{4}\right)^{10 - x}\)para\(x \le 35\)
Distribuciones normales bivariadas
Las distribuciones conjuntas en los dos ejercicios siguientes son ejemplos de distribuciones normales bivariadas. Las distribuciones condicionales también son normales, una propiedad importante de la distribución normal bivariada. En general, las distribuciones normales son ampliamente utilizadas para modelar mediciones físicas sujetas a pequeños errores aleatorios. La distribución normal bivariada se estudia con más detalle en el capítulo sobre Distribuciones Especiales.
Supongamos que\((X, Y)\) tiene la distribución normal bivariada con la función de densidad de probabilidad\(f\) definida por\[f(x, y) = \frac{1}{12 \pi} \exp\left[-\left(\frac{x^2}{8} + \frac{y^2}{18}\right)\right], \quad (x, y) \in \R^2\]
- Encuentra la función de densidad de probabilidad condicional de\(X\) dado\(Y = y\) para\(y \in \R\).
- Encuentra la función de densidad de probabilidad condicional de\(Y\) dado\(X = x\) para\(x \in \R\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- Para\(y \in \R\),\(g(x \mid y) = \frac{1}{2 \sqrt{2 \pi}} e^{-x^2 / 8}\) para\(x \in \R\). Este es el PDF de la distribución normal con media 0 y varianza 4.
- Para\(x \in \R\),\(h(y \mid x) = \frac{1}{3 \sqrt{2 \pi}} e^{-y^2 / 18}\) para\(y \in \R\). Este es el PDF de la distribución normal con media 0 y varianza 9.
- \(X\)y\(Y\) son independientes.
Supongamos que\((X, Y)\) tiene la distribución normal bivariada con la función de densidad de probabilidad\(f\) definida por\[f(x, y) = \frac{1}{\sqrt{3} \pi} \exp\left[-\frac{2}{3} (x^2 - x y + y^2)\right], \quad (x, y) \in \R^2\]
- Encuentra la función de densidad de probabilidad condicional de\(X\) dado\(Y = y\) para\(y \in \R\).
- Encuentra la función de densidad de probabilidad condicional de\(Y\) dado\(X = x\) para\(x \in \R\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- Para\(y \in \R\),\(g(x \mid y) = \sqrt{\frac{2}{3 \pi}} e^{-\frac{2}{3} (x - y / 2)^2}\) para\( x \in \R\). Este es el PDF de la distribución normal con media\(y/2\) y varianza\(3/4\).
- Para\(x \in \R\),\(h(y \mid x) = \sqrt{\frac{2}{3 \pi}} e^{-\frac{2}{3} (y - x / 2)^2}\) para\(y \in \R\). Este es el PDF de la distribución normal con media\(x/2\) y varianza\(3/4\).
- \(X\)y\(Y\) son dependientes.
Mezclas de Distribuciones
Con nuestros conjuntos habituales\(S\) y\(T\), como arriba, supongamos que\(P_x\) es una medida de probabilidad\(T\) para cada uno\(x \in S\). Supongamos también que\(g\) es una función de densidad de probabilidad en\(S\). Podemos obtener una nueva medida de probabilidad\(T\) al promediar (o mezclar) las distribuciones dadas según\(g\).
Primero supongamos que\(g\) es la función de densidad de probabilidad de una distribución discreta en el conjunto contable\(S\). Entonces la función\(\P\) definida a continuación es una medida de probabilidad en\(T\):\[ \P(B) = \sum_{x \in S} g(x) P_x(B), \quad B \subseteq T \]
Prueba
Claramente\( \P(B) \ge 0 \) para\( B \subseteq T \) y\( \P(T) = \sum_{x \in S} g(x) \, 1 = 1 \). Supongamos que\( \{B_i: i \in I\} \) es una colección contable y disjunta de subconjuntos de\( T \). Entonces se justifica\[ \P\left(\bigcup_{i \in I} B_i\right) = \sum_{x \in S} g(x) P_x\left(\bigcup_{i \in I} B_i\right) = \sum_{x \in S} g(x) \sum_{i \in I} P_x(B_i) = \sum_{i \in I} \sum_{x \in S} g(x) P_x(B_i) = \sum_{i \in I} \P(B_i) \] invertir el orden de suma ya que los términos no son negativos.
En la configuración del teorema anterior, supongamos que\(P_x\) tiene función de densidad de probabilidad\(h_x\) para cada uno\(x \in S\). Entonces\(\P\) tiene la función de densidad de probabilidad\(h\) dada por\[ h(y) = \sum_{x \in S} g(x) h_x(y), \quad y \in T \]
Prueba
Como es habitual, consideraremos los casos discretos y continuos para las distribuciones por\(T\) separado.
- Supongamos que\(T\) es contable para que\(P_x\) sea una medida de probabilidad discreta para cada uno\(x \in S\). Por definición, para cada uno\(x \in S\),\(h_x(y) = \P_x(\{y\})\) para\(y \in T\). Entonces la función de densidad de probabilidad\(h\) de\(P\) viene dada por\[h(y) = P(\{y\}) = \sum_{x \in S} g(x) P_x(\{y\}) = \sum_{x \in S} g(x) h_x(y), \quad y \in T\]
- Supongamos ahora que\(P_x\) tiene una distribución continua en\(T \subseteq R^k\), con PDF\(g_x\) para cada uno\(x \in S\), Para\(B \subseteq T\),\[ \P(B) = \sum_{x \in S} g(x) P_x(B) = \sum_{x \in S} g(x) \int_B h_x(y) \, dy = \int_B \sum_{x \in S} g(x) h_x(y) \, dy = \int_B h(y) \, dy \] Así que por definición,\(h\) es el PDF de\(\P\). Nuevamente, el intercambio de suma e integral se justifica porque las funciones no son negativas. Técnicamente, también necesitamos\(y \mapsto h_x(y)\) ser medibles para\(x \in S\) que la integral tenga sentido.
Por el contrario, dada una función de densidad de probabilidad\( g \) on\( S \) y una función\( h_x \) de densidad de probabilidad\( T \) para cada uno\( x \in S \), la función\( h \) definida en el teorema anterior es una función de densidad de probabilidad on\( T \).
Supongamos ahora que\(g\) es la función de densidad de probabilidad de una distribución continua en\(S \subseteq \R^j\). Entonces la función\(\P\) definida a continuación es una medida de probabilidad en\(T\):\[ \P(B) = \int_S g(x) P_x(B) dx, \quad B \subseteq T\]
Prueba
La prueba es igual que la prueba del Teorema (45) con integrales en lugar de\( S \) reemplazar las sumas sobre\( S \). Claramente\( \P(B) \ge 0 \) para\( B \subseteq T \) y\( \P(T) = \int_S g(x) \, P_x(T) \, dx = \int_S g(x) \, dx = 1 \). Supongamos que\( \{B_i: i \in I\} \) es una colección contable y disjunta de subconjuntos de\( T \). Entonces se justifica\[ \P\left(\bigcup_{i \in I} B_i\right) = \int_S g(x) P_x\left(\bigcup_{i \in I} B_i\right) = \int_S g(x) \sum_{i \in I} P_x(B_i) = \sum_{i \in I} \int_S g(x) P_x(B_i) = \sum_{i \in I} \P(B_i) \] invertir la integral y la suma ya que los términos son no negativos. Técnicamente, necesitamos que los subconjuntos\(T\) y el mapeo\(x \mapsto P_x(B)\) sean medibles.
En la configuración del teorema anterior, supongamos que\(P_x\) es una distribución discreta (respectivamente continua) con función de densidad de probabilidad\(h_x\) para cada uno\(x \in S\). Entonces también\(\P\) es discreto (respectivamente continuo) con la función de densidad de probabilidad\(h\) dada por\[ h(y) = \int_S g(x) h_x(y) dx, \quad y \in T\]
Prueba
La prueba es igual que la prueba del Teorema (46) con integrales en lugar de\( S \) reemplazar las sumas sobre\( S \).
- Supongamos que\(T\) es contable para que\(P_x\) sea una medida de probabilidad discreta para cada uno\(x \in S\). Por definición, para cada uno\(x \in S\),\(h_x(y) = \P_x(\{y\})\) para\(y \in T\). Entonces la función\(h\) de densidad de probabilidad de\(P\) es dada por\[h(y) = P(\{y\}) = \int_S g(x) P_x(\{y\}) \, dx = \int_S g(x) h_x(y) \, dx, \quad y \in T\] Técnicamente, necesitamos\(x \mapsto P_x(\{y\}) = h_x(y)\) ser medibles para\(y \in T\).
- Supongamos ahora que\(P_x\) tiene una distribución continua en\(T \subseteq R^k\), con PDF\(g_x\) para cada uno\(x \in S\), Para\(B \subseteq T\),\[ \P(B) = \int_S g(x) P_x(B) \, dx = \int_S g(x) \int_B h_x(y) \, dy \, dx = \int_B \int_S g(x) h_x(y) \, dx \, dy = \int_B h(y) \, dy \] Así que por definición,\(h\) es el PDF de\(\P\). Nuevamente, el intercambio de suma e integral se justifica porque las funciones no son negativas. Técnicamente, también necesitamos\((x, y) \mapsto h_x(y)\) ser medibles para que la integral tenga sentido.
En ambos casos,\(\P\) se dice que la distribución es una mezcla del conjunto de distribuciones\(\{P_x: x \in S\}\), con densidad de mezcla\(g\).
Se puede tener una mezcla de distribuciones, sin tener variables aleatorias definidas en un espacio de probabilidad común. Sin embargo, las mezclas están íntimamente relacionadas con distribuciones condicionales. Volviendo a nuestra configuración habitual, supongamos que\(X\) y\(Y\) son variables aleatorias para un experimento, tomando valores en\(S\) y\(T\) respectivamente y esa función de densidad de\(X\) probabilidad\(g\). El siguiente resultado es simplemente una reafirmación de la ley de probabilidad total.
La distribución de\(Y\) es una mezcla de las distribuciones condicionales de\(Y\) dada\(X = x\), sobre\(x \in S\), con densidad de mezcla\(g\).
Prueba
Sólo la notación es diferente.
- Si\(X\) tiene una distribución discreta en el conjunto contable\(S\), entonces\[\P(Y \in B) = \sum_{x \in S} g(x) \P(Y \in B \mid X = x), \quad B \subseteq T\]
- Si\(X\) tiene una distribución continua\(S \subseteq \R^j\) entonces\[\P(Y \in B) = \int_S g(x) \P(Y \in B \mid X = x) \, dx, \quad B \subseteq T\]
Por último observamos que una distribución mixta (con partes discretas y continuas) realmente es una mezcla, en el sentido de esta discusión.
Supongamos que\(\P\) es una distribución mixta en un conjunto\(T\). Entonces\(\P\) es una mezcla de una distribución discreta y una distribución continua.
Prueba
Recordemos que la distribución mixta significa que se\( T \) puede dividir en un conjunto contable\( D \) y un conjunto\( C \subseteq \R^n \) para algunos\( n \in \N_+ \) con las propiedades que\( \P(\{x\}) \gt 0 \) for\( x \in D \),\( \P(\{x\}) = 0 \) for\( x \in C \), y\( p = \P(D) \in (0, 1) \). Dejar\( S = \{d, c\} \) y definir el PDF\( g \) en\( S \) por\( g(d) = p \) y\( g(c) = 1 - p \). Recordemos que la distribución condicional\( P_d \) definida por\( P_d(A) = \P(A \cap D) / \P(D) \) for\( A \subseteq T \) es una distribución discreta en\( T \) y de manera similar la distribución condicional\( P_c \) definida por\( P_c(A) = \P(A \cap C) / \P(C) \) for\( A \subseteq T \) es una distribución continua en\( T \). Claramente con esta configuración,\[ \P(A) = g(c) P_c(A) + g(d) P_d(A), \quad A \subseteq T \]


