3.6: Funciones de distribución y cuantiles
- Page ID
- 151590
Como es habitual, nuestro punto de partida es un experimento aleatorio modelado por un espacio con probabilidad\((\Omega, \mathscr F, \P)\). Entonces, para revisar,\(\Omega\) es el conjunto de resultados,\(\mathscr F\) es la colección de eventos, y\(\P\) es la medida de probabilidad en el espacio muestral\((\Omega, \mathscr F)\). En esta sección, estudiaremos dos tipos de funciones que se pueden utilizar para especificar la distribución de una variable aleatoria de valor real.
Funciones de distribución
Definición
Supongamos que\(X\) es una variable aleatoria con valores en\(\R\). La función de distribución (acumulativa) de\(X\) es la función\(F: \R \to [0, 1]\) definida por\[ F(x) = \P(X \le x), \quad x \in \R\]
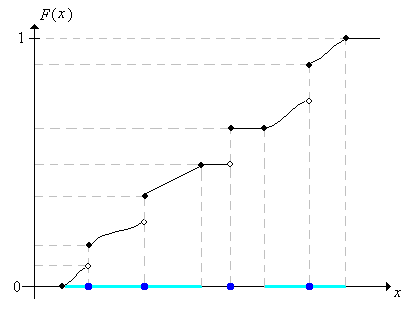
La función de distribución es importante porque tiene sentido para cualquier tipo de variable aleatoria, independientemente de si la distribución es discreta, continua o incluso mixta, y porque determina completamente la distribución de\(X\). En la siguiente imagen, el sombreado claro pretende representar una distribución continua de probabilidad, mientras que los puntos más oscuros representan puntos de probabilidad positiva;\(F(x)\) es la masa de probabilidad total a la izquierda de (e incluyendo)\(x\).

Propiedades Básicas
Algunas propiedades básicas caracterizan completamente las funciones de distribución. Notacionalmente, será útil abreviar los límites de\(F\) desde la izquierda y la derecha en\(x \in \R\), y en\(\infty\) y de la\(-\infty\) siguiente manera:\[F(x^+) = \lim_{t \downarrow x} F(t), \; F(x^-) = \lim_{t \uparrow x} F(t), \; F(\infty) = \lim_{t \to \infty} F(t), \; F(-\infty) = \lim_{t \to -\infty} F(t) \]
Supongamos que\( F \) es la función de distribución de una variable aleatoria de valor real\( X \).
- \(F\)está aumentando: si\(x \le y\) entonces\(F(x) \le F(y)\).
- \(F(x^+) = F(x)\)para\(x \in \R\). Así,\(F\) es continuo desde la derecha.
- \(F(x^-) = \P(X \lt x)\)para\(x \in \R\). Así,\(F\) tiene límites desde la izquierda.
- \(F(-\infty) = 0\).
- \(F(\infty) = 1\).
Prueba
El siguiente resultado muestra cómo se puede usar la función de distribución para calcular la probabilidad que\(X\) está en un intervalo. Recordemos que una distribución de probabilidad on\(\R\) está completamente determinada por las probabilidades de intervalos; así, la función de distribución determina la distribución de\(X\).
Supongamos nuevamente que\( F \) es la función de distribución de una variable aleatoria de valor real\( X \). Si\(a, \, b \in \R\) con\(a \lt b\) entonces
- \(\P(X = a) = F(a) - F(a^-)\)
- \(\P(a \lt X \le b) = F(b) - F(a)\)
- \(\P(a \lt X \lt b) = F(b^-) - F(a)\)
- \(\P(a \le X \le b) = F(b) - F(a^-)\)
- \(\P(a \le X \lt b) = F(b^-) - F(a^-)\)
Prueba
Estos resultados se derivan de la definición, las propiedades básicas, y la regla de diferencia:\(\P(B \setminus A) = \P(B) - \P(A) \) si\( A, \, B \) son eventos y\( A \subseteq B\).
- \(\{X = a\} = \{X \le a\} \setminus \{X \lt a\}\), entonces\(\P(X = a) = \P(X \le a) - \P(X \lt a) = F(a) - F(a^-)\).
- \(\{a \lt X \le b\} = \{X \le b\} \setminus \{X \le a\}\), entonces\(\P(a \lt X \le b) = \P(X \le b) - \P(X \le a) = F(b) - F(a)\).
- \(\{a \lt X \lt b\} = \{X \lt b\} \setminus \{X \le a\}\), entonces\(\P(a \lt X \lt b) = \P(X \lt b) - \P(X \le a) = F(b^-) - F(a)\).
- \(\{a \le X \le b\} = \{X \le b\} \setminus \{X \lt a\}\), entonces\(\P(a \le X \le b) = \P(X \le b) - \P(X \lt a) = F(b) - F(a^-)\).
- \(\{a \le X \lt b\} = \{X \lt b\} \setminus \{X \lt a\}\), entonces\(\P(a \le X \lt b) = \P(X \lt b) - \P(X \lt a) = F(b^-) - F(a^-)\).
Por el contrario, si una función\(F: \R \to [0, 1]\) satisface las propiedades básicas, entonces las fórmulas anteriores definen una distribución de probabilidad on\(\R\), con\(F\) como la función de distribución. Para más información sobre este punto, lee la sección sobre Existencia y Singularidad.
Si\(X\) tiene una distribución continua, entonces la función de distribución\(F\) es continua.
Prueba
Si\( X \) tiene una distribución continua, entonces por definición,\( \P(X = x) = 0 \) así que\( \P(X \lt x) = \P(X \le x) \) para\( x \in \R \). De ahí que a partir de la parte (a) del teorema anterior,\( F(x^-) = F(x^+) = F(x) \).
Así, los dos significados de continuo se unen: la distribución continua y la función continua en el sentido del cálculo. A continuación, recuerde que la distribución de una variable aleatoria de valor real\( X \) es simétrica alrededor de un punto\( a \in \R \) si la distribución de\( X - a \) es la misma que la distribución de\( a - X \).
Supongamos que\(X\) tiene una distribución continua sobre\(\R\) eso es simétrica alrededor de un punto\(a\). Entonces la función de distribución\(F\) satisface\(F(a - t) = 1 - F(a + t)\) para\(t \in \R\).
Prueba
Desde\( X - a \) y\( a - X \) tienen la misma distribución,\[ F(a - t) = \P(X \le a - t) = \P(X - a \le -t) = \P(a - X \le -t) = \P(X \ge a + t) = 1 - F(a + t) \]
Relación con las funciones de densidad
Existen relaciones simples entre la función de distribución y la función de densidad de probabilidad. Recordemos que si\(X\) toma valor en\(S \subseteq \R\) y tiene función de densidad de probabilidad\(f\), podemos extender\(f\) a todos\(\R\) por la convención que\(f(x) = 0\) para\(x \in S^c\). Al igual que en Definición (1), es costumbre definir la función de distribución\(F\) en todos\(\R\), incluso si la variable aleatoria toma valores en un subconjunto.
Supongamos que\(X\) tiene una distribución discreta en un subconjunto contable\(S \subseteq \R\). Dejar\(f\) denotar la función de densidad de probabilidad y\(F\) la función de distribución.
- \(F(x) = \sum_{t \in S, \, t \le x} f(t)\)para\(x \in \R\)
- \(f(x) = F(x) - F(x^-)\)para\(x \in S\)
Prueba
- Esto se desprende de la definición del PDF de\( X \),\( f(t) = \P(X = t) \) para\( t \in S \), y la aditividad de probabilidad.
- Esto es una reexpresión de la parte (a) del teorema anterior.
Así,\(F\) es una función de paso con saltos en los puntos\(S\) adentro; el tamaño del salto en\(x\) es\(f(x)\).
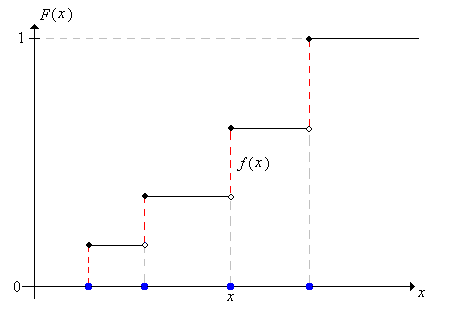
Hay un resultado análogo para una distribución continua con una función de densidad de probabilidad.
Supongamos que\(X\) tiene una distribución continua\(\R\) con función de densidad de probabilidad\(f\) y función de distribución\(F\).
- \(F(x) = \int_{-\infty}^x f(t) dt\)para\(x \in \R\).
- \(f(x) = F^\prime(x)\)si\(f\) es continuo en\(x\).
Prueba
El último resultado es la versión probabilística básica del teorema fundamental del cálculo. Para distribuciones mixtas, tenemos una combinación de los resultados en los dos últimos teoremas.
Supongamos que\(X\) tiene una distribución mixta, con una parte discreta en un subconjunto\(D \subseteq \R\) contable y una parte continua encendida\(\R \setminus D\). Let\(g\) denotar la función de densidad de probabilidad parcial de la parte discreta y asumir que la parte continua tiene función de densidad de probabilidad parcial\(h\). Dejar\(F\) denotar la función de distribución.
- \(F(x) = \sum_{t \in D, \, t \le x} g(t) + \int_{-\infty}^x h(t) dt\)para\(x \in \R\)
- \(g(x) = F(x) - F(x^-)\)para\(x \in D\)
- \(h(x) = F^\prime (x)\)si\(x \notin D\) y\(h\) es continuo en\(x\)
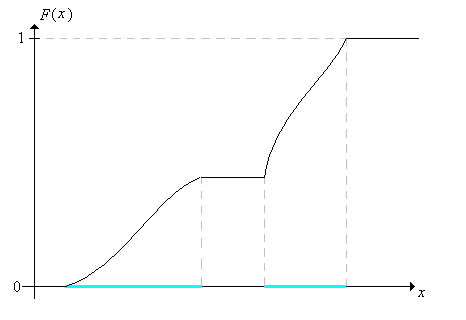
Volver a la gráfica de una función de distribución general. En un punto de probabilidad positiva, la probabilidad es el tamaño del salto. En un punto suave de la gráfica, la densidad de probabilidad continua es la pendiente.
Recordemos que la existencia de una función de densidad de probabilidad no está garantizada para una distribución continua, pero claro que la función de distribución siempre tiene perfecto sentido. La sección avanzada sobre continuidad absoluta y funciones de densidad tiene un ejemplo de una distribución continua en el intervalo\((0, 1)\) que no tiene función de densidad de probabilidad. La función de distribución es continua y aumenta estrictamente de 0 a 1 en el intervalo, ¡pero tiene 0 derivado en casi todos los puntos!
Naturalmente, la función de distribución puede definirse en relación con cualquiera de las distribuciones condicionales que hemos discutido. No hay conceptos nuevos involucrados, y todos los resultados anteriores se mantienen.
Confiabilidad
Supongamos nuevamente que\(X\) es una variable aleatoria de valor real con función de distribución\(F\). La función en la siguiente definición da claramente la misma información que\(F\).
La función\(F^c\) definida por\[ F^c(x) = 1 - F(x) = \P(X \gt x), \quad x \in \R\] es la función de distribución de cola derecha de\(X\). Dar las propiedades matemáticas de\(F^c\) análogas a las propiedades de\(F\) in (2).
Contestar
- \( F^c \)es decreciente.
- \( F^c(t) \to F^c(x) \)en\( t \downarrow x \) cuanto a\( x \in \R \), así\( F^c \) es continuo desde la derecha.
- \( F^c(t) \to \P(X \ge x) \)en\( t \uparrow x \) cuanto a\( x \in \R \), así\( F^c \) ha dejado límites.
- \( F^c(x) \to 0 \)como\( x \to \infty \).
- \( F^c(x) \to 1 \)como\( x \to -\infty \).
Entonces\(F\) podría llamarse la función de distribución de cola izquierda. Pero, ¿por qué tener dos funciones de distribución que dan esencialmente la misma información? La función de distribución de cola derecha, y las funciones relacionadas, surgen naturalmente en el contexto de la teoría de la confiabilidad. Para el resto de esta subsección, supongamos que\(T\) es una variable aleatoria con valores en\( [0, \infty) \) y que\( T \) tiene una distribución continua con función de densidad de probabilidad\( f \). Aquí están las definiciones importantes:
Supongamos que eso\( T \) representa la vida útil de un dispositivo.
- La función de distribución de cola derecha\( F^c \) es la función de confiabilidad de\( T \).
- La función\(h\) definida por\( h(t) = f(t) \big/ F^c(t)\) for\(t \ge 0 \) es la función de tasa de fallas de\( T \).
Para interpretar la función de confiabilidad, tenga en cuenta que\(F^c(t) = \P(T \gt t)\) es la probabilidad de que el dispositivo dure al menos unidades de\(t\) tiempo. Para interpretar la función de tasa de fallas, tenga en cuenta que si\( dt \) es pequeña
entonces\[ \P(t \lt T \lt t + dt \mid T \gt t) = \frac{\P(t \lt T \lt t + dt)}{\P(T \gt t)} \approx \frac{f(t) \, dt}{F^c(t)} = h(t) \, dt \] Así\(h(t) \, dt\) es la probabilidad aproximada de que el dispositivo falle en el intervalo\((t, t + dt)\), dada la supervivencia hasta el tiempo\(t\). Además, al igual que la función de distribución y la función de confiabilidad, la función de tasa de falla también determina completamente la distribución de\(T\).
La función de confiabilidad se puede expresar en términos de la función de tasa de falla mediante\[ F^c(t) = \exp\left(-\int_0^t h(s) \, ds\right), \quad t \ge 0 \]
Prueba
En los puntos de continuidad de\( f \) tenemos\( \frac{d}{dt}F^c(t) = - f(t) \). De ahí
\[ \int_0^t h(s) \, ds = \int_0^t \frac{f(s)}{F^c(s)} \, ds = \int_0^t -\frac{\frac{d}{ds}F^c(s)}{F^c(s)} \, ds = -\ln\left[F^c(t)\right] \]La función de tasa de fallas\(h\) satisface las siguientes propiedades:
- \(h(t) \ge 0\)para\(t \ge 0\)
- \(\int_0^\infty h(t) \, dt = \infty\)
Prueba
- Esto se desprende de la definición.
- Esto se desprende del resultado anterior y el hecho de que\( F^c(t) \to 0 \) como\( t \to \infty \).
Por el contrario, una función que satisface estas propiedades es la función de tasa de fallas para una distribución continua en\( [0, \infty) \):
Supongamos que\(h: [0, \infty) \to [0, \infty) \) es continuo por partes y\(\int_0^\infty h(t) \, dt = \infty\). Entonces la función\( G \) definida por\[ F^c(t) = \exp\left(-\int_0^t h(s) \, ds\right), \quad t \ge 0 \] es una función de confiabilidad para una distribución continua en\( [0, \infty) \)
Prueba
La función\( F^c \) es continua, decreciente, y satisface\( F^c(0) = 1 \) y\( F^c(t) \to 0 \) como\( t \to \infty \). De ahí\( F = 1 - F^c \) es la función de distribución para una distribución continua en\( [0, \infty) \).
Funciones de distribución multivariante
Supongamos ahora que\(X\) y\(Y\) son variables aleatorias de valor real para un experimento (es decir, definidas en el mismo espacio de probabilidad), por lo que\((X, Y)\) es un vector aleatorio tomando valores en un subconjunto de\(\R^2\).
La función de distribución de\((X, Y)\) es la función\(F\) definida por\[ F(x, y) = \P(X \le x, Y \le y), \quad (x, y) \in \R^2\]
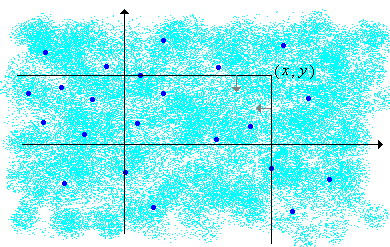
En la gráfica anterior, el sombreado claro pretende sugerir una distribución continua de la probabilidad, mientras que los puntos más oscuros representan puntos de probabilidad positiva. Así,\(F(x, y)\) es la masa de probabilidad total por debajo y a la izquierda (es decir, suroeste) del punto\((x, y)\). Al igual que en el caso de una sola variable, la función de distribución de determina\((X, Y)\) completamente la distribución de\((X, Y)\).
Supongamos que\(a, \, b, \, c, \, d \in \R\) con\(a \lt b\) y\(c \lt d\). Entonces\[ \P(a \lt X \le b, c \lt Y \le d) = F(b, d) - F(a, d) - F(b, c) + F(a, c) \]
Prueba
Tenga en cuenta que\( \{X \le a, Y \le d\} \cup \{X \le b, Y \le c\} \cup \{a \lt X \le b, c \lt Y \le d\} = \{X \le b, Y \le d\} \). La intersección de los dos primeros eventos es\( \{X \le a, Y \le c\} \) mientras que los eventos primero y tercero y el segundo y tercer eventos son disjuntos. Así, a partir de la regla de inclusión-exclusión tenemos\[ F(a, d) + F(b, c) + \P(a \lt X \le b, c \lt Y \le d) - F(a, c) = F(b, d) \]
Una distribución de probabilidad on\( \R^2 \) está completamente determinada por sus valores en rectángulos de la forma\( (a, b] \times (c, d] \), así como en el caso de una sola variable, se deduce que la función de distribución de determina\( (X, Y) \) completamente la distribución de\( (X, Y) \). Consulte la sección avanzada sobre existencia y singularidad de medidas positivas en el capítulo sobre Medidas de probabilidad para más detalles.
En el ajuste del resultado anterior, dé la fórmula apropiada a la derecha para todas las combinaciones posibles de desigualdades débiles y fuertes a la izquierda.
La función de distribución conjunta determina las funciones de distribución individuales (marginales).
Let\(F\) denotar la función de distribución de\((X, Y)\), y let\(G\) y\(H\) denotar las funciones de distribución de\(X\) y\(Y\), respectivamente. Entonces
- \(G(x) = F(x, \infty)\)para\( x \in \R \)
- \(H(y) = F(\infty, y)\)para\( y \in \R \)
Prueba
Estos resultados se derivan del teorema de continuidad para eventos crecientes. Por ejemplo, en el apartado a\[ \P(X \le x) = \P(X \le x, Y \lt \infty) = \lim_{y \to \infty} \P(X \le x, Y \le y) = \lim_{y \to \infty} F(x, y) \]
Por otro lado, no podemos recuperar la función de distribución\( (X, Y) \) de las funciones de distribución individuales, excepto cuando las variables son independientes.
Variables aleatorias\(X\) y\(Y\) son independientes si y solo si\[ F(x, y) = G(x) H(y), \quad (x, y) \in \R^2\]
Prueba
Si\( X \) y\( Y \) son independientes entonces\( F(x, y) = \P(X \le x, Y \le y) = \P(X \le x) \P(Y \le y) = G(x) H(y) \) para\( (x, y) \in \R^2 \). Por el contrario, supongamos\( F(x, y) = G(x) H(y) \) para\( (x, y) \in \R^2 \). Si\( a, \, b, \, c, \, d \in \R \) con\( a \lt b \) y\( c \lt d \) luego de (15),\ comienza {align}\ P (a\ lt X\ le b, c\ lt Y\ le d) & = G (b) H (d) - G (a) H (d) -G (b) H (c) + G (a) H (c)\\ & = [G (b) - G (a)] [H (d) - H (c))] =\ P (a\ lt X\ le b)\ P (c\ lt Y\ le d)\ end {align} así se deduce que\( X \) y\( Y \) son independientes. (Recordemos nuevamente que una distribución de probabilidad en\( \R^2 \) está completamente determinada por sus valores en rectángulos.)
Todos los resultados de esta subsección generalizan de manera directa a vectores aleatorios\(n\) -dimensionales. Sólo la notación es más complicada.
La función de distribución empírica
Supongamos ahora que\( X \) es una variable aleatoria de valor real para un experimento aleatorio básico y que repetimos los\( n \) tiempos del experimento de forma independiente. Esto genera (para el nuevo experimento compuesto) una secuencia de variables independientes\( (X_1, X_2, \ldots, X_n) \) cada una con la misma distribución que\( X \). En términos estadísticos, esta secuencia es una muestra aleatoria de tamaño\( n \) a partir de la distribución de\( X \). En la inferencia estadística, los valores observados\((x_1, x_2, \ldots, x_n)\) de la muestra aleatoria forman nuestros datos.
La función de distribución empírica, basada en los datos\( (x_1, x_2, \ldots, x_n) \), se define por\[ F_n(x) = \frac{1}{n} \#\left\{i \in \{1, 2, \ldots, n\}: x_i \le x\right\} = \frac{1}{n} \sum_{i=1}^n \bs{1}(x_i \le x), \quad x \in \R\]
Así,\(F_n(x)\) da la proporción de valores en el conjunto de datos que son menores o iguales a\(x\). La función\(F_n\) es un estimador estadístico de\(F\), basado en el conjunto de datos dado. Este concepto se explora con más detalle en la sección sobre la media muestral en el capítulo sobre Muestras Aleatorias. Además, la función de distribución empírica está relacionada con el proceso estocástico del puente browniano que se estudia en el capítulo sobre el movimiento browniano.
Funciones cuantiles
Definiciones
Supongamos nuevamente que\( X \) es una variable aleatoria de valor real con función de distribución\( F \).
Para\(p \in (0, 1)\), un valor de\(x\) tal que\( F(x^-) = \P(X \lt x) \le p\) y\(F(x) = \P(X \le x) \ge p\) se llama cuantil de orden\(p\) para la distribución.
En términos generales, un cuantil de orden\(p\) es un valor donde la gráfica de la función de distribución cruza (o salta)\(p\). Por ejemplo, en la imagen de abajo,\(a\) está el cuantil único de orden\(p\) y\(b\) es el cuantil único de orden\(q\). Por otro lado, los cuantiles de orden\(r\) forman el intervalo\([c, d]\), y además,\(d\) es un cuantil para todos los órdenes en el intervalo\([r, s]\). Obsérvese también que si\( X \) tiene una distribución continua (por lo que\( F \) es continua) y\( x \) es un cuantil de orden\( p \in (0, 1) \), entonces\( F(x) = p \).
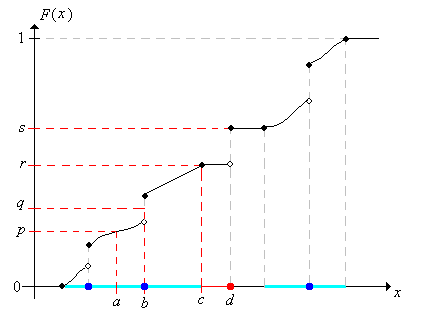
Obsérvese que existe una relación inversa de clases entre los cuantiles y los valores de distribución acumulativos, pero la relación es más complicada que la de una función y su función inversa ordinaria, porque la función de distribución no es uno a uno en general. Para muchos propósitos, es útil seleccionar un cuantil específico para cada orden; para ello se requiere definir una inversa generalizada de la función de distribución\( F \).
La función cuantil\( F^{-1} \) de\( X \) se define por\[ F^{-1}(p) = \min\{x \in \R: F(x) \ge p\}, \quad p \in (0, 1)\]
\( F^{-1} \)está bien definido
Dado que\(F\) es correcto continuo y creciente,\( \{x \in \R: F(x) \ge p\} \) es un intervalo de la forma\( [a, \infty) \). Así, el mínimo del conjunto es\( a \).
Tenga en cuenta que si aumenta\(F\) estrictamente de 0 a 1 en un intervalo\(S\) (de modo que la distribución subyacente es continua y se soporta en\(S\)), entonces\(F^{-1}\) es la inversa ordinaria de\(F\). No solemos definir la función quantile en los puntos finales 0 y 1. Si lo hiciéramos, tenga en cuenta que siempre\(F^{-1}(0)\) lo sería\(-\infty\).
Propiedades
El siguiente ejercicio justifica el nombre:\(F^{-1}(p)\) es el mínimo de los cuantiles de orden\(p\).
Vamos\(p \in (0, 1)\).
- \(F^{-1}(p)\)es un cuantil de orden\(p\).
- Si\(x\) es un cuantil de orden\(p\) entonces\(F^{-1}(p) \le x\).
Prueba
Vamos\( y = F^{-1}(p) \).
- Tenga en cuenta que\( F(y) \ge p \) por definición, y si\( x \lt y \) entonces\( F(x) \lt p \). De ahí\( F(y^-) \le p \). Por lo tanto\( y \) es un cuantil de orden\( p \).
- Supongamos que\( x \) es un cuantil de orden\( p \). Entonces\( F(x) \ge p \) así por definición,\( y \le x \).
Otras propiedades básicas de la función cuantil se dan en el siguiente teorema.
\(F^{-1}\)satisface las siguientes propiedades:
- \(F^{-1}\)está aumentando en\((0, 1)\).
- \(F^{-1}\left[F(x)\right] \le x\)para cualquiera\(x \in \R\) con\(F(x) \lt 1\).
- \(F\left[F^{-1}(p)\right] \ge p\)para cualquier\(p \in (0, 1)\).
- \(F^{-1}\left(p^-\right) = F^{-1}(p)\)para\(p \in (0, 1)\). Así\(F^{-1}\) es continuo desde la izquierda.
- \(F^{-1}\left(p^+\right) = \inf\{x \in \R: F(x) \gt p\}\)para\(p \in (0, 1)\). Así\(F^{-1}\) tiene límites desde la derecha.
Prueba
- Tenga en cuenta que si\( p, \; q \in (0, 1) \) con\( p \le q \), entonces\( \{x \in \R: F(x) \ge q\} \subseteq \{x \in \R: F(x) \ge p\} \).
- Esto se desprende de la definición:\( F^{-1}\left[F(x)\right] \) es el más pequeño\( y \in \R \) con\( F(y) \ge F(x) \).
- Esto también se desprende de la definición:\( F^{-1}(p) \) es un valor\( y \in \R \) satisfactorio\( F(y) \ge p \).
- Esto se desprende del hecho de que\( F \) es continuo desde la derecha
- Esto se desprende del hecho de que\( F \) tiene límites desde la izquierda.
Como siempre, la inversa de una función se obtiene esencialmente invirtiendo los roles de variables independientes y dependientes. En las gráficas siguientes, tenga en cuenta que los saltos de\(F\) se convierten en porciones planas de\(F^{-1}\) mientras que las porciones planas de\(F\) se convierten en saltos de\(F^{-1}\). Para\( p \in (0, 1) \), el conjunto de cuantiles de orden\( p \) es el intervalo cerrado y delimitado\( \left[F^{-1}(p), F^{-1}(p^+)\right] \). Así,\( F^{-1}(p) \) es el cuantil de orden más pequeño\( p \), como señalamos anteriormente, mientras que\( F^{-1}(p^+) \) es el mayor cuantil de orden\( p \).
.png)
Figura\(\PageIndex{7}\): Gráfica de la función de distribución
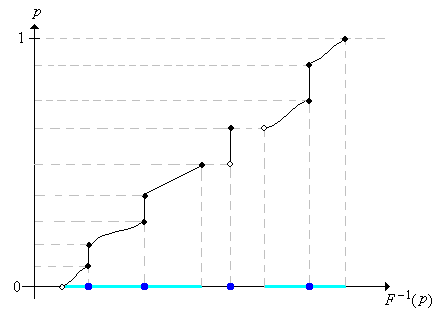
Figura\(\PageIndex{8}\): Gráfica de la función cuantil
La siguiente propiedad básica será útil para simular variables aleatorias, tema explorado en la sección sobre transformaciones de variables aleatorias.
Para\(x \in \R\) y\(p \in (0, 1)\),\(F^{-1}(p) \le x\) si y solo si\(p \le F(x)\).
Prueba
Supongamos que\( F^{-1}(p) \le x \). Entonces, ya que\( F \) va en aumento,\( F\left[F^{-1}(p)\right] \le F(x) \). Pero\( p \le F\left[F^{-1}(p)\right] \) por la parte (c) del resultado anterior, así\( p \le F(x) \). Por el contrario, supongamos que\( p \le F(x) \). Entonces, ya que\( F^{-1} \) va en aumento,\( F^{-1}(p) \le F^{-1}[F(x)] \). Pero\( F^{-1}[F(x)] \le x \) por la parte (b) del resultado anterior, así\( F^{-1}(p) \le x \).
Cuantiles especiales
Ciertos cuantiles son lo suficientemente importantes como para merecer nombres especiales.
Supongamos que\( X \) es una variable aleatoria de valor real.
- Un cuantil de orden\(\frac{1}{4}\) es un primer cuartil de la distribución.
- Un cuantil de orden\(\frac{1}{2}\) es una mediana o segundo cuartil de la distribución.
- Un cuantil de orden\(\frac{3}{4}\) es un tercer cuartil de la distribución.
Cuando sólo hay una mediana, se utiliza frecuentemente como medida del centro de la distribución, ya que divide el conjunto de valores de a\( X \) la mitad, por probabilidad. De manera más general, los cuartiles se pueden utilizar para dividir el conjunto de valores en cuartos, por probabilidad.
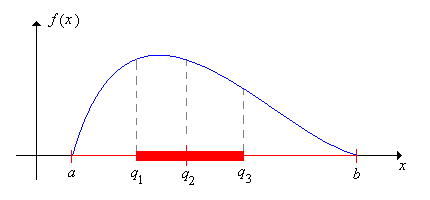
Asumiendo singularidad\(q_1\), let\(q_2\),, y\(q_3\) denotar el primero, segundo, y tercer cuartiles de\(X\), respectivamente, y let\(a = F^{-1}\left(0^+\right)\) y\(b = F^{-1}(1)\).
- El rango intercuartílico se define como\( q_3 - q_1 \).
- Los cinco parámetros\( (a, q_1, q_2, q_3, b) \) son referidos como el resumen de cinco números de la distribución.
Tenga en cuenta que el intervalo da\( [q_1, q_3] \) aproximadamente la mitad media de la distribución, por lo que el rango intercuartil, la longitud del intervalo, es una medida natural de la dispersión de la distribución alrededor de la mediana. Tenga en cuenta también que\(a\) y\(b\) son esencialmente los valores mínimo y máximo de\(X\), respectivamente, aunque por supuesto, es posible eso\( a = -\infty \) o\( b = \infty \) (o ambos). Colectivamente, los cinco parámetros dan una gran cantidad de información sobre la distribución en términos de centro, propagación y asimetría. Gráficamente, los cinco números a menudo se muestran como una gráfica de caja o una gráfica de caja y bigotes, que consiste en una línea que se extiende desde el valor mínimo\(a\) hasta el valor máximo\(b\), con una caja rectangular de\(q_1\) a\(q_3\), y bigotes
en \(a\), la mediana\(q_2\), y\(b\). En términos generales, los cinco números separan el conjunto de valores de\(X\) en 4 intervalos de probabilidad aproximada\(\frac{1}{4}\) cada uno.
Supongamos que\( X \) tiene una distribución continua que es simétrica alrededor de un punto\(a \in \R\). Si\(a + t\) es un cuantil de orden\(p \in (0, 1) \) entonces\(a - t\) es un cuantil de orden\(1 - p\).
Prueba
Tenga en cuenta que esta es la versión de función cuantil del resultado de simetría para la función de distribución. Si\( a + t \) es un qantile de orden\( p \) entonces (ya que\( X \) tiene una distribución continua)\( F(a + t) = p \). Pero entonces\( F(a - t) = 1 - F(a + t) = 1 - p \) así\( a - t \) es un cuantil de orden\( 1 - p \).
Ejemplos y Aplicaciones
Distribuciones de diferentes tipos
Dejar\(F\) ser la función definida por\[ F(x) = \begin{cases} 0, & x \lt 1\\ \frac{1}{10}, & 1 \le x \lt \frac{3}{2}\\ \frac{3}{10}, & \frac{3}{2} \le x \lt 2\\ \frac{6}{10}, & 2 \le x \lt \frac{5}{2}\\ \frac{9}{10}, & \frac{5}{2} \le x \lt 3\\ 1, & x \ge 3; \end{cases}\]
- Esboce la gráfica\(F\) y muestre que\(F\) es la función de distribución para una distribución discreta.
- Encuentre la función de densidad de probabilidad correspondiente\(f\) y dibuje la gráfica.
- Encuentra\(\P(2 \le X \lt 3)\) donde\(X\) tiene esta distribución.
- Encuentra la función cuantil y dibuja el gráfico.
- Encuentra el resumen de cinco números y dibuja el diagrama de caja.
Contestar
- Tenga en cuenta que\( F \) aumenta de 0 a 1, es una función de paso, y es correcto continuo.
- \(f(x) = \begin{cases} \frac{1}{10}, & x = 1 \\ \frac{1}{5}, & x = \frac{3}{2} \\ \frac{3}{10}, & x = 2 \\ \frac{3}{10}, & x = \frac{5}{2} \\ \frac{1}{10}, & x = 3 \end{cases}\)
- \(\P(2 \le X \lt 3) = \frac{3}{5}\)
- \(F^{-1}(p) = \begin{cases} 1, & 0 \lt p \le \frac{1}{10} \\ \frac{3}{2}, & \frac{1}{10} \lt p \le \frac{3}{10} \\ 2, & \frac{3}{10} \lt p \le \frac{6}{10} \\ \frac{5}{2}, & \frac{6}{10} \lt p \le \frac{9}{10} \\ 3, & \frac{9}{10} \lt p \le 1 \end{cases}\)
- \(\left(1, \frac{3}{2}, 2, \frac{5}{2}, 3\right)\)
Dejar\(F\) ser la función definida por
\[F(x) = \begin{cases} 0, & x \lt 0\\ \frac{x}{x + 1}, & x \ge 0 \end{cases}\]- Esbozar la gráfica\(F\) y mostrar que\(F\) es la función de distribución para una distribución continua.
- Encuentre la función de densidad de probabilidad correspondiente\(f\) y dibuje la gráfica.
- Encuentra\(\P(2 \le X \lt 3)\) donde\(X\) tiene esta distribución.
- Encuentra la función cuantil y dibuja el gráfico.
- Encuentra el resumen de cinco números y dibuja el diagrama de caja.
Contestar
- Tenga en cuenta que\( F \) es continuo y aumenta de 0 a 1.
- \(f(x) = \frac{1}{(x + 1)^2}, \quad x \gt 0\)
- \(\P(2 \le X \lt 3) = \frac{1}{12}\)
- \(F^{-1}(p) = \frac{p}{1 - p}, \quad 0 \lt p \lt 1\)
- \(\left(0, \frac{1}{3}, 1, 3, \infty\right)\)
La expresión\( \frac{p}{1 - p} \) que ocurre en la función cuantil en el último ejercicio se conoce como el odds ratio asociado\( p \), particularmente en el contexto del juego.
Dejar\(F\) ser la función definida por
\[ F(x) = \begin{cases} 0, & x \lt 0\\ \frac{1}{4} x, & 0 \le x \lt 1\\ \frac{1}{3} + \frac{1}{4} (x - 1)^2, & 1 \le x \lt 2\\ \frac{2}{3} + \frac{1}{4} (x - 2)^3, & 2 \le x \lt 3\\ 1, & x \ge 3 \end{cases}\]- Esbozar la gráfica\(F\) y mostrar que\(F\) es la función de distribución de una distribución mixta.
- Encuentre la función de densidad de probabilidad parcial de la parte discreta y esboce la gráfica.
- Encuentra la función de densidad de probabilidad parcial de la parte continua y dibuja la gráfica.
- Encuentra\(\P(2 \le X \lt 3)\) donde\(X\) tiene esta distribución.
- Encuentra la función cuantil y dibuja el gráfico.
- Encuentra el resumen de cinco números y dibuja el diagrama de caja.
Contestar
- Tenga en cuenta que\( F \) es continuo por piezas, aumenta de 0 a 1, y es continuo correcto.
- \(g(1) = g(2) = g(3) = \frac{1}{12}\)
- \(h(x) = \begin{cases} \frac{1}{4}, & 0 \lt x \lt 1 \\ \frac{1}{2}(x - 1), & 1 \lt x \lt 2 \\ \frac{3}{4}(x - 2)^2, & 2 \lt x \lt 3 \end{cases}\)
- \(\P(2 \le X \lt 3) = \frac{1}{3}\)
- \(F^{-1}(p) = \begin{cases} 4 p, & 0 \lt p \le \frac{1}{4} \\ 1, & \frac{1}{4} \lt p \le \frac{1}{3} \\ 1 + \sqrt{4(p - \frac{1}{3})}, & \frac{1}{3} \lt p \le \frac{7}{12} \\ 2, & \frac{7}{12} \lt p \le \frac{2}{3} \\ 2 + \sqrt[3]{4 (p - \frac{2}{3})}, & \frac{2}{3} \lt p \le \frac{11}{12} \\ 3, & \frac{11}{12} \lt p \le 1 \end{cases}\)
- \(\left(0, 1, 1 + \sqrt{\frac{2}{3}}, 2 + \sqrt[3]{\frac{1}{3}}, 3\right)\)
La distribución uniforme
Supongamos que\(X\) tiene función de densidad de probabilidad\(f(x) = \frac{1}{b - a}\) para\(x \in [a, b]\), donde\(a, \, b \in \R\) y\(a \lt b\).
- Encuentra la función de distribución y dibuja el gráfico.
- Encuentra la función cuantil y dibuja el gráfico.
- Calcular el resumen de cinco números.
- Esboce la gráfica de la función de densidad de probabilidad con la gráfica de caja en el eje horizontal.
Contestar
- \(F(x) = \frac{x - a}{b - a}, \quad a \le x \lt b\)
- \(F^{-1}(p) = a + (b - a) p, \quad 0 \le p \le 1\)
- \(\left(a, \frac{3 a + b}{4}, \frac{a + b}{2}, \frac{a + 3 b}{4}, b\right)\)
La distribución en el último ejercicio es la distribución uniforme en el intervalo\( [a, b] \). El punto final izquierdo\( a \) es el parámetro de ubicación y la longitud del intervalo\( w = b - a \) es el parámetro de escala. Los modelos de distribución uniforme que un punto eligió al azar
del intervalo, y se estudia con más detalle en el capítulo sobre Distribuciones Especiales.
En la calculadora de distribución especial, seleccione la distribución uniforme continua. Varíe los parámetros de ubicación y escala y anote la forma de la función de densidad de probabilidad y la función de distribución.
La distribución exponencial
Supongamos que\(T\) tiene función de densidad de probabilidad\(f(t) = r e^{-r t}\) para\(0 \le t \lt \infty\), donde\(r \gt 0\) es un parámetro.
- Encuentra la función de distribución y dibuja el gráfico.
- Encuentre la función de confiabilidad y dibuje el gráfico.
- Encuentre la función de tasa de fallas y dibuje el gráfico.
- Encuentra la función cuantil y dibuja el gráfico.
- Calcular el resumen de cinco números.
- Esboce la gráfica de la función de densidad de probabilidad con la gráfica de caja en el eje horizontal.
Contestar
- \(F(t) = 1 - e^{-r t}, \quad 0 \le t \lt \infty\)
- \(F^c(t) = e^{-r t}, \quad 0 \le t \lt \infty\)
- \(h(t) = r, \quad 0 \le t \lt \infty\)
- \(F^{-1}(p) = -\frac{1}{r} \ln(1 - p), \quad 0 \le p \lt 1\)
- \(\left(0, \frac{1}{r}[\ln 4 - \ln 3], \frac{1}{r} \ln 2, \frac{1}{r} \ln 4 , \infty\right)\)
La distribución en el último ejercicio es la distribución exponencial con parámetro de tasa\(r\). Obsérvese que esta distribución se caracteriza por el hecho de que tiene tasa de fallas constante (y esta es la razón para referirse\( r \) como el parámetro de tasa). El recíproco del parámetro rate es el parámetro scale. La distribución exponencial se utiliza para modelar tiempos de falla y otros tiempos aleatorios bajo ciertas condiciones, y se estudia en detalle en el capítulo sobre El proceso de Poisson.
En la calculadora de distribución especial, seleccione la distribución exponencial. Varíe el parámetro de escala\(b\) y anote la forma de la función de densidad de probabilidad y la función de distribución.
La distribución de Pareto
Supongamos que\(X\) tiene función de densidad de probabilidad\(f(x) = \frac{a}{x^{a+1}}\) para\(1 \le x \lt \infty\) donde\(a \gt 0\) es un parámetro.
- Encuentra la función de distribución.
- Encuentre la función de confiabilidad.
- Encuentra la función de tasa de fallas.
- Encuentra la función quantile.
- Calcular el resumen de cinco números.
- En el caso\(a = 2\), esboce la gráfica de la función de densidad de probabilidad con la gráfica de caja en el eje horizontal.
Contestar
- \(F(x) = 1 - \frac{1}{x^a}, \quad 1 \le x \lt \infty\)
- \(F^c(x) = \frac{1}{x^a}, \quad 1 \le x \lt \infty\)
- \(h(x) = \frac{a}{x}, \quad 1 \le x \lt \infty\)
- \(F^{-1}(p) = (1 - p)^{-1/a}, \quad 0 \le p \lt 1\)
- \(\left(1, \left(\frac{3}{4}\right)^{-1 / a}, \left(\frac{1}{2}\right)^{-1/a}, \left(\frac{1}{4}\right)^{-1/a}, \infty \right)\)
La distribución en el último ejercicio es la distribución de Pareto con parámetro shape\(a\), que lleva el nombre de Vilfredo Pareto. La distribución de Pareto es una distribución de cola pesada que a veces se utiliza para modelar el ingreso y algunas otras variables económicas. Se estudia en detalle en el capítulo sobre Distribuciones Especiales.
En la calculadora de distribución especial, seleccione la distribución de Pareto. Mantenga el valor predeterminado para el parámetro scale, pero varíe el parámetro shape y note la forma de la función de densidad y la función de distribución.
La distribución de Cauchy
Supongamos que\(X\) tiene función de densidad de probabilidad\( f(x) = \frac{1}{\pi (1 + x^2)} \) para\(x \in \R\).
- Encuentra la función de distribución y dibuja el gráfico.
- Encuentra la función cuantil y dibuja el gráfico.
- Compute el resumen de cinco números y el rango intercuartílico.
- Esboce la gráfica de la función de densidad de probabilidad con la gráfica de caja en el eje horizontal.
Contestar
- \(F(x) = \frac{1}{2} + \frac{1}{\pi} \arctan x, \quad x \in \R\)
- \(F^{-1}(p) = \tan\left[\pi\left(p - \frac{1}{2}\right)\right], \quad 0 \lt p \lt 1\)
- \((-\infty, -1, 0, 1, \infty)\),\(\text{IQR} = 2\)
La distribución en el último ejercicio es la distribución de Cauchy, que lleva el nombre de Augustin Cauchy. La distribución de Cauchy se estudia con más generalidad en el capítulo sobre Distribuciones Especiales.
En la calculadora de distribución especial, seleccione la distribución de Cauchy y mantenga los valores de los parámetros predeterminados. Anote la forma de la función de densidad y la función de distribución.
La distribución de Weibull
Let\(h(t) = k t^{k - 1}\) para\(0 \lt t \lt \infty\) donde\(k \gt 0\) es un parámetro.
- Esbozar la gráfica de\(h\) en los casos\(0 \lt k \lt 1\)\(k = 1\),\(1 \lt k \lt 2\),,\( k = 2 \), y\( k \gt 2 \).
- Mostrar que\(h\) es una función de tasa de fallas.
- Encuentre la función de confiabilidad y dibuje el gráfico.
- Encuentra la función de distribución y dibuja el gráfico.
- Encuentra la función de densidad de probabilidad y dibuja el gráfico.
- Encuentra la función cuantil y dibuja el gráfico.
- Calcular el resumen de cinco números.
Contestar
- \( h \)es decreciente y cóncavo hacia arriba si\( 0 \lt k \lt 1 \);\( h = 1 \) (constante) si\( k = 1 \);\( h \) está aumentando y cóncavo hacia abajo si\( 1 \lt k \lt 2 \);\( h(t) = t \) (lineal) si\( k = 2 \);\( h \) está aumentando y cóncavo hacia arriba si\( k \gt 2 \);
- \( h(t) \gt 0 \)para\( 0 \lt t \lt \infty \) y\( \int_0^\infty h(t) \, dt = \infty \)
- \(F^c(t) = \exp\left(-t^k\right), \quad 0 \le t \lt \infty\)
- \(F(t) = 1 - \exp\left(-t^k\right), \quad 0 \le t \lt \infty\)
- \(f(t) = k t^{k-1} \exp\left(-t^k\right), \quad 0 \le t \lt \infty\)
- \(F^{-1}(p) = [-\ln(1 - p)]^{1/k}, \quad 0 \le p \lt 1\)
- \(\left(0, [\ln 4 - \ln 3]^{1/k}, [\ln 2]^{1/k}, [\ln 4]^{1/k}, \infty\right)\)
La distribución en el ejercicio anterior son las distribuciones de Weibull con parámetro shape\(k\), que llevan el nombre de Walodi Weibull. La distribución de Weibull se estudia en detalle en el capítulo sobre Distribuciones Especiales. Dado que esta familia incluye tasas de falla crecientes, decrecientes y constantes, es ampliamente utilizada para modelar las vidas de varios tipos de dispositivos.
En la calculadora de distribución especial, seleccione la distribución de Weibull. Mantenga el parámetro de escala predeterminado, pero varíe el parámetro shape y observe la forma de la función de densidad y la función de distribución.
Distribuciones Beta
Supongamos que\(X\) tiene función de densidad de probabilidad\(f(x) = 12 x^2 (1 - x)\) para\(0 \le x \le 1\).
- Encuentra la función de distribución\(X\) y dibuja el gráfico.
- Encuentra\( \P\left(\frac{1}{4} \le X \le \frac{1}{2}\right) \).
- Compute el resumen de cinco números y el rango intercuartílico. Tendrás que aproximar los cuantiles.
- Esboce la gráfica de la función de densidad con la gráfica de caja en el eje horizontal.
Contestar
- \(F(x) = 4 x^3 - 3 x^4, \quad 0 \le x \le 1\)
- \(\P\left(\frac{1}{4} \le X \le \frac{1}{2}\right) = \frac{67}{256}\)
- \((0, 0.4563, 0.6413, 0.7570, 1)\),\(\text{IQR} = 0.3007\)
Supongamos que\(X\) tiene función de densidad de probabilidad\(f(x) = \frac{1}{\pi \sqrt{x (1 - x)}}\) para\(0 \lt x \lt 1\).
- Encuentra la función de distribución\(X\) y dibuja el gráfico.
- \( \P\left(\frac{1}{3} \le X \le \frac{2}{3}\right) \)Cómpiate.
- Encuentra la función cuantil y dibuja el gráfico.
- Compute el resumen de cinco números y el rango intercuartílico.
- Esboce la gráfica de la función de densidad de probabilidad con la gráfica de caja en el eje horizontal.
Contestar
- \(F(x) = \frac{2}{\pi} \arcsin\left(\sqrt{x}\right), \quad 0 \le x \le 1\)
- \(\P\left(\frac{1}{3} \le X \le \frac{2}{3}\right) = 0.2163\)
- \(F^{-1}(p) = \sin^2\left(\frac{\pi}{2} p\right), \quad 0 \lt p \lt 1\)
- \(\left(0, \frac{1}{2} - \frac{\sqrt{2}}{4}, \frac{1}{2}, \frac{1}{2} + \frac{\sqrt{2}}{4}, 1\right)\),\(\text{IQR} = \frac{\sqrt{2}}{2}\)
Las distribuciones en los dos últimos ejercicios son ejemplos de distribuciones beta. La distribución beta particular en el último ejercicio también se conoce como distribución arcoseno; la función de distribución explica el nombre. Las distribuciones beta se utilizan para modelar proporciones y probabilidades aleatorias, y ciertos otros tipos de variables aleatorias, y se estudian en detalle en el capítulo sobre Distribuciones especiales.
En la calculadora de distribución especial, seleccione la distribución beta. Para cada uno de los siguientes valores de parámetros, anote la ubicación y forma de la función de densidad y la función de distribución.
- \(a = 3\),\(b = 2\). Esto da la primera distribución beta anterior.
- \(a = b = \frac{1}{2}\). Esto da la distribución del arcoseno anterior
Distribución Logística
Dejemos\(F(x) = \frac{e^x}{1 + e^x}\) para\(x \in \R\).
- Mostrar que\(F\) es una función de distribución para una distribución continua, y bosquejar la gráfica.
- Calcular\( \P(-1 \le X \le 1) \) donde\(X\) es una variable aleatoria con función de distribución\(F\).
- Encuentra la función cuantil y dibuja el gráfico.
- Compute el resumen de cinco números y el rango intercuartílico.
- Encuentre la función de densidad de probabilidad y dibuje la gráfica con la gráfica de caja en el eje horizontal.
Contestar
- Tenga en cuenta que\( F \) es continuo, y aumenta de 0 a 1.
- \(\P(-1 \le X \le 1) = 0.4621\)
- \(F^{-1}(p) = \ln \left(\frac{p}{1 - p}\right), \quad 0 \lt p \lt 1\)
- \((-\infty, -\ln 3, 0, \ln 3, \infty)\)
- \(f(x) = \frac{e^x}{(1 + e^x)^2}, \quad x \in \R\)
La distribución en el último ejercicio es una distribución logística y la función cuantil se conoce como la función logit. La distribución logística se estudia en detalle en el capítulo sobre Distribuciones Especiales.
En la calculadora de distribución especial, seleccione la distribución logística y mantenga los valores de los parámetros predeterminados. Observe la forma de la función de densidad de probabilidad y la función de distribución.
Distribución de Valor Extremo
Dejemos\(F(x) = e^{-e^{-x}}\) para\(x \in \R\).
- Mostrar que\(F\) es una función de distribución para una distribución continua, y bosquejar la gráfica.
- Calcular\(\P(-1 \le X \le 1)\) donde\(X\) es una variable aleatoria con función de distribución\(F\).
- Encuentra la función cuantil y dibuja el gráfico.
- Calcular el resumen de cinco números.
- Encuentre la función de densidad de probabilidad y dibuje la gráfica con la gráfica de caja en el eje horizontal.
Contestar
- Tenga en cuenta que\( F \) es continuo, y aumenta de 0 a 1.
- \(\P(-1 \le X \le 1) = 0.6262\)
- \(F^{-1}(p) = -\ln(-\ln p), \quad 0 \lt p \lt 1\)
- \(\left(-\infty, -\ln(\ln 4), -\ln(\ln 2), -\ln(\ln 4 - \ln 3), \infty\right)\)
- \(f(x) = e^{-e^{-x}} e^{-x}, \quad x \in \R\)
La distribución en el último ejercicio es la distribución de valor extremo tipo 1, también conocida como la distribución de Gumbel en honor a Emil Gumbel. Las distribuciones de valores extremos se estudian en detalle en el capítulo sobre Distribuciones especiales.
En la calculadora de distribución especial, seleccione la distribución de valores extremos y mantenga los valores de los parámetros predeterminados. Observe la forma y ubicación de la función de densidad de probabilidad y la función de distribución.
La distribución normal estándar
Recordemos que la distribución normal estándar tiene función de densidad de probabilidad\( \phi \) dada por\[ \phi(z) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2} z^2}, \quad z \in \R\] Esta distribución modela mediciones físicas de todo tipo sujetas a pequeños errores aleatorios, y es una de las distribuciones más importantes en probabilidad. La distribución normal se estudia con más detalle en el capítulo sobre Distribuciones Especiales. La función de distribución\( \Phi \), por supuesto, se puede expresar como\[ \Phi(z) = \int_{-\infty}^z \phi(x) \, dx, \quad z \in \R \] pero\( \Phi \) y la función cuantil\( \Phi^{-1} \) no se puede expresar, en cerrado desde, en términos de funciones elementales. Debido a la importancia de la distribución normal\( \Phi \) y\( \Phi^{-1} \) se consideran en sí mismas funciones especiales\( \sin \), como\( \ln \), y muchas otras. Los valores aproximados de estas funciones se pueden calcular utilizando la mayoría de los paquetes de software matemáticos y estadísticos. Debido a que la distribución es simétrica alrededor de 0,\( \Phi(-z) = 1 - \Phi(z) \) para\( z \in \R \), y equivalentemente,\( \Phi^{-1}(1 - p) = -\Phi^{-1}(p)\). En particular, la mediana es 0.
Abra la calculadora de distribución sepcial y elija la distribución normal. Mantenga los valores de los parámetros predeterminados y seleccione la vista CDF. Anote la forma y ubicación de la función de distribución/cuantil. Calculo cada uno de los siguientes:
- El primer y tercer cuartiles
- Los cuantiles de orden 0.9 y 0.1
- Los cuantiles de orden 0.95 y 0.05
Ejercicios Misceláneos
Supongamos que\(X\) tiene función de densidad de probabilidad\(f(x) = -\ln x\) para\(0 \lt x \le 1\).
- Esbozar la gráfica de\(f\).
- Encuentra la función de distribución\(F\) y dibuja el gráfico.
- Encuentra\( \P\left(\frac{1}{3} \le X \le \frac{1}{2}\right) \).
Contestar
- \(F(x) = x - x \ln x, \quad 0 \lt x \lt 1\)
- \(\P(\frac{1}{3} \le X \le \frac{1}{2}) = \frac{1}{6} + \frac{1}{2} \ln 2 - \frac{1}{3} \ln 3\)
Supongamos que se rozan un par de dados justos y\((X_1, X_2)\) se registra la secuencia de puntuaciones.
- Encuentra la función de distribución de\(Y = X_1 + X_2\), la suma de las puntuaciones.
- Encuentra la función de distribución de\( V = \max \{X_1, X_2\} \), la puntuación máxima.
- Encuentra la función de distribución condicional de\(Y\) dado\(V = 5\).
Contestar
Las variables aleatorias son discretas, por lo que las CDF son funciones de paso, con saltos en los valores de las variables. Las siguientes tablas dan los valores de las CDF en los valores de las variables aleatorias.
-
\(y\) 2 3 4 5 6 7 8 9 10 11 12 \(\P(Y \le y)\) \(\frac{1}{36}\) \(\frac{3}{36}\) \(\frac{6}{36}\) \(\frac{10}{36}\) \(\frac{15}{36}\) \(\frac{21}{36}\) \(\frac{26}{36}\) \(\frac{30}{36}\) \(\frac{33}{36}\) \(\frac{35}{36}\) 1 -
\(v\) 1 2 3 4 5 6 \(\P(V \le v)\) \(\frac{1}{36}\) \(\frac{4}{36}\) \(\frac{9}{36}\) \(\frac{16}{36}\) \(\frac{25}{36}\) 1 -
\(y\) 6 7 8 9 10 \(\P(Y \le y \mid V = 5)\) \(\frac{2}{9}\) \(\frac{4}{9}\) \(\frac{6}{9}\) \(\frac{8}{9}\) 1
Supongamos que\((X, Y)\) tiene función de densidad de probabilidad\(f(x, y) = x + y\) para\(0 \le x \le 1\),\(0 \le y \le 1\).
- Encuentra la función de distribución de\(X, Y)\).
- \(\P\left(\frac{1}{4} \le X \le \frac{1}{2}, \frac{1}{3} \le Y \le \frac{2}{3}\right)\)Cómpiate.
- Encuentra la función de distribución de\(X\).
- Encuentra la función de distribución de\(Y\).
- Encuentra la función de distribución condicional de\(X\) dado\(Y = y\) para\(0 \lt y \lt 1 \).
- Encuentra la función de distribución condicional de\(Y\) dado\(X = x\) para\(0 \lt x \lt 1\).
- ¿Son\(X\) e\(Y\) independientes?
Contestar
- \(F(x, y) = \frac{1}{2}\left(x y^2 + y x^2\right); \quad 0 \lt x \lt 1, \; 0 \lt y \lt 1\)
- \(\P\left(\frac{1}{4} \le X \le \frac{1}{2}, \frac{1}{3} \le Y \le \frac{2}{3}\right) = \frac{7}{96}\)
- \(G(x) = \frac{1}{2}\left(x + x^2\right), \quad 0 \lt x \lt 1\)
- \(H(y) = \frac{1}{2}\left(y + y^2\right), \quad 0 \lt y \lt 1\)
- \(G(x \mid y) = \frac{x^2 / 2 + x y}{y + 1/2}; \quad 0 \lt x \lt 1, \; 0 \lt y \lt 1\)
- \(H(y \mid x) = \frac{y^2 / 2 + x y}{x + 1/2}; \quad 0 \lt x \lt 1, \; 0 \lt y \lt 1\)
Ejercicios Estadísticos
Para los datos de M&M, computar la función de distribución empírica del número total de caramelos.
Contestar
Dejar\(N\) denotar el número total de caramelos. La función de distribución empírica de\(N\) es una función de paso; la siguiente tabla da los valores de la función en los puntos de salto.
| \(n\) | 50 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(\P(N \le n)\) | \(\frac{1}{30}\) | \(\frac{2}{30}\) | \(\frac{3}{30}\) | \(\frac{7}{30}\) | \(\frac{11}{30}\) | \(\frac{14}{30}\) | \(\frac{23}{30}\) | \(\frac{26}{30}\) | \(\frac{28}{30}\) | 1 |
Para los datos de cigarra, let\(BL\) denota longitud corporal y let\(G\) denota género. Compute la función de distribución empírica de las siguientes variables:
- \(BL\)
- \(BL\)dado\(G = 1\) (masculino)
- \(BL\)dado\(G = 0\) (femenino).
- ¿Crees eso\(BL\) y\(G\) eres independiente?
Para las versiones estadísticas de algunos de los temas de esta sección, consulte el capítulo sobre Muestras Aleatorias, y en particular, las secciones sobre distribuciones empíricas y estadísticas de orden.


