4.3: Varianza
- Page ID
- 151943
Recordemos que el valor esperado de una variable aleatoria de valor real es la media de la variable, y es una medida del centro de la distribución. Recordemos también que al tomar el valor esperado de diversas transformaciones de la variable, podemos medir otras características interesantes de la distribución. En esta sección, estudiaremos los valores esperados que miden la dispersión de la distribución sobre la media.
Teoría Básica
Definiciones e interpretaciones
Como es habitual, comenzamos con un experimento aleatorio modelado por un espacio de probabilidad\((\Omega, \mathscr F, \P)\). Entonces, para revisar,\(\Omega\) es el conjunto de resultados,\(\mathscr F\) la recolección de eventos, y\(\P\) la medida de probabilidad en el espacio muestral\((\Omega, \mathscr F)\). Supongamos que\(X\) es una variable aleatoria para el experimento, tomando valores adentro\(S \subseteq \R\). Recordemos que\( \E(X) \), el valor esperado (o media) de\(X\) da el centro de la distribución de\(X\).
La varianza y desviación estándar de\( X \) se definen por
- \( \var(X) = \E\left(\left[X - \E(X)\right]^2\right) \)
- \( \sd(X) = \sqrt{\var(X)} \)
Implícita en la definición está la suposición de que la media\( \E(X) \) existe, como un número real. Si este no es el caso, entonces\( \var(X) \) (y por lo tanto también\( \sd(X) \)) están indefinidos. Aunque\( \E(X) \) exista como número real, es posible que\( \var(X) = \infty \). Para lo que resta de nuestra discusión de la teoría básica, asumiremos que los valores esperados que se mencionan existen como números reales.
La varianza y desviación estándar de\(X\) son ambas medidas de la dispersión de la distribución sobre la media. La varianza (como veremos) tiene propiedades matemáticas más agradables, pero su unidad física es el cuadrado de la de\( X \). La desviación estándar, en cambio, no es tan agradable matemáticamente, sino que tiene la ventaja de que su unidad física es la misma que la de\( X \). Cuando\(X\) se entiende la variable aleatoria, la desviación estándar a menudo se denota por\(\sigma\), de manera que la varianza es\(\sigma^2\).
Recordemos que el segundo momento de\(X\) aproximadamente\(a \in \R\) es\(\E\left[(X - a)^2\right]\). Así, la varianza es el segundo momento de\(X\) aproximadamente la media\(\mu = \E(X)\), o equivalentemente, el segundo momento central de\(X\). En general, el segundo momento de\( X \) aproximadamente también\( a \in \R\) puede pensarse como el error cuadrático medio si\( a \) se utiliza la constante como estimación de\( X \). Además, los segundos momentos tienen una agradable interpretación en física. Si pensamos en la distribución de\(X\) como una distribución masiva en\(\R\), entonces el segundo momento de\(X\) aproximadamente\(a \in \R\) es el momento de inercia de la distribución masiva alrededor\(a\). Esta es una medida de la resistencia de la distribución de masa a cualquier cambio en su movimiento de rotación alrededor\(a\). En particular, la varianza de\(X\) es el momento de inercia de la distribución de masa alrededor del centro de masa\(\mu\).

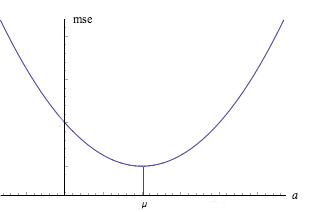
El error cuadrático medio (o equivalentemente el momento de inercia) aproximadamente\( a \) se minimiza cuando\( a = \mu \):
Dejemos\( \mse(a) = \E\left[(X - a)^2\right] \) para\( a \in \R \). Entonces\( \mse \) se minimiza cuando\( a = \mu \), y el valor mínimo es\( \sigma^2 \).
Prueba
La relación entre medidas de centro y medidas de propagación se estudia con más detalle en la sección avanzada sobre espacios vectoriales de variables aleatorias.
Propiedades
Los siguientes ejercicios dan algunas propiedades básicas de varianza, que a su vez se basan en propiedades básicas de valor esperado. Como es habitual, asegúrate de probar las pruebas tú mismo antes de leer las que aparecen en el texto. Nuestros primeros resultados son fórmulas computacionales basadas en el cambio de variables fórmula para el valor esperado
Vamos\( \mu = \E(X) \).
- Si\(X\) tiene una distribución discreta con función de densidad de probabilidad\(f\), entonces\( \var(X) = \sum_{x \in S} (x - \mu)^2 f(x) \).
- Si\(X\) tiene una distribución continua con función de densidad de probabilidad\(f\), entonces\( \var(X) = \int_S (x - \mu)^2 f(x) dx \)
Prueba
- Esto se desprende de la versión discreta de la fórmula de cambio de variables.
- De igual manera, esto se desprende de la versión continua de la fórmula de cambio de variables.
Nuestro siguiente resultado es una fórmula de varianza que suele ser mejor que la definición para fines computacionales.
\(\var(X) = \E(X^2) - [\E(X)]^2\).
Prueba
Vamos\( \mu = \E(X) \). Usando la linealidad del valor esperado tenemos\[ \var(X) = \E[(X - \mu)^2] = \E(X^2 - 2 \mu X + \mu^2) = \E(X^2) - 2 \mu \E(X) + \mu^2 = \E(X^2) - 2 \mu^2 + \mu^2 = \E(X^2) - \mu^2 \]
Por supuesto, por el cambio de variables fórmula,\( \E\left(X^2\right) = \sum_{x \in S} x^2 f(x) \) si\( X \) tiene una distribución discreta, y\( \E\left(X^2\right) = \int_S x^2 f(x) \, dx \) si\( X \) tiene una distribución continua. En ambos casos,\( f \) es la función de densidad de probabilidad de\( X \).
La varianza es siempre no negativa, ya que es el valor esperado de una variable aleatoria no negativa. Además, cualquier variable aleatoria que realmente sea aleatoria (no una constante) tendrá varianza estrictamente positiva.
La propiedad no negativa.
- \(\var(X) \ge 0\)
- \(\var(X) = 0\)si y sólo si\(\P(X = c) = 1\) por alguna constante\(c\) (y luego por supuesto,\(\E(X) = c\)).
Prueba
Estos resultados se derivan de la propiedad positiva básica de valor esperado. Vamos\( \mu = \E(X) \). Primero\( (X - \mu)^2 \ge 0 \) con probabilidad 1 así\( \E\left[(X - \mu)^2\right] \ge 0 \). Además,\( \E\left[(X - \mu)^2\right] = 0 \) si y sólo si\( \P(X = \mu) = 1 \).
Nuestro siguiente resultado muestra cómo la varianza y la desviación estándar son cambiadas por una transformación lineal de la variable aleatoria. En particular, tenga en cuenta que la varianza, a diferencia del valor general esperado, no es una operación lineal. Esto no es realmente sorprendente ya que la varianza es el valor esperado de una función no lineal de la variable:\( x \mapsto (x - \mu)^2 \).
Si\(a, \, b \in \R\) entonces
- \(\var(a + b X) = b^2 \var(X)\)
- \(\sd(a + b X) = \left|b\right| \sd(X)\)
Prueba
- Vamos\( \mu = \E(X) \). Por linealidad,\( \E(a + b X) = a + b \mu \). De ahí\( \var(a + b X) = \E\left([(a + b X) - (a + b \mu)]^2\right) = \E\left[b^2 (X - \mu)^2\right] = b^2 \var(X) \).
- Este resultado se desprende de (a) tomando raíces cuadradas.
Recordemos que cuando\( b \gt 0 \), la transformación lineal\( x \mapsto a + b x \) se denomina transformación de ubicación-escala y a menudo corresponde a un cambio de ubicación y cambio de escala en las unidades físicas. Por ejemplo, el cambio de pulgadas a centímetros en una medida de longitud es una transformación de escala, y el cambio de Fahrenheit a Celsius en una medición de temperatura es tanto una ubicación como una transformación de escala. El resultado anterior muestra que cuando se aplica una transformación ubicación-escala a una variable aleatoria, la desviación estándar no depende del parámetro de ubicación, sino que se multiplica por el factor de escala. Hay una transformación particularmente importante a escala de ubicación.
Supongamos que\( X \) es una variable aleatoria con media\( \mu \) y varianza\( \sigma^2 \). La variable aleatoria\( Z\) definida de la siguiente manera es la puntuación estándar de\( X \). \[ Z = \frac{X - \mu}{\sigma} \]
- \( \E(Z) = 0 \)
- \( \var(Z) = 1 \)
Prueba
- A partir de la linealidad del valor esperado,\( \E(Z) = \frac{1}{\sigma} [\E(X) - \mu] = 0 \)
- De la propiedad de escalado,\( \var(Z) = \frac{1}{\sigma^2} \var(X) = 1 \).
Dado que\(X\) y su media y desviación estándar tienen todas las mismas unidades físicas, la puntuación estándar\(Z\) es adimensional. Mide la distancia dirigida de\(\E(X)\) a\(X\) en términos de desviaciones estándar.
Vamos a\( Z \) denotar la puntuación estándar de\( X \), y supongamos que\( Y = a + b X \) donde\( a, \, b \in \R \) y\( b \ne 0 \).
- Si\( b \gt 0 \), la puntuación estándar de\( Y \) es\( Z \).
- Si\( b \lt 0 \), la puntuación estándar de\( Y \) es\( -Z \).
Prueba
\( E(Y) = a + b \E(X) \)y\( \sd(Y) = \left|b\right| \, \sd(X) \). De ahí\[ \frac{Y - \E(Y)}{\sd(Y)} = \frac{b}{\left|b\right|} \frac{X - \E(X)}{\sd(X)} \]
Como se acaba de señalar, cuando\( b \gt 0 \), la variable\(Y = a + b X \) es una transformación a escala de ubicación y a menudo corresponde a un cambio de unidades físicas. Dado que la puntuación estándar es adimensional, es razonable que las puntuaciones estándar de\( X \) y\( Y \) sean las mismas. Aquí hay otra medida estandarizada de dispersión:
Supongamos que\(X\) es una variable aleatoria con\(\E(X) \ne 0\). El coeficiente de variación es la relación entre la desviación estándar y la media:\[ \text{cv}(X) = \frac{\sd(X)}{\E(X)} \]
El coeficiente de variación también es adimensional, y a veces se utiliza para comparar la variabilidad de variables aleatorias con diferentes medias. Aprenderemos a calcular la varianza de la suma de dos variables aleatorias en la sección sobre covarianza.
Desigualdad de Chebyshev
La desigualdad de Chebyshev (llamada así por Pafnuty Chebyshev) da un límite superior sobre la probabilidad de que una variable aleatoria sea más de una distancia especificada de su media. Esto suele ser útil en problemas aplicados donde se desconoce la distribución, pero se conocen la media y varianza (al menos aproximadamente). En los dos resultados siguientes, supongamos que\(X\) es una variable aleatoria de valor real con media\(\mu = \E(X) \in \R\) y desviación estándar\(\sigma = \sd(X) \in (0, \infty)\).
La desigualdad de Chebyshev 1. \[ \P\left(\left|X - \mu\right| \ge t\right) \le \frac{\sigma^2}{t^2}, \quad t \gt 0 \]
Prueba
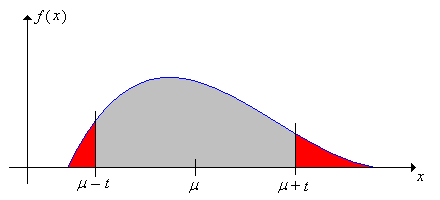
Aquí hay una versión alternativa, con la distancia en términos de desviación estándar.
La desigualdad de Chebyshev 2. \[\P\left(\left|X - \mu\right| \ge k \sigma\right) \le \frac{1}{k^2}, \quad k \gt 0 \]
Prueba
Dejemos\( t = k \sigma \) entrar la primera versión de la desigualdad de Chebyshev.
La utilidad de la desigualdad Chebyshev proviene del hecho de que se sostiene para cualquier distribución (asumiendo solo que la media y la varianza existen). La compensación es que para muchas distribuciones específicas, el encuadernado de Chebyshev es bastante crudo. Obsérvese en particular que la primera desigualdad es inútil cuando\(t \le \sigma\), y la segunda desigualdad es inútil cuando\( k \le 1 \), ya que 1 es un límite superior para la probabilidad de cualquier evento. Por otro lado, es fácil construir una distribución para la cual la desigualdad de Chebyshev es aguda para un valor específico de\( t \in (0, \infty) \). Dicha distribución se da en un ejercicio a continuación.
Ejemplos y Aplicaciones
Como siempre, asegúrate de probar los problemas tú mismo antes de mirar las soluciones y respuestas.
Variables de indicador
Supongamos que\(X\) es una variable indicadora con\(p = \P(X = 1)\), donde\(p \in [0, 1]\). Entonces
- \(\E(X) = p\)
- \(\var(X) = p (1 - p)\)
Prueba
- Esto lo demostramos en el apartado de propiedades básicas, aunque el resultado es tan sencillo que podemos volver a hacerlo:\( \E(X) = 1 \cdot p + 0 \cdot (1 - p) = p \).
- Tenga en cuenta que\( X^2 = X \) ya que\( X \) solo toma valores 0 y 1. De ahí\( \E\left(X^2\right) = p \) y por lo tanto\( \var(X) = p - p^2 = p (1 - p) \).
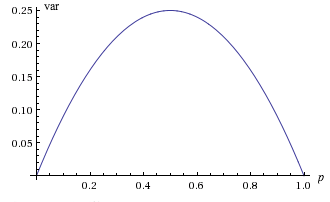
La gráfica de\(\var(X)\) como función de\(p\) es una parábola, que se abre hacia abajo, con raíces en 0 y 1. Así el valor mínimo de\(\var(X)\) es 0, y ocurre cuando\(p = 0\) y\(p = 1\) (cuando\( X \) es determinista, por supuesto). El valor máximo es\(\frac{1}{4}\) y ocurre cuando\(p = \frac{1}{2}\).
Distribuciones Uniformes
Las distribuciones discretas uniformes son ampliamente utilizadas en la probabilidad combinatoria, y modelan un punto elegido al azar de un conjunto finito. La media y la varianza tienen formas simples para la distribución uniforme discreta en un conjunto de puntos uniformemente espaciados (a veces denominados intervalo discreto):
Supongamos que\(X\) tiene la distribución uniforme discreta sobre\(\{a, a + h, \ldots, a + (n - 1) h\}\) dónde\( a \in \R \),\( h \in (0, \infty) \), y\( n \in \N_+ \). Vamos\( b = a + (n - 1) h \), el punto final correcto. Entonces
- \(\E(X) = \frac{1}{2}(a + b)\).
- \(\var(X) = \frac{1}{12}(b - a)(b - a + 2 h)\).
Prueba
- Esto lo demostramos en la sección de propiedades básicas. Aquí está nuevamente, usando la fórmula para la suma de los primeros enteros\( n - 1 \) positivos:\[ \E(X) = \frac{1}{n} \sum_{i=0}^{n-1} (a + i h) = \frac{1}{n}\left(n a + h \frac{(n - 1) n}{2}\right) = a + \frac{(n - 1) h}{2} = \frac{a + b}{2} \]
- Tenga en cuenta que\[ \E\left(X^2\right) = \frac{1}{n} \sum_{i=0}^{n-1} (a + i h)^2 = \frac{1}{n - 1} \sum_{i=0}^{n-1} \left(a^2 + 2 a h i + h^2 i^2\right)\] Usando las fórmulas para la suma de los primeros enteros\( n - 1 \) positivos, y la suma de los cuadrados de los primeros enteros\( n - 1 \) positivos, tenemos\[ \E\left(X^2\right) = \frac{1}{n}\left[ n a^2 + 2 a h \frac{(n-1) n}{2} + h^2 \frac{(n - 1) n (2 n -1)}{6}\right] \] Usando fórmula computacional y simplificando da el resultado.
Tenga en cuenta que la media es simplemente la media de los puntos finales, mientras que la varianza depende únicamente de la diferencia entre los puntos finales y el tamaño del paso.
Abra el simulador de distribución especial y seleccione la distribución uniforme discreta. Varíe los parámetros y anote la ubicación y el tamaño de la barra de desviación\(\pm\) estándar media en relación con la función de densidad de probabilidad. Para valores seleccionados de los parámetros, ejecute la simulación 1000 veces y compare la media empírica y la desviación estándar con la media de distribución y la desviación estándar.
A continuación, recordemos que la distribución uniforme continua en un intervalo acotado corresponde a seleccionar un punto al azar del intervalo. Las distribuciones uniformes continuas surgen en probabilidad geométrica y una variedad de otros problemas aplicados.
Supongamos que\(X\) tiene la distribución uniforme continua en el intervalo\([a, b]\) donde\( a, \, b \in \R \) con\( a \lt b \). Entonces
- \( \E(X) = \frac{1}{2}(a + b) \)
- \( \var(X) = \frac{1}{12}(b - a)^2 \)
Prueba
- \( \E(X) = \int_a^b x \frac{1}{b - a} \, dx = \frac{b^2 - a^2}{2 (b - a)} = \frac{a + b}{2} \)
- \( \E(X^2) = \int_a^b x^2 \frac{1}{b - a} = \frac{b^3 - a^3}{3 (b - a)} \). El resultado de varianza se deriva entonces de (a), la fórmula computacional y el álgebra simple.
Tenga en cuenta que la media es el punto medio del intervalo y la varianza depende únicamente de la longitud del intervalo. Compare esto con los resultados en el caso discreto.
Abra el simulador de distribución especial y seleccione la distribución uniforme continua. Esta es la distribución uniforme del intervalo\( [a, a + w] \). Varíe los parámetros y anote la ubicación y el tamaño de la barra de desviación\(\pm\) estándar media en relación con la función de densidad de probabilidad. Para valores seleccionados de los parámetros, ejecute la simulación 1000 veces y compare la media empírica y la desviación estándar con la media de distribución y la desviación estándar.
Dados
Recordemos que un dado justo es aquel en el que las caras son igualmente probables. Además de los dados justos, existen varios tipos de dados torcidos. Aquí hay tres:
- Un dado plano ace-seis es un dado de seis lados en el que las caras 1 y 6 tienen probabilidad\(\frac{1}{4}\) cada una mientras que las caras 2, 3, 4 y 5 tienen probabilidad\(\frac{1}{8}\) cada una.
- Un dado plano de dos y cinco es un dado de seis lados en el que las caras 2 y 5 tienen probabilidad\(\frac{1}{4}\) cada una mientras que las caras 1, 3, 4 y 6 tienen probabilidad\(\frac{1}{8}\) cada una.
- Un troquel plano de tres y cuatro es un dado de seis lados en el que las caras 3 y 4 tienen probabilidad\(\frac{1}{4}\) cada una mientras que las caras 1, 2, 5 y 6 tienen probabilidad\(\frac{1}{8}\) cada una.
Un dado plano, como su nombre indica, es un dado que no es un cubo, sino que es más corto en una de las tres direcciones. Las probabilidades particulares que utilizamos (\( \frac{1}{4} \)y\( \frac{1}{8} \)) son ficticias, pero la propiedad esencial de una matriz plana es que las caras opuestas en el eje más corto tienen probabilidades ligeramente mayores que las otras cuatro caras. Los dados planos a veces son utilizados por los apostadores para hacer trampa. En los siguientes problemas, calcularás la media y varianza para cada uno de los distintos tipos de dados. Asegúrese de comparar los resultados.
Se lanza un dado estándar, justo y\(X\) se registra el puntaje. Esbozar el gráfico de la función de densidad de probabilidad y calcular cada uno de los siguientes:
- \(\E(X)\)
- \(\var(X)\)
Contestar
- \(\frac{7}{2}\)
- \(\frac{35}{12}\)
Se lanza un dado plano ace-seis y\(X\) se registra el marcador. Esbozar el gráfico de la función de densidad de probabilidad y calcular cada uno de los siguientes:
- \(\E(X)\)
- \(\var(X)\)
Contestar
- \(\frac{7}{2}\)
- \(\frac{15}{4}\)
Se lanza un dado plano de dos-cinco y\(X\) se registra el marcador. Esbozar el gráfico de la función de densidad de probabilidad y calcular cada uno de los siguientes:
- \(\E(X)\)
- \(\var(X)\)
Contestar
- \(\frac{7}{2}\)
- \(\frac{11}{4}\)
Se lanza un dado plano de tres-cuatro y\(X\) se registra el marcador. Esbozar el gráfico de la función de densidad de probabilidad y calcular cada uno de los siguientes:
- \(\E(X)\)
- \(\var(X)\)
Contestar
- \(\frac{7}{2}\)
- \(\frac{9}{4}\)
En el experimento de dados, seleccione un dado. Para cada uno de los siguientes casos, anote la ubicación y el tamaño de la barra de desviación\(\pm\) estándar media en relación con la función de densidad de probabilidad. Ejecutar el experimento 1000 veces y comparar la media empírica y la desviación estándar con la media de distribución y desviación estándar.
- Muere justo
- Troquel plano Ace-seis
- Troquel plano de dos y cinco
- Troquel plano de tres y cuatro
La distribución de Poisson
Recordemos que la distribución de Poisson es una distribución discreta\( \N \) con función de densidad de probabilidad\( f \) dada por\[ f(n) = e^{-a} \, \frac{a^n}{n!}, \quad n \in \N\] donde\(a \in (0, \infty)\) es un parámetro. La distribución de Poisson lleva el nombre de Simeon Poisson y es ampliamente utilizada para modelar el número de puntos aleatorios
en una región de tiempo o espacio; el parámetro\(a\) es proporcional al tamaño de la región. La distribución de Poisson se estudia en detalle en el capítulo sobre el Proceso de Poisson.
Supongamos que\(N\) tiene la distribución de Poisson con parámetro\(a\). Entonces
- \(\E(N) = a\)
- \(\var(N) = a\)
Prueba
- Hicimos este cómputo en la sección anterior. Aquí está otra vez:\[ \E(N) = \sum_{n=0}^\infty n e^{-a} \frac{a^n}{n!} = e^{-a} \sum_{n=1}^\infty \frac{a^n}{(n - 1)!} = e^{-a} a \sum_{n=1}^\infty \frac{a^{n-1}}{(n-1)!} = e^{-a} a e^a = a.\]
- Primero calculamos el segundo momento factorial:\[ \E[N (N - 1)] = \sum_{n=1}^\infty n (n - 1) e^{-a} \frac{a^n}{n!} = \sum_{n=2}^\infty e^{-a} \frac{a^n}{(n - 2)!} = e^{-a} a^2 \sum_{n=2}^\infty \frac{a^{n-2}}{(n - 2)!} = a^2 e^{-a} e^a = a^2\] Por lo tanto,\( E\left(N^2\right) = \E[N(N - 1)] + \E(N) = a^2 + a \) y así\( \var(N) = (a^2 + a) - a^2 = a \).
Así, el parámetro de la distribución de Poisson es tanto la media como la varianza de la distribución.
En el experimento de Poisson, el parámetro es\(a = r t\). Varíe el parámetro y anote el tamaño y la ubicación de la barra de desviación\(\pm\) estándar media en relación con la función de densidad de probabilidad. Para los valores seleccionados del parámetro, ejecute el experimento 1000 veces y compare la media empírica y la desviación estándar con la media de distribución y la desviación estándar.
La distribución geométrica
Recordemos que los ensayos de Bernoulli son ensayos independientes cada uno con dos resultados, que en el lenguaje de la confiabilidad, se llaman éxito y fracaso. La probabilidad de éxito en cada ensayo es\( p \in [0, 1] \). Un capítulo separado sobre los ensayos de Bernoulli explora este proceso aleatorio con más detalle. Se llama así por Jacob Bernoulli. Si\( p \in (0, 1] \), el número\( N \) de prueba del primer éxito tiene la distribución geométrica\(\N_+\) con parámetro éxito\(p\). La función de densidad de probabilidad\( f \) de\( N \) viene dada por\[ f(n) = p (1 - p)^{n - 1}, \quad n \in \N_+ \]
Supongamos que\(N\) tiene la distribución geométrica\(\N_+\) encendida con parámetro de éxito\(p \in (0, 1]\). Entonces
- \(\E(N) = \frac{1}{p}\)
- \(\var(N) = \frac{1 - p}{p^2}\)
Prueba
- Esto lo demostramos en la sección de propiedades básicas. Aquí está otra vez:\[ \E(N) = \sum_{n=1}^\infty n p (1 - p)^{n-1} = -p \frac{d}{dp} \sum_{n=0}^\infty (1 - p)^n = -p \frac{d}{dp} \frac{1}{p} = p \frac{1}{p^2} = \frac{1}{p}\]
- Primero calculamos el segundo momento factorial:\[ \E[N(N - 1)] = \sum_{n = 2}^\infty n (n - 1) (1 - p)^{n-1} p = p(1 - p) \frac{d^2}{dp^2} \sum_{n=0}^\infty (1 - p)^n = p (1 - p) \frac{d^2}{dp^2} \frac{1}{p} = p (1 - p) \frac{2}{p^3} = \frac{2 (1 - p)}{p^2}\] De ahí\( \E(N^2) = \E[N(N - 1)] + \E(N) = 2 / p^2 - 1 / p \) y por lo tanto\( \var(X) = 2 / p^2 - 1 / p - 1 / p^2 = 1 / p^2 - 1 / p \).
Obsérvese que la varianza es 0 cuando\(p = 1\), no es sorprendente ya que\( X \) es determinista en este caso.
En el experimento binomial negativo, establecer\(k = 1\) para obtener la distribución geométrica. Varíe\(p\) con la barra de desplazamiento y anote el tamaño y la ubicación de la barra de desviación\(\pm\) estándar media en relación con la función de densidad de probabilidad. Para los valores seleccionados de\(p\), ejecute el experimento 1000 veces y compare la media empírica y la desviación estándar con la media de distribución y la desviación estándar.
Supongamos que\(N\) tiene la distribución geométrica con parámetro\(p = \frac{3}{4}\). Calcular el valor verdadero y el límite de Chebyshev para la probabilidad de que\(N\) esté al menos a 2 desviaciones estándar de la media.
Contestar
- \(\frac{1}{16}\)
- \(\frac{1}{4}\)
La distribución exponencial
Recordemos que la distribución exponencial es una distribución continua\( [0, \infty) \) con función de densidad de probabilidad\( f \) dada por\[ f(t) = r e^{-r t}, \quad t \in [0, \infty) \] donde\(r \in (0, \infty)\) es el parámetro with rate. Esta distribución es ampliamente utilizada para modelar tiempos de falla y otros tiempos de llegada
. La distribución exponencial se estudia en detalle en el capítulo sobre el Proceso de Poisson.
Supongamos que\(T\) tiene la distribución exponencial con parámetro rate\(r\). Entonces
- \(\E(T) = \frac{1}{r}\).
- \(\var(T) = \frac{1}{r^2}\).
Prueba
- Esto lo demostramos en la sección de propiedades básicas. Aquí está de nuevo, utilizando la integración por partes:\[ \E(T) = \int_0^\infty t r e^{-r t} \, dt = -t e^{-r t} \bigg|_0^\infty + \int_0^\infty e^{-r t} \, dt = 0 - \frac{1}{r} e^{-rt} \bigg|_0^\infty = \frac{1}{r} \]
- Integrando de nuevo por partes y usando (a), tenemos\[ \E\left(T^2\right) = \int_0^\infty t^2 r e^{-r t} \, dt = -t^2 e^{-r t} \bigg|_0^\infty + \int_0^\infty 2 t e^{-r t} \, dt = 0 + \frac{2}{r^2} \] Por lo tanto\( \var(T) = \frac{2}{r^2} - \frac{1}{r^2} = \frac{1}{r^2} \)
Así, para la distribución exponencial, la media y la desviación estándar son las mismas.
En el experimento gamma, configurado\(k = 1\) para obtener la distribución exponencial. Varíe\(r\) con la barra de desplazamiento y anote el tamaño y la ubicación de la barra de desviación\(\pm\) estándar media en relación con la función de densidad de probabilidad. Para los valores seleccionados de\(r\), ejecute el experimento 1000 veces y compare la media empírica y la desviación estándar con la media de distribución y la desviación estándar.
Supongamos que\(X\) tiene la distribución exponencial con parámetro rate\(r \gt 0\). Calcular el valor verdadero y el límite de Chebyshev para la probabilidad de que\(X\) esté al menos desviaciones\(k\) estándar alejadas de la media.
Contestar
- \(e^{-(k+1)}\)
- \(\frac{1}{k^2}\)
La distribución de Pareto
Recordemos que la distribución de Pareto es una distribución continua\( [1, \infty) \) con función de densidad de probabilidad\( f \) dada por\[ f(x) = \frac{a}{x^{a + 1}}, \quad x \in [1, \infty) \] donde\(a \in (0, \infty)\) es un parámetro. La distribución de Pareto lleva el nombre de Vilfredo Pareto. Se trata de una distribución de cola pesada que es ampliamente utilizada para modelar variables financieras como el ingreso. La distribución de Pareto se estudia en detalle en el capítulo sobre Distribuciones Especiales.
Supongamos que\(X\) tiene la distribución de Pareto con parámetro shape\(a\). Entonces
- \(\E(X) = \infty\)si\(0 \lt a \le 1\) y\(\E(X) = \frac{a}{a - 1}\) si\(1\lt a \lt \infty\)
- \(\var(X)\)no está definido\(\var(X) = \infty\) si\(0 \lt a \le 1\)\(1 \lt a \le 2\), si y\(\var(X) = \frac{a}{(a - 1)^2 (a - 2)}\) si\(2 \lt a \lt \infty\)
Prueba
- Esto lo demostramos en la sección de propiedades básicas. Aquí está otra vez:\[ \E(X) = \int_1^\infty x \frac{a}{x^{a+1}} \, dx = \int_1^\infty \frac{a}{x^a} \, dx = \frac{a}{-a + 1} x^{-a + 1} \bigg|_1^\infty = \begin{cases} \infty, & 0 \lt a \lt 1 \\ \frac{a}{a - 1}, & a \gt 1 \end{cases} \] Cuando\( a = 1 \),\( \E(X) = \int_1^\infty \frac{1}{x} = \ln x \bigg|_1^\infty = \infty \)
- Si\( 0 \lt a \le 1 \) entonces\( \E(X) = \infty \) y así\( \var(X) \) es indefinido. Por otro lado,\[ \E\left(X^2\right) = \int_1^\infty x^2 \frac{a}{x^{a+1}} \, dx = \int_1^\infty \frac{a}{x^{a-1}} \, dx = a x^{-a + 2} \bigg|_1^\infty = \begin{cases} \infty, & 0 \lt a \lt 2 \\ \frac{a}{a - 2}, & a \gt 2 \end{cases} \] Cuando\( a = 2 \),\( \E\left(X^2\right) = \int_1^\infty \frac{2}{x} \, dx = \infty \). De ahí\( \var(X) = \infty \) si\( 1 \lt a \le 2 \) y\( \var(X) = \frac{a}{a - 2} - \left(\frac{a}{a - 1}\right)^2 \) si\( a \gt 2 \).
En el simuador de distribución especial, seleccione la distribución de Pareto. Varíe\(a\) con la barra de desplazamiento y anote el tamaño y la ubicación de la barra de desviación\(\pm\) estándar media. Para cada uno de los siguientes valores de\(a\), ejecutar el experimento 1000 veces y anotar el comportamiento de la media empírica y desviación estándar.
- \(a = 1\)
- \(a = 2\)
- \(a = 3\)
La distribución normal
Recordemos que la distribución normal estándar es una distribución continua\( \R \) con función de densidad de probabilidad\( \phi \) dada por
\[ \phi(z) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2} z^2}, \quad z \in \R \]
Las distribuciones normales son ampliamente utilizadas para modelar mediciones físicas sujetas a pequeños errores aleatorios y se estudian en detalle en el capítulo sobre Distribuciones Especiales.
Supongamos que\(Z\) tiene la distribución normal estándar. Entonces
- \(\E(Z) = 0\)
- \(\var(Z) = 1\)
Prueba
- Esto lo demostramos en la sección de propiedades básicas. Aquí está otra vez:\[ \E(Z) = \int_{-\infty}^\infty z \frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2} z^2} \, dz = - \frac{1}{\sqrt{2 \pi}} e^{-\frac{1}{2} z^2} \bigg|_{-\infty}^\infty = 0 - 0 \]
- De (a),\( \var(Z) = \E(Z^2) = \int_{-\infty}^\infty z^2 \phi(z) \, dz \). Integrar por partes con\( u = z \) y\( dv = z \phi(z) \, dz \). Así,\( du = dz \) y\( v = -\phi(z) \). De ahí\[ \var(Z) = -z \phi(z) \bigg|_{-\infty}^\infty + \int_{-\infty}^\infty \phi(z) \, dz = 0 + 1 \]
Más generalmente, para\(\mu \in \R\) y\(\sigma \in (0, \infty)\), recordar que la distribución normal con parámetro de ubicación\(\mu\) y parámetro de escala\(\sigma\) es una distribución continua\( \R \) con función de densidad de probabilidad\( f \) dada por\[ f(x) = \frac{1}{\sqrt{2 \pi} \sigma} \exp\left[-\frac{1}{2}\left(\frac{x - \mu}{\sigma}\right)^2\right], \quad x \in \R \] Además, si \( Z \)tiene la distribución normal estándar, luego\( X = \mu + \sigma Z \) tiene la distribución normal con parámetro de ubicación\( \mu \) y parámetro de escala\( \sigma \). Como sugiere la notación, el parámetro de ubicación es la media de la distribución y el parámetro de escala es la desviación estándar.
Supongamos que\( X \) tiene la distribución normal con parámetro de ubicación\(\mu\) y parámetro de escala\(\sigma\). Entonces
- \(\E(X) = \mu\)
- \(\var(X) = \sigma^2\)
Prueba
Podríamos usar la función de densidad de probabilidad, por supuesto, pero es mucho mejor usar la representación de\( X \) en términos de la variable normal estándar\( Z \), y usar propiedades de valor esperado y varianza.
- \( \E(X) = \mu + \sigma \E(Z) = \mu + 0 = \mu \)
- \( \var(X) = \sigma^2 \var(Z) = \sigma^2 \cdot 1 = \sigma^2 \).
Entonces, para resumir, si\( X \) tiene una distribución normal, entonces su puntaje estándar\( Z \) tiene la distribución normal estándar.
En el simulador de distribución especial, seleccione la distribución normal. Varíe los parámetros y anote la forma y ubicación de la barra de desviación\(\pm\) estándar media en relación con la función de densidad de probabilidad. Para los valores de parámetros seleccionados, ejecute el experimento 1000 veces y compare la media empírica y la desviación estándar con la media de distribución y la desviación estándar.
Distribuciones Beta
Las distribuciones de esta subsección pertenecen a la familia de distribuciones beta, las cuales son ampliamente utilizadas para modelar proporciones y probabilidades aleatorias. La distribución beta se estudia en detalle en el capítulo sobre Distribuciones Especiales.
Supongamos que\(X\) tiene una distribución beta con función de densidad de probabilidad\(f\). En cada caso a continuación, grafica\(f\) a continuación y calcula la media y varianza.
- \(f(x) = 6 x (1 - x)\)para\(x \in [0, 1]\)
- \(f(x) = 12 x^2 (1 - x)\)para\(x \in [0, 1]\)
- \(f(x) = 12 x (1 - x)^2\)para\(x \in [0, 1]\)
Contestar
- \(\E(X) = \frac{1}{2}\),\(\var(X) = \frac{1}{20}\)
- \(\E(X) = \frac{3}{5}\),\(\var(X) = \frac{1}{25}\)
- \(\E(X) = \frac{2}{6}\),\(\var(X) = \frac{1}{25}\)
En el simulador de distribución especial, seleccione la distribución beta. Los valores de los parámetros a continuación dan las distribuciones en el ejercicio anterior. En cada caso, anote la ubicación y el tamaño de la barra de desviación\(\pm\) estándar media. Ejecutar el experimento 1000 veces y comparar la media empírica y la desviación estándar con la media de distribución y desviación estándar.
- \( a = 2 \),\( b = 2 \)
- \( a = 3 \),\( b = 2 \)
- \( a = 2 \),\( b = 3 \)
Supongamos que una esfera tiene un radio aleatorio\(R\) con función de densidad de probabilidad\(f\) dada por\(f(r) = 12 r ^2 (1 - r)\) for\(r \in [0, 1]\). Encuentra la media y desviación estándar de cada uno de los siguientes:
- La circunferencia\(C = 2 \pi R\)
- El área de superficie\(A = 4 \pi R^2\)
- El volumen\(V = \frac{4}{3} \pi R^3\)
Contestar
- \(\frac{6}{5} \pi\),\( \frac{2}{5} \pi \)
- \(\frac{8}{5} \pi\),\(\frac{2}{5} \sqrt{\frac{38}{7}} \pi\)
- \(\frac{8}{21} \pi\),\( \frac{8}{3} \sqrt{\frac{19}{1470}} \pi \)
Supongamos que\(X\) tiene función de densidad de probabilidad\(f\) dada por\(f(x) = \frac{1}{\pi \sqrt{x (1 - x)}}\) for\(x \in (0, 1)\). Encuentra
- \( \E(X) \)
- \( \var(X) \)
Contestar
- \(\frac{1}{2}\)
- \(\frac{1}{8}\)
La distribución beta particular en el último ejercicio también se conoce como la distribución (estándar) del arcoseno. Gobierna la última vez que el proceso de movimiento browniano alcanza 0 durante el intervalo de tiempo\( [0, 1] \). La distribución del arcoseno se estudia en mayor generalidad en el capítulo sobre Distribuciones Especiales.
Abre el experimento de movimiento browniano y selecciona el último cero. Anote la ubicación y el tamaño de la barra de desviación\( \pm \) estándar media en relación con la función de densidad de probabilidad. Ejecute la simulación 1000 veces y compare la media empírica y la desviación estándar con la media de distribución y la desviación estándar.
Supongamos que las calificaciones en una prueba son descritas por la variable aleatoria\( Y = 100 X \) donde\( X \) tiene la distribución beta con función de densidad de probabilidad\( f \) dada por\( f(x) = 12 x (1 - x)^2 \) for\( x \in [0, 1] \). Las calificaciones son generalmente bajas, por lo que el profesor decide curvar
las calificaciones usando la transformación\( Z = 10 \sqrt{Y} = 100 \sqrt{X}\). Encuentra la media y desviación estándar de cada una de las siguientes variables:
- \( X \)
- \( Y \)
- \( Z \)
Contestar
- \( \E(X) = \frac{2}{5} \),\( \sd(X) = \frac{1}{5} \)
- \( \E(Y) = 40 \),\( \sd(Y) = 20 \)
- \( \E(Z) = 60.95 \),\( \sd(Z) = 16.88 \)
Ejercicios sobre Propiedades Básicas
Supongamos que\(X\) es una variable aleatoria de valor real con\(\E(X) = 5\) y\(\var(X) = 4\). Encuentra cada uno de los siguientes:
- \(\var(3 X - 2)\)
- \(\E(X^2)\)
Contestar
- \(36\)
- \(29\)
Supongamos que\(X\) es una variable aleatoria de valor real con\(\E(X) = 2\) y\(\E\left[X(X - 1)\right] = 8\). Encuentra cada uno de los siguientes:
- \(\E(X^2)\)
- \(\var(X)\)
Contestar
- \(10\)
- \(6\)
El valor esperado\(\E\left[X(X - 1)\right]\) es un ejemplo de un momento factorial.
Supongamos que\(X_1\) y\(X_2\) son variables aleatorias independientes, de valor real con\(\E(X_i) = \mu_i\) y\(\var(X_i) = \sigma_i^2\) para\(i \in \{1, 2\}\). Entonces
- \( \E\left(X_1 X_2\right) = \mu_1 \mu_2 \)
- \( \var\left(X_1 X_2\right) = \sigma_1^2 \sigma_2^2 + \sigma_1^2 \mu_2^2 + \sigma_2^2 \mu_1^2\)
Prueba
- Este es un resultado importante y básico que se comprobó en el apartado de propiedades básicas.
- Desde\( X_1^2 \) y también\( X_2^2 \) somos independientes, tenemos\(\E\left(X_1^2 X_2^2\right) = \E\left(X_1^2\right) \E\left(X_2^2\right) = (\sigma_1^2 + \mu_1^2) (\sigma_2^2 + \mu_2^2) \). El resultado se desprende entonces de la fórmula computacional y álgebra.
Marilyn Vos Savant tiene un coeficiente intelectual de 228. Suponiendo que la distribución de los puntajes de CI tiene media 100 y desviación estándar 15, encuentre la puntuación estándar de Marilyn.
Contestar
\(z = 8.53\)
Arreglar\( t \in (0, \infty) \). Supongamos que\( X \) es la variable aleatoria discreta con función de densidad de probabilidad definida por\( \P(X = t) = \P(X = -t) = p \),\( \P(X = 0) = 1 - 2 p \), donde\( p \in (0, \frac{1}{2}) \). Entonces la igualdad se sostiene en la desigualdad de Chebyshev en\( t \).
Prueba
Tenga en cuenta que\( \E(X) = 0 \) y\( \var(X) = \E(X^2) = 2 p t^2 \). Entonces\( \P(|X| \ge t) = 2 p \) y\( \sigma^2 / t^2 = 2 p \).


