6.7: Correlación muestral y regresión
- Page ID
- 152194
Teoría Descriptiva
Recordemos el modelo básico de estadística: tenemos una población de objetos de interés, y tenemos diversas medidas (variables) que hacemos sobre estos objetos. Seleccionamos objetos de la población y registramos las variables para los objetos de la muestra; estas se convierten en nuestros datos. Nuestra primera discusión es desde un punto de vista puramente descriptivo. Es decir, no asumimos que los datos son generados por una distribución de probabilidad subyacente. Pero como siempre, recuerde que los propios datos definen una distribución de probabilidad, es decir, la distribución empírica que asigna igual probabilidad a cada punto de datos.
Supongamos que\(x\) y\(y\) son variables de valor real para una población, y que\(\left((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\right)\) es una muestra observada de tamaño\(n\) de\((x, y)\). Vamos a dejar\(\bs{x} = (x_1, x_2, \ldots, x_n)\) denotar la muestra de\(x\) y\(\bs{y} = (y_1, y_2, \ldots, y_n)\) la muestra de\(y\). En esta sección, nos interesan las estadísticas que son medidas de asociación entre los\(\bs{x}\) y\(\bs{y}\), y en encontrar la línea (u otra curva) que mejor se ajuste a los datos.
Recordemos que las medias de la muestra son\[ m(\bs{x}) = \frac{1}{n} \sum_{i=1}^n x_i, \quad m(\bs{y}) = \frac{1}{n} \sum_{i=1}^n y_i \] y las varianzas de la muestra son\[ s^2(\bs{x}) = \frac{1}{n - 1} \sum_{i=1}^n [x_i - m(\bs{x})]^2, \quad s^2(\bs{y}) = \frac{1}{n - 1} \sum_{i=1}^n [y_i - m(\bs{y})]^2 \]
Gráficas de dispersión
A menudo, el primer paso en el análisis exploratorio de datos es dibujar una gráfica de los puntos; esto se llama diagrama de dispersión y puede dar un sentido visual de la relación estadística entre las variables.
En particular, nos interesa si la nube de puntos parece mostrar una tendencia lineal o si alguna curva no lineal podría ajustarse a la nube de puntos. Estamos interesados en la medida en que una variable\(x\) puede ser utilizada para predecir la otra variable\(y\).
Definciones
Nuestro siguiente objetivo es definir estadísticas que midan la asociación entre los\(y\) datos\(x\) y.
La covarianza de la muestra se define como\[ s(\bs{x}, \bs{y}) = \frac{1}{n - 1} \sum_{i=1}^n [x_i - m(\bs{x})][y_i - m(\bs{y})] \] Suponiendo que los vectores de datos no son constantes, de manera que las desviaciones estándar son positivas, la correlación de la muestra se define como\[ r(\bs{x}, \bs{y}) = \frac{s(\bs{x}, \bs{y})}{s(\bs{x}) s(\bs{y})} \]
Obsérvese que la covarianza muestral es un promedio del producto de las desviaciones de los\(y\) datos\(x\) y de sus medias. Así, la unidad física de la covarianza muestral es el producto de las unidades de\( x \) y\( y \). La correlación es una versión estandarizada de la covarianza. En particular, la correlación es adimensional (no tiene unidades físicas), ya que la covarianza en el numerador y el producto de las devaciones estándar en el denominador tienen las mismas unidades (el producto de las unidades de\(x\) y\(y\)). Obsérvese también que la covarianza y correlación tienen el mismo signo: positivo, negativo o cero. En el primer caso,\(\bs{y}\) se dice que los datos\(\bs{x}\) y están correlacionados positivamente; en el segundo caso\(\bs{x}\) y\(\bs{y}\) se dice que están correlacionados negativamente; y en el tercer caso\(\bs{x}\) y\(\bs{y}\) se dice que no están correlacionados
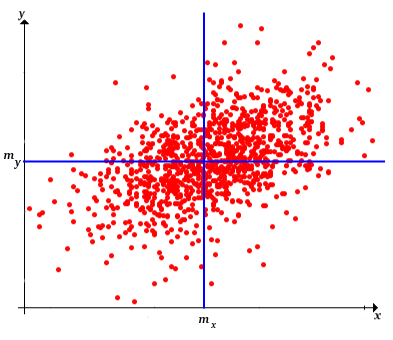
Para ver que la covarianza muestral es una medida de asociación, recordemos primero que el punto\(\left(m(\bs{x}), m(\bs{y})\right)\) es una medida del centro de los datos bivariados. En efecto, si cada punto es la ubicación de una masa unitaria, entonces\(\left(m(\bs{x}), m(\bs{y})\right)\) es el centro de masa como se define en la física. Las líneas horizontales y verticales a través de este punto central dividen el plano en cuatro cuadrantes. La desviación del producto\([x_i - m(\bs{x})][y_i - m(\bs{y})]\) es positiva en el primer y tercer cuadrantes y negativa en el segundo y cuarto cuadrantes. Después de estudiar la regresión lineal a continuación, tendremos un sentido mucho más profundo de lo que mide la covarianza.
Puede estar perplejo de que promediemos las desviaciones del producto dividiendo por\(n - 1\) en lugar de\(n\). La mejor explicación es que en el modelo de probabilidad que se analiza a continuación, la covarianza muestral es un estimador imparcial de la covarianza de distribución. Sin embargo, el modo de promediar también se puede entender en términos de grados de libertad, como se hizo para la varianza muestral. Inicialmente, tenemos\(2 n\) grados de libertad en los datos bivariados. Perdemos dos por el cálculo de las medias muestrales\(m(\bs{x})\) y\(m(\bs{y})\). De los restantes\(2 n - 2\) grados de libertad, perdemos\(n - 1\) calculando las desviaciones del producto. Así, nos quedamos con\(n - 1\) grados de libertad total. Como es típico en la estadística, promediamos no dividiendo por el número de términos en la suma sino por el número de grados de libertad en esos términos. No obstante, desde un punto de vista puramente descriptivo, también sería razonable dividir por\(n\).
Recordemos que existe una distribución natural de probabilidad asociada a los datos, es decir, la distribución empírica que da probabilidad\(\frac{1}{n}\) a cada punto de datos\((x_i, y_i)\). (Así, si estos puntos son distintos esta es la distribución uniforme discreta en los datos.) Las medias muestrales son simplemente los valores esperados de esta distribución bivariada, y a excepción de un múltiplo constante (dividiendo por\(n - 1\) en lugar de\(n\)), las varianzas de la muestra son simplemente las varianzas de esta distribución de bivarita. De manera similar, excepto por un múltiplo constante (dividiendo de nuevo por\(n - 1\) más que\(n\)), la covarianza muestral es la covarianza de la distribución bivariada y la correlación muestral es la correlación de la distribución bivariada. Todos los siguientes resultados en nuestra discusión de la estadística descriptiva son en realidad casos especiales de resultados más generales para distribuciones de probabilidad.
Propiedades de Covarianza
Los siguientes ejercicios establecen algunas propiedades esenciales de la covarianza muestral. Como es habitual, los símbolos en negrita denotan muestras de un tamaño fijo\(n\) de las variables poblacionales correspondientes (es decir, vectores de longitud\(n\)), mientras que los símbolos de tipo regular denotan números reales. Nuestro primer resultado es una fórmula para la covarianza muestral que a veces es mejor que la definición para fines computacionales. Para exponer el resultado de manera sucinta, vamos a\(\bs{x} \bs{y} = (x_1 \, y_1, x_2 \, y_2, \ldots, x_n \, y_n)\) denotar la muestra de la variable producto\(x y\).
La covarianza de la muestra se puede calcular de la siguiente manera:\[ s(\bs{x}, \bs{y}) = \frac{1}{n - 1} \sum_{i=1}^n x_i \, y_i - \frac{n}{n - 1} m(\bs{x}) m(\bs{y}) = \frac{n}{n - 1} [m(\bs{x y}) - m(\bs{x}) m(\bs{y})] \]
Prueba
Tenga en cuenta que\ begin {align}\ sum_ {i=1} ^n [(x_i - m (\ bs {x})] [y_i - m (\ bs {y})] & =\ sum_ {i=1} ^n [x_i y_i - x_i m (\ bs {y}) - y_i m (\ bs {x}) + m (\ bs {x}) m (\ bs {y})]\\ & =\ suma_ {i=1} ^n x_i y_i - m (\ bs {y})\ suma_ {i=1} ^n x_i - m (\ bs {x})\ suma_ {i=1} ^n y_i + n m (\ bs {x}) m (\ bs {y})\\ & =\ sum_ {i=1 =1} ^n x_i y_i - n m (\ bs { y}) m (\ bs {x}) - n m (\ bs {x}) m (\ bs {y}) + n m (\ bs {x}) m (\ bs {y})\\ & =\ suma_ {i=1} ^n x_i y_i - n m (\ bs {x}) m (\ bs {y})\ end align {}
El siguiente teorema da otra fórmula para la covarianza muestral, una que no requiere el cálculo de estadísticas intermedias.
La covarianza de la muestra se puede calcular de la siguiente manera:\[ s(\bs{x}, \bs{y}) = \frac{1}{2 n (n - 1)} \sum_{i=1}^n \sum_{j=1}^n (x_i - x_j)(y_i - y_j) \]
Prueba
Tenga en cuenta que\ begin {align}\ suma_ {i=1} ^n\ suma_ {j=1} ^n (x_i - x_j) (y_i - y_j) & =\ frac {1} {2 n}\ suma_ {i=1} ^n\ suma_ {j=1} ^n [x_i - m (\ bs {x}) + m (\ bs {x}) - x_j] [y_i - m (\ bs {y}) + m (\ bs {y}) - y_j]\\ & =\ sum_ {i=1} ^n\ suma_ {j=1} ^n\ izquierda ([(x_i - m (\ bs {x})] [y_i - m (\ bs {y})] + [x_i - m (\ bs {x})] [m (\ bs {y}) - y_j] + [m (\ bs {x}) - x_j] [y_i - m (\ bs {y})] + [m (\ bs {x}) - x_j] [m (\ bs {y}) - y_j]\ derecha)\ end {align} Calculamos las sumas término por término. El primero es\[n \sum_{i=1}^n [x_i - m(\bs{x})][y_i - m(\bs{y})]\] El segundo dos sumas son 0. La última suma es\[n \sum_{j=1}^n [m(\bs{x}) - x_j][m(\bs{y}) - y_j] = n \sum_{i=1}^n [x_i - m(\bs{x})][y_i - m(\bs{y})]\] Dividiendo la suma total por\(2 n (n - 1)\) resultados en\(\cov(\bs{x}, \bs{y})\).
Como su nombre indica, la covarianza muestral generaliza la varianza muestral.
\(s(\bs{x}, \bs{x}) = s^2(\bs{x})\).
A la luz del teorema anterior, ahora podemos ver que la primera fórmula computacional y la segunda fórmula computacional anterior generalizan las fórmulas computacionales para la varianza muestral. Claramente, la covarianza muestral es simétrica.
\(s(\bs{x}, \bs{y}) = s(\bs{y}, \bs{x})\).
La covarianza de la muestra es lineal en el primer argumento con el segundo argumento fijo.
Si\(\bs{x}\),\(\bs{y}\), y\(\bs{z}\) son vectores de datos de variables de población\(x\)\(y\), y\(z\), respectivamente, y si\(c\) es una constante, entonces
- \(s(\bs{x} + \bs{y}, \bs{z}) = s(\bs{x}, \bs{z}) + s(\bs{y}, \bs{z})\)
- \(s(c \bs{x}, \bs{y}) = c s(\bs{x}, \bs{y})\)
Prueba
- Recordemos eso\(m(\bs{x} + \bs{y}) = m(\bs{x}) + m(\bs{y})\). De ahí\ begin {align} s (\ bs {x} +\ bs {y},\ bs {z}) & =\ frac {1} {n - 1}\ sum_ {i=1} ^n [x_i + y_i - m (\ bs {x} +\ bs {y})] [z_i - m (\ bs {z})]\\ & =\ frac {1} {n - 1}\ suma_ {i=1} ^n\ izquierda ([x_i - m (\ bs {x})] + [y_i - m (\ bs {y})]\ derecha) [z_i - m (\ bs {z})]\\ & =\ frac {1} {n - 1}\ sum_ {i=1} ^n [x_i - m (\ bs {x})] [z_i - m (\ bs {z} )] +\ frac {1} {n - 1}\ suma_ {i=1} ^n [y_i - m (\ bs {y})] [z_i - m (\ bs {z})]\\ & = s (\ bs {x},\ bs {z}) + s (\ bs {y},\ bs {z})\ end align {}
- Recordemos eso\(m(c \bs{x}) = c m(\bs{x})\). De ahí\ begin {align} s (c\ bs {x},\ bs {y}) & =\ frac {1} {n - 1}\ sum_ {i=1} ^n [c x_i - m (c\ bs {x})] [y_i - m (\ bs {y})]\\ & =\ frac {1} {n - 1}\ sum_ {i=1} ^n [c x_i - c m (\ bs {x})] [y_i - m (\ bs {y})] = c s (\ bs {x},\ bs {y})\ end {align}
Por simetría, la covarianza muestral también es lineal en el segundo argumento con el primer argumento fijo, y por lo tanto es bilineal. La versión general de la propiedad bilineal se da en el siguiente teorema:
Supongamos que\(\bs{x}_i\) es un vector de datos de una variable de población\(x_i\) para\(i \in \{1, 2, \ldots, k\}\) y que\(\bs{y}_j\) es un vector de datos de una variable de población\(y_j\) para\(j \in \{1, 2, \ldots, l\}\). Supongamos también eso\(a_1, \, a_2, \ldots, \, a_k\) y\(b_1, \, b_2, \ldots, b_l\) son constantes. Entonces\[ s \left( \sum_{i=1}^k a_i \, \bs{x}_i, \sum_{j = 1}^l b_j \, \bs{y}_j \right) = \sum_{i=1}^k \sum_{j=1}^l a_i \, b_j \, s(\bs{x}_i, \bs{y}_j) \]
Un caso especial de la propiedad bilineal proporciona una buena manera de calcular la varianza de muestra de una suma.
\(s^2(\bs{x} + \bs{y}) = s^2(\bs{x}) + 2 s(\bs{x}, \bs{y}) + s^2(\bs{y})\).
Prueba
De los resultados anteriores,\ begin {align} s^2 (\ bs {x} +\ bs {y}) & = s (\ bs {x} +\ bs {y},\ bs {x} +\ bs {y}) = s (\ bs {x},\ bs {x}) + s (\ bs {x},\ bs {y}) + s (\ bs {y},\ bs {x}) + s (\ bs {y},\ bs {y})\\ & = s^2 (\ bs {x}) + 2 s (\ bs {x},\ bs {y}) + s^2 (\ bs {y})\ end {align}
La generalización de este resultado a sumas de tres o más vectores es completamente sencilla: es decir, la varianza muestral de una suma es la suma de todas las covarianzas muestrales por pares. Obsérvese que la varianza muestral de una suma puede ser mayor que, menor o igual a la suma de las varianzas de la muestra, dependiendo del signo y magnitud del término de covarianza pura. En particular, si los vectores no están correlacionados por pares, entonces la varianza de la suma es la suma de las varianzas.
Si\(\bs{c}\) es un conjunto de datos constante entonces\(s(\bs{x}, \bs{c}) = 0\).
Prueba
Esto se desprende directamente de la definición. Si\(c_i = c\) para cada uno\(i\), entonces\(m(\bs{c}) = c\) y por lo tanto\(c_i - m(\bs{c}) = 0\) para cada uno\(i\).
Combinando el resultado en el último ejercicio con la propiedad bilineal, vemos que la covarianza no cambia si se agregan constantes a los conjuntos de datos. Es decir, si\(\bs{c}\) y\(\bs{d}\) son vectores constantes entonces\(s(\bs{x}+ \bs{c}, \bs{y} + \bs{d}) = s(\bs{x}, \bs{y})\).
Propiedades de Correlación
A continuación se dan algunas propiedades simples de correlación. La mayoría de estos se derivan fácilmente de las correspondientes propiedades de covarianza. Primero, recordemos que las puntuaciones estándar de\(x_i\) y\(y_i\) son, respectivamente,\[ u_i = \frac{x_i - m(\bs{x})}{s(\bs{x})}, \quad v_i = \frac{y_i - m(\bs{y})}{s(\bs{y})} \] Las puntuaciones estándar de un conjunto de datos son cantidades adimensionales que tienen media 0 y varianza 1.
La correlación entre\(\bs{x}\) y\(\bs{y}\) es la covarianza de sus puntuaciones estándar\(\bs{u}\) y\(\bs{v}\). Es decir,\(r(\bs{x}, \bs{y}) = s(\bs{u}, \bs{v})\).
Prueba
En notación vectorial, tenga en cuenta que\[ \bs{u} = \frac{1}{s(\bs{x})}[\bs{x} - m(\bs{x})], \quad \bs{v} = \frac{1}{s(\bs{y})}[\bs{y} - m(\bs{y})] \] De ahí el resultado sigue inmediatamente de las propiedades de covarianza:\[ s(\bs{u}, \bs{v}) = \frac{1}{s(\bs{x}) s(\bs{y})} s(\bs{x}, \bs{y}) = r(\bs{x}, \bs{y}) \]
La correlación es simétrica.
\(r(\bs{x}, \bs{y}) = r(\bs{y}, \bs{x})\).
A diferencia de la covarianza, la correlación no se ve afectada al multiplicar uno de los conjuntos de datos por una constante positiva (recordemos que esto siempre se puede considerar como un cambio de escala en la variable subyacente). Por otro lado, la multiplicación de un conjunto de datos por una constante negativa cambia el signo de la correlación.
Si\(c \ne 0\) es una constante entonces
- \(r(c \bs{x}, \bs{y}) = r(\bs{x}, \bs{y})\)si\(c \gt 0\)
- \(r(c \bs{x}, \bs{y}) = -r(\bs{x}, \bs{y})\)si\(c \lt 0\)
Prueba
Por definición y a partir de la propiedad de escalado de la covarianza,\[ r(c \bs{x}, \bs{y}) = \frac{s(c \bs{x}, \bs{y})}{s(c \bs{x}) s(\bs{y})} = \frac{c s(\bs{x}, \bs{y})}{\left|c\right| s(\bs{x}) s(\bs{y})} = \frac{c}{\left|c\right|} r(\bs{x}, \bs{y}) \] y por supuesto,\( c / \left|c\right| = 1 \) si\( c \gt 0 \) y\( c / \left|c\right| = -1 \) si\( c \lt 0 \).
Al igual que la covarianza, la correlación no se ve afectada al agregar constantes a los conjuntos de datos. Agregar una constante a un conjunto de datos a menudo corresponde a un cambio de ubicación.
Si\(\bs{c}\) y\(\bs{d}\) son vectores constantes entonces\(r(\bs{x} + \bs{c}, \bs{y} + \bs{d}) = r(\bs{x}, \bs{y})\).
Prueba
Este resultado se deriva directamente de las propiedades correspondientes de covarianza y desviación estándar:\[ r(\bs{x} + \bs{c}, \bs{y} + \bs{d}) = \frac{s(\bs{x} + \bs{c}, \bs{y} + \bs{d})}{s(\bs{x} + \bs{c}) s(\bs{y} + \bs{d})} = \frac{s(\bs{x}, \bs{y})}{s(\bs{x}) s(\bs{y})} = r(\bs{x}, \bs{y}) \]
El último par de propiedades refuerzan el hecho de que la correlación es una medida estandarizada de asociación que no se ve afectada por el cambio de las unidades de medida. En el primer conjunto de datos Challenger, por ejemplo, las variables de interés son la temperatura al momento del lanzamiento (en grados Fahrenheit) y la erosión de la junta tórica (en milímetros). La correlación entre estas variables es de importancia crítica. Si mediéramos la temperatura en grados Celsius y la erosión de la junta tórica en pulgadas, la correlación entre las dos variables se mantendría sin cambios.
Las propiedades más importantes de correlación surgen del estudio de la línea que mejor se ajusta a los datos, nuestro siguiente tema.
Regresión lineal
Nos interesa encontrar la línea\(y = a + b x\) que mejor se ajuste a los puntos de muestreo\(\left((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\right)\). Se trata de un problema básico e importante en muchas áreas de las matemáticas, no sólo de la estadística. Pensamos en\(x\) ella como la variable predictora y\(y\) como la variable de respuesta. Así, el término mejor significa que queremos encontrar la línea (es decir, encontrar los coeficientes\(a\) y\(b\)) que minimiza el promedio de los errores al cuadrado entre\(y\) los valores reales en nuestros datos y los\(y\) valores predichos:\[ \mse(a, b) = \frac{1}{n - 1} \sum_{i=1}^n [y_i - (a + b \, x_i)]^2 \] Tenga en cuenta que el valor minimizador de\((a, b)\) sería lo mismo si la función fuera simplemente la suma de los errores cuadrados, de si promediamos dividiendo por\(n\) en lugar de\(n - 1\), o si usamos la raíz cuadrada de alguna de estas funciones. Por supuesto que ese valor mínimo real de la función sería diferente si cambiáramos la función, pero nuevamente, no el punto\((a, b)\) donde ocurre el mínimo. Nuestra elección particular de\(\mse\) como la función de error es mejor para fines estadísticos. Encontrar\((a, b)\) que minimizar\(\mse\) es un problema estándar en el cálculo.
La gráfica de\(\mse\) es una apertura paraboloide hacia arriba. La función\(\mse\) se minimiza cuando\ begin {align} b (\ bs {x},\ bs {y}) & =\ frac {s (\ bs {x},\ bs {y})} {s^2 (\ bs {x})}\\ a (\ bs {x},\ bs {y}) & = m (\ bs {y}) - b (\ bs {x},\ bs {y}) m (\ bs {x}) = m (\ bs {y}) -\ frac {s (\ bs {x},\ bs {y})} {s^2 (\ bs {x})} m (\ bs {x})\ end {align}
Prueba
Podemos decir por la forma algebraica de\( \mse \) que la gráfica es un paraboloide que se abre hacia arriba. Para encontrar el punto único que minimiza\( \mse \), tenga en cuenta que\ begin {align}\ frac {\ parcial} {\ parcial a}\ mse (a, b) & =\ frac {1} {n - 1}\ sum 2 [y_i - (a + b x_i)] (-1) =\ frac {2} {n - 1} [-\ sum_ {i=1} ^n y_i + n a + b\ suma_ {i=1} ^n x_i]\\ frac {\ parcial} {\ parcial b}\ mse (a, b) & =\ frac {1} {n - 1}\ suma 2 [y_i - ( a + b x_i)] (-x_i) =\ frac {2} {n - 1} [-\ suma_ {i=1} ^n x_i y_i + a\ suma_ {i=1} ^n x_i + b\ sum_ {i=1} ^n x_i^2]\ end {align} Resolviendo\( \frac{\partial}{\partial a} \mse(a, b) = 0 \), da\( a = m(\bs{y}) - b m(\bs{x}) \). Sustituyendo esto en\(\frac{\partial}{\partial b} \mse(a, b) = 0 \) y resolviendo por\( b \) da\[ b = \frac{n[m(\bs{x} \bs{y}) - m(\bs{x}) m(\bs{y})]}{n[m(\bs{x}^2) - m^2(\bs{x})]} \] Dividiendo el numerador y denominador en la última expresión por\( n - 1 \) y usando la fórmula computacional anterior, vemos eso\( b = s(\bs{x}, \bs{y}) / s^2(\bs{x}) \).
Por supuesto, los valores óptimos de\(a\) y\(b\) son estadísticas, es decir, funciones de los datos. Así, la línea de regresión muestral es\[ y = m(\bs{y}) + \frac{s(\bs{x}, \bs{y})}{s^2(\bs{x})} [x - m(\bs{x})] \]
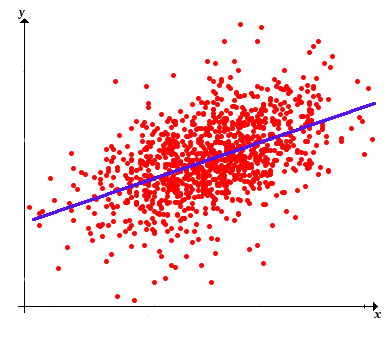
Tenga en cuenta que la línea de regresión pasa por el punto\(\left(m(\bs{x}), m(\bs{y})\right)\), el centro de la muestra de puntos.
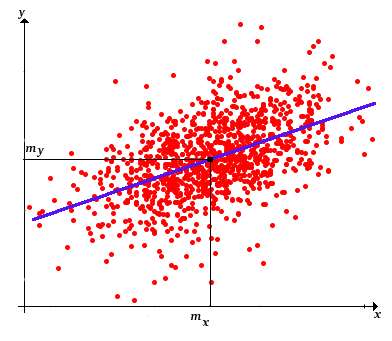
El error cuadrático medio mínimo es\[ \mse\left[a(\bs{x}, \bs{y}), b(\bs{x}, \bs{y})\right] = s(\bs{y})^2 \left[1 - r^2(\bs{x}, \bs{y})\right] \]
Prueba
Esto se deduce de sustituir\( a(\bs{x}, \bs{y}) \)\( b(\bs{x}, \bs{y}) \)\( \mse \) y simplificar.
La correlación muestral y la covarianza satisfacen las siguientes propiedades.
- \(-1 \le r(\bs{x}, \bs{y}) \le 1\)
- \(-s(\bs{x}) s(\bs{y}) \le s(\bs{x}, \bs{y}) \le s(\bs{x}) s(\bs{y})\)
- \(r(\bs{x}, \bs{y}) = -1\)si y sólo si los puntos de muestreo se encuentran en una línea con pendiente negativa.
- \(r(\bs{x}, \bs{y}) = 1\)si y sólo si los puntos de muestreo se encuentran en una línea con pendiente positiva.
Prueba
Tenga en cuenta que\( \mse \ge 0 \) y de ahí a partir del teorema anterior, debemos tener\( r^2(\bs{x}, \bs{y}) \le 1 \). Esto equivale a la parte (a), que a su vez, a partir de la definición de correlación muestral, equivale a la parte (b). Para las partes (c) y (d), tenga en cuenta que\( \mse(a, b) = 0 \) si y sólo si\( y_i = a + b x_i \) para cada una\( i \), y además,\( b(\bs{x}, \bs{y}) \) tiene el mismo signo que\( r(\bs{x}, \bs{y}) \).
Así, ahora vemos de manera más profunda que la covarianza y correlación muestrales miden el grado de linealidad de los puntos de muestra. Recordemos de nuestra discusión de medidas de centro y propagación que la constante\(a\) que minimiza\[ \mse(a) = \frac{1}{n - 1} \sum_{i=1}^n (y_i - a)^2 \] es la media muestral\(m(\bs{y})\), y el valor mínimo del error cuadrático medio es la varianza muestral\(s^2(\bs{y})\). Así, la diferencia entre este valor del error cuadrático medio y el anterior,\(s^2(\bs{y}) r^2(\bs{x}, \bs{y})\) es decir, es la reducción en la variabilidad de\(y\) los datos cuando el término lineal in\(x\) se suma al predictor. La reducción fraccionaria es\(r^2(\bs{x}, \bs{y})\), y de ahí que esta estadística se llame el coeficiente de determinación (muestra). Obsérvese que si los vectores de datos\(\bs{x}\) y no\(\bs{y}\) están correlacionados, entonces no\(x\) tiene valor como predictor de\(y\); la línea de regresión en este caso es la línea horizontal\(y = m(\bs{y})\) y el error cuadrático medio es\(s^2(\bs{y})\).
La elección de las variables predictoras y de respuesta es importante.
La línea de regresión de muestra con variable predictora\(x\) y variable de respuesta no\(y\) es la misma que la línea de regresión de muestra con variable predictora\(y\) y variable de respuesta\(x\), excepto en el caso extremo\(r(\bs{x}, \bs{y}) = \pm 1\) donde todos los puntos de muestra se encuentran en una línea.
Residuales
La diferencia entre el\(y\) valor real de un punto de datos y el valor predicho por la línea de regresión se denomina residual de ese punto de datos. Así, el residual correspondiente a\((x_i, y_i)\) es\( d_i = y_i - \hat{y}_i \) donde\( \hat{y}_i \) está la línea de regresión en\( x_i \):\[ \hat{y}_i = m(\bs{y}) + \frac{s(\bs{x}, \bs{y})}{s(\bs{x})^2} [x_i - m(\bs{x})] \] Tenga en cuenta que el valor predicho\(\hat{y}_i\) y el residual\(d_i\) son estadísticas, es decir, funciones de los datos\((\bs{x}, \bs{y})\), pero estamos suprimiendo esto en el notación para la simplicidad.
Los residuos se suman a 0:\( \sum_{i=1}^n d_i = 0 \).
Prueba
Esto se desprende de la definición, y es una reafirmación del hecho de que la línea de regresión pasa por el centro del conjunto de datos\( \left(m(\bs{x}), m(\bs{y})\right) \).
Diversas parcelas de los residuos pueden ayudar a uno a entender la relación entre los\(y\) datos\(x\) y. Algunos de los más comunes se dan en la siguiente definición:
Parcelas residuales
- Una gráfica de\((i, d_i)\) for\(i \in \{1, 2, \ldots, n\}\), es decir, una gráfica de índices versus residuales.
- Una gráfica de\((x_i, d_i)\) for\(i \in \{1, 2, \ldots, n\}\), es decir, una gráfica de\(x\) valores versus residuales.
- Una gráfica de\((d_i, y_i)\) for\(i \in \{1, 2, \ldots, n\}\), es decir, una gráfica de residuos versus\(y\) valores reales.
- Una gráfica de\((d_i, \hat{y}_i)\) for\(i \in \{1, 2, \ldots, n\}\), es decir, una gráfica de residuos versus\(y\) valores predichos.
- Un histograma de los residuos\((d_1, d_2, \ldots, d_n)\).
Sumas de Cuadrados
Para nuestra próxima discusión, reinterpretaremos la fórmula de error cuadrático medio mínimo anterior. Aquí están las nuevas definiciones:
Sumas de cuadrados
- \(\sst(\bs{y}) = \sum_{i=1}^n [y_i - m(\bs{y})]^2 \)es la suma total de cuadrados.
- \(\ssr(\bs{x}, \bs{y}) = \sum_{i=1}^n [\hat{y}_i - m(\bs{y})]^2 \)es la suma de regresión de cuadrados
- \(\sse(\bs{x}, \bs{y}) = \sum_{i=1}^n (y_i - \hat{y}_i)^2\)es la suma del error de los cuadrados.
Obsérvese que\(\sst(\bs{y})\) es simplemente\(n - 1\) multiplicado por la varianza\(s^2(\bs{y})\) y es el total de las sumas de los cuadrados de las desviaciones de\(y\) los valores de la media de los\(y\) valores. Del mismo modo,\(\sse(\bs{x}, \bs{y})\) es simplemente\(n - 1\) multiplicado por el mínimo error cuadrático medio dado anteriormente. Por supuesto,\(\sst(\bs{y})\) tiene\(n - 1\) grados de libertad, mientras que\(\sse(\bs{x}, \bs{y})\) tiene\(n - 2\) grados de libertad y\(\ssr(\bs{x}, \bs{y})\) un solo grado de libertad. La suma total de cuadrados es la suma de la suma de regresión de cuadrados y la suma de errores de cuadrados:
Las sumas de cuadrados se relacionan de la siguiente manera:
- \(\ssr(\bs{x}, \bs{y}) = r^2(\bs{x}, \bs{y}) \sst(\bs{y})\)
- \(\sst(\bs{y}) = \ssr(\bs{x}, \bs{y}) + \sse(\bs{x}, \bs{y})\)
Prueba
Por definición de\(\sst\) y\(r\), vemos eso\(r^2(\bs{x}, \bs{y}) \sst(\bs{y}) = s^2(\bs{x}, \bs{y}) \big/ s^2(\bs{x})\). Pero a partir de la ecuación de regresión,\[ [\hat{y}_i - m(\bs{y})]^2 = \frac{s^2(\bs{x}, \bs{y})}{s^4(\bs{x})} [x_i - m(\bs{x})]^2\] Sumando sobre\(i\) da\[ \ssr(\bs{x}, \bs{y}) = \sum_{i=1}^n [\hat{y}_i - m(\bs{y})]^2 = \frac{s^2(\bs{x}, \bs{y})}{s^2(\bs{x})} \] De ahí\(\ssr(\bs{x}, \bs{y}) = r^2(\bs{x}, \bs{y}) \sst(\bs{y})\). Por último, multiplicando el resultado anterior por\(n - 1\) da\(\sse(\bs{x}, \bs{y}) = \sst(\bs{y}) - r^2(\bs{x}, \bs{y}) \sst(\bs{y}) = \sst(\bs{y}) - \ssr(\bs{x}, \bs{y})\).
Obsérvese que\(r^2(\bs{x}, \bs{y}) = \ssr(\bs{x}, \bs{y}) \big/ \sst(\bs{y})\), así una vez más,\(r^2(\bs{x}, \bs{y})\) es el coeficiente de determinación, la proporción de la variabilidad en los\(y\) datos explicados por los\(x\) datos. Podemos promediar dividiendo\(\sse\) por sus grados de libertad y luego tomar la raíz cuadrada para obtener un error estándar:
El error estándar de estimación es\[ \se(\bs{x}, \bs{y}) = \sqrt{\frac{\sse(\bs{x}, \bs{y})}{n - 2}} \]
Esto realmente es un error estándar en el mismo sentido que una desviación estándar. Es un promedio de las clases de errores, pero en el sentido raíz cuadrático medio.
Por último, es importante señalar que la regresión lineal es una idea mucho más poderosa de lo que podría aparecer primero, y de hecho el término lineal puede ser un poco engañoso. Al aplicar diversas transformaciones a\(y\)\(x\) o ambas, podemos ajustar una variedad de curvas de dos parámetros a los datos dados\(\left((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\right)\). Algunas de las transformaciones más comunes se exploran en los ejercicios siguientes.
Teoría de Probabilidad
Continuamos nuestra discusión sobre la covarianza muestral, correlación y regresión pero ahora desde el punto de vista más interesante que las variables son aleatorias. Específicamente, supongamos que tenemos un experimento aleatorio básico, y que\(X\) y que\(Y\) son variables aleatorias de valor real para el experimento. Equivalentemente,\((X, Y)\) es un vector aleatorio tomando valores en\(\R^2\). Dejar\(\mu = \E(X)\) y\(\nu = \E(Y)\) denotar las medias de distribución,\(\sigma^2 = \var(X)\) y\(\tau^2 = \var(Y)\) las varianzas de distribución, y dejar\(\delta = \cov(X, Y)\) denotar la covarianza de distribución, para que la correlación de distribución sea\[ \rho = \cor(X, Y) = \frac{\cov(X, Y)}{\sd(X) \, \sd(Y)} = \frac{\delta}{\sigma \, \tau} \] También necesitaremos algunos momentos de orden superior. Vamos\(\sigma_4 = \E\left[(X - \mu)^4\right]\),\(\tau_4 = \E\left[(Y - \nu)^4\right]\), y\(\delta_2 = \E\left[(X - \mu)^2 (Y - \nu)^2\right]\). Naturalmente, asumimos que todos estos momentos son finitos.
Ahora supongamos que ejecutamos los\(n\) tiempos básicos del experimento. Esto crea un experimento compuesto con una secuencia de vectores aleatorios independientes\(\left((X_1, Y_1), (X_2, Y_2), \ldots, (X_n, Y_n)\right)\) cada uno con la misma distribución que\((X, Y)\). En términos estadísticos, se trata de una muestra aleatoria de tamaño\(n\) a partir de la distribución de\((X, Y)\). Las estadísticas discutidas en la sección anterior están bien definidas pero ahora todas son variables aleatorias. Utilizamos la notación establecida previamente, excepto que usamos nuestra convención habitual de denotar variables aleatorias con mayúsculas. Por supuesto, las propiedades deterministas y las relaciones establecidas anteriormente aún se mantienen. Tenga en cuenta que\(\bs{X} = (X_1, X_2, \ldots, X_n)\) es una muestra aleatoria de tamaño\(n\) a partir de la distribución de\(X\) y\(\bs{Y} = (Y_1, Y_2, \ldots, Y_n)\) es una muestra aleatoria de tamaño\(n\) a partir de la distribución de\(Y\). El propósito principal de esta subsección es estudiar la relación entre diversas estadísticas de\(\bs{X}\) y\(\bs{Y}\), y estudiar estadísticas que son estimadores naturales de la covarianza y correlación de la distribución.
Las medias de la muestra
Recordemos que las medias de muestra son\[ M(\bs{X}) = \frac{1}{n} \sum_{i=1}^n X_i, \quad M(\bs{Y}) = \frac{1}{n} \sum_{i=1}^n Y_i \] De las secciones sobre la ley de los grandes números y el teorema del límite central, sabemos mucho sobre las distribuciones de\(M(\bs{X})\) e\(M(\bs{Y})\) individualmente. Pero necesitamos saber más sobre la distribución conjunta.
La covarianza y correlación entre\(M(\bs{X})\) y\(M(\bs{Y})\) son
- \(\cov[M(\bs{X}), M(\bs{Y})] = \delta / n\)
- \(\cor[(M(\bs{X}), M(\bs{Y})] = \rho\)
Prueba
La parte (a) se desprende de la bilinaridad del operador de covarianza:\[ \cov\left(\frac{1}{n} \sum_{i=1}^n X_i, \frac{1}{n} \sum_{j=1}^n Y_j\right) = \frac{1}{n^2}\sum_{i=1}^n \sum_{j=1}^n \cov(X_i, Y_j)\] Por independencia, los términos en la última suma son 0 si\(i \ne j\). Para\(i = j\) los términos son\(\cov(X, Y) = \delta\). Hay\(n\) tales términos así\(\cov[M(\bs{X}), M(\bs{Y})] = \delta / n\). Para la parte b), recordemos que\(\var[M(\bs{X})] = \sigma^2 / n\) y\(\var[M(\bs{Y})] = \tau^2 / n\). De ahí\[ \cor[M(\bs{X}), M(\bs{Y})] = \frac{\delta / n}{(\sigma / \sqrt{n}) (\tau / \sqrt{n})} = \frac{\delta}{\sigma \tau} = \rho\]
Obsérvese que la correlación entre las medias de la muestra es la misma que la correlación de la distribución de muestreo subyacente. En particular, la correlación no depende del tamaño de la muestra\(n\).
Las varianzas de la muestra
Recordemos que las versiones especiales de las varianzas muestrales, en el improbable caso de que se conozcan las medias de distribución, son\[ W^2(\bs{X}) = \frac{1}{n} \sum_{i=1}^n (X_i - \mu)^2, \quad W^2(\bs{Y}) = \frac{1}{n} \sum_{i=1}^n (Y_i - \nu)^2 \] Una vez más, hemos estudiado estas estadísticas de manera individual, por lo que nuestro énfasis ahora está en la distribución conjunta.
La covarianza y correlación entre\(W^2(\bs{X})\) y\(W^2(\bs{Y})\) son
- \(\cov[W^2(\bs{X}), W^2(\bs{Y})] = (\delta_2 - \sigma^2 \tau^2) \big/ n\)
- \(\cor[W^2(\bs{X}), W^2(\bs{Y})] = (\delta_2 - \sigma^2 \tau^2) \big/ \sqrt{(\sigma_4 - \sigma^4)(\tau_4 - \tau^4)}\)
Prueba
Para la parte (a), utilizamos la bilinaridad del operador de covarianza para obtener\[ \cov[W^2(\bs{X}), W^2(\bs{Y})] = \cov\left(\frac{1}{n} \sum_{i=1}^n (X_i - \mu)^2, \frac{1}{n} \sum_{j=1}^n (Y_j - \nu)^2\right) = \frac{1}{n^2} \sum_{i=1}^n \sum_{j=1}^n \cov[(X_i - \mu)^2, (Y_j - \nu)^2] \] Por independencia, los términos en la última suma son 0 cuando\(i \ne j\). Cuando\(i = j\) los términos son\[ \cov[(X - \mu)^2 (Y - \nu)^2] = \E[(X - \mu)^2 (Y - \nu)^2] - \E[(X - \mu)^2] \E[(Y - \nu)^2] = \delta_2 - \sigma^2 \tau^2 \] Hay\(n\) tales términos, entonces\(\cov[W^2(\bs{X}), W^2(\bs{Y})] = (\delta_2 - \sigma^2 \tau^2) \big/ n\). La parte (b) se desprende de la parte (a) y las varianzas de\(W^2(\bs{X})\) y\(W^2(\bs{Y})\) de la sección de Varianza de la Muestra.
Tenga en cuenta que la correlación no depende del tamaño de la muestra\(n\). A continuación, recordemos que las versiones estándar de las varianzas de la muestra son\[ S^2(\bs{X}) = \frac{1}{n - 1} \sum_{i=1}^n [X_i - M(\bs{X})]^2, \quad S^2(\bs{Y}) = \frac{1}{n - 1} \sum_{i=1}^n [Y_i - M(\bs{Y})]^2 \]
La covarianza y correlación de las varianzas muestrales son
- \(\cov[S^2(\bs{X}), S^2(\bs{Y})] = (\delta_2 - \sigma^2 \tau^2) \big/ n + 2 \delta^2 / [n (n - 1)]\)
- \(\cor[S^2(\bs{X}), S^2(\bs{Y})] = [(n - 1)(\delta_2 - \sigma^2 \tau^2) + 2 \delta^2] \big/ \sqrt{[(n - 1) \sigma_4 - (n - 3) \sigma^4][(n - 1) \tau_4 - (n - 3) \tau^4]}\)
Prueba
Recordemos que\[ S^2(\bs{X}) = \frac{1}{2 n (n - 1)} \sum_{i=1}^n \sum_{j=1}^n (X_i - X_j)^2, \quad S^2(\bs{Y}) = \frac{1}{2 n (n - 1)} \sum_{k=1}^n \sum_{l=1}^n (Y_k - Y_l)^2 \] Por lo tanto usando la bilinaridad del operador de covarianza\[ \cov[S^2(\bs{X}), S^2(\bs{Y})] = \frac{1}{4 n^2 (n - 1)^2} \sum_{i=1}^n \sum_{j=1}^n \sum_{k=1}^n \sum_{l=1}^n \cov[(X_i - X_j)^2, (Y_k - Y_l)^2] \] tenemos Calculamos las covarianzas en esta suma considerando casos disjuntos:
- \(\cov[(X_i - X_j)^2, (Y_k - Y_l)^2] = 0\)si\(i = j\) o si\(k = l\), y existen\(2 n^3 - n^2\) tales términos.
- \(\cov[(X_i - X_j)^2, (Y_k - Y_l)^2] = 0\)por independencia si\(i, j, k, l\) son distintos, y existen\(n (n - 1)(n - 2)(n - 3)\) tales términos.
- \(\cov[(X_i - X_j)^2, (Y_k - Y_l)^2] = 2 \delta_2 - 2 \sigma^2 \tau^2 + 4 \delta^2\)si\(i \ne j\) y\(\{k, l\} = \{i, j\}\), y existen\(2 n (n - 1)\) tales términos.
- \(\cov[(X_i - X_j)^2, (Y_k - Y_l)^2] = \delta_2 - \sigma^2 \tau^2\)si\(i \ne j\),\(k \ne l\), y\(\#(\{i, j\} \cap \{k, l\}) = 1\), y existen\(4 n (n - 1)(n - 2)\) tales términos.
Sustituir y simplificar da el resultado en (a). Para (b), utilizamos la definición de correlación y las fórmulas para\(\var[S^2(\bs{X})]\) y\(\var[S^2(\bs{Y})]\) desde la sección sobre la varianza de la muestra.
Asintóticamente, la correlación entre las varianzas muestrales es la misma que la correlación entre las varianzas de muestra especiales dadas anteriormente:\[ \cor\left[S^2(\bs{X}), S^2(\bs{Y})\right] \to \frac{\delta_2 - \sigma^2 \tau^2}{\sqrt{(\sigma_4 - \sigma^4)(\tau_4 - \tau^4)}} \text{ as } n \to \infty \]
Covarianza muestral
Supongamos primero que los medios de distribución\(\mu\) y\(\nu\) son conocidos. Como se señaló anteriormente, esto es casi siempre una suposición poco realista, pero sigue siendo un buen lugar para comenzar porque el análisis es muy sencillo y los resultados que obtengamos serán útiles a continuación. Un estimador natural de la covarianza de distsribución\(\delta = \cov(X, Y)\) en este caso es la covarianza de muestra especial\[ W(\bs{X}, \bs{Y}) = \frac{1}{n} \sum_{i=1}^n (X_i - \mu)(Y_i - \nu) \] Tenga en cuenta que la covarianza de muestra especial generaliza la varianza especial de la muestra:\(W(\bs{X}, \bs{X}) = W^2(\bs{X})\).
\(W(\bs{X}, \bs{Y})\)es la media muestral para una muestra aleatoria de tamaño\(n\) a partir de la distribución de\((X - \mu)(Y - \nu)\) y satisface las siguientes propiedades:
- \(\E[W(\bs{X}, \bs{Y})] = \delta\)
- \(\var[W(\bs{X}, \bs{Y})] = \frac{1}{n}(\delta_2 - \delta^2)\)
- \(W(\bs{X}, \bs{Y}) \to \delta\)como\(n \to \infty\) con probabilidad 1
Prueba
Estos resultados siguen directamente de la sección sobre la Ley de Grandes Números. Para la parte b), tenga en cuenta que\[ \var[(X - \mu)(Y - \nu)] = \E[(X - \mu)^2 (Y - \nu)^2] - \left(\E[(X - \mu)(Y - \nu)]\right)^2 = \delta_2 - \delta^2 \]
Como estimador de\(\delta\), parte (a) significa que\(W(\bs{X}, \bs{Y})\) es imparcial y parte (b) significa que\(W(\bs{X}, \bs{Y})\) es consistente.
Consideremos ahora la suposición más realista de que los medios de distribución\(\mu\) y\(\nu\) son desconocidos. Un enfoque natural en este caso es promediar\([(X_i - M(\bs{X})][Y_i - M(\bs{Y})]\) sobre\(i \in \{1, 2, \ldots, n\}\). Pero en lugar de dividirnos por\(n\) en nuestro promedio, debemos dividir por cualquier constante que dé un estimador imparcial de\(\delta\). Como se muestra en el siguiente teorema, esta constante resulta ser\(n - 1\), lo que lleva a la covarianza muestral estándar:\[ S(\bs{X}, \bs{Y}) = \frac{1}{n - 1} \sum_{i=1}^n [X_i - M(\bs{X})][Y_i - M(\bs{Y})] \]
\(\E[S(\bs{X}, \bs{Y})] = \delta\).
Prueba
Ampliando como arriba tenemos,\[ \sum_{i=1}^n[X_i - M(\bs{X})][Y_i - M(\bs{Y})] = \sum_{i=1}^n X_i Y_i - n M(\bs{X})M(\bs{Y}) \] Pero\(\E(X_i Y_i) = \cov(X_i, Y_i) + \E(X_i) \E(Y_i) = \delta + \mu \nu\). De igual manera, a partir de la covarianza de las medias muestrales y la propiedad imparcial,\(\E[M(\bs{X}) M(\bs{Y})] = \cov[M(\bs{X}), M(\bs{Y})] + \E[M(\bs{X})] \E[M(\bs{Y})] = \delta / n + \mu \nu\). Así que tomar los valores esperados en la ecuación mostrada arriba da\[ \E\left(\sum_{i=1}^n [X_i - M(\bs{X})][Y_i - M(\bs{Y})]\right) = n ( \delta + \mu \nu) - n (\delta / n + \mu \nu) = (n - 1) \delta \]
\(S(\bs{X}, \bs{Y}) \to \delta\)como\(n \to \infty\) con probabilidad 1.
Prueba
Una vez más, tenemos\[ S(\bs{X}, \bs{Y}) = \frac{n}{n - 1} [M(\bs{X} \bs{Y}) - M(\bs{X}) M(\bs{Y})] \] donde\(M(\bs{X} \bs{Y})\) denota la media muestral para la muestra de los productos\((X_1 Y_1, X_2 Y_2, \ldots, X_n Y_n)\). Por la fuerte ley de los números grandes,\(M(\bs{X}) \to \mu\) como\(n \to \infty\),\(M(\bs{Y}) \to \nu\) como\(n \to \infty\), y\(M(\bs{X} \bs{Y}) \to \E(X Y) = \delta + \mu \nu\) como\(n \to \infty\), cada uno con probabilidad 1. Entonces el resultado sigue dejando\(n \to \infty\) entrar la ecuación mostrada.
De courese, la correlación muestral es\[ R(\bs{X}, \bs{Y}) = \frac{S(\bs{X}, \bs{Y})}{S(\bs{X}) \, S(\bs{Y})} \] Dado que la correlación muestral\(R(\bs{X}, \bs{Y})\) es una función no lineal de la covarianza muestral y las desviaciones estándar de la muestra, no será en general un estimador imparcial de la correlación de distribución\(\rho\). En la mayoría de los casos, sería difícil incluso calcular la media y varianza de\(R(\bs{X}, \bs{Y})\). Sin embargo, podemos mostrar convergencia de la correlación muestral con la correlación de distribución.
\(R(\bs{X}, \bs{Y}) \to \rho\)como\(n \to \infty\) con probabilidad 1.
Prueba
Esto se desprende inmediatamente de la fuerte ley de grandes números y resultados previos. Del resultado anterior\(S(\bs{X}, \bs{Y}) \to \delta\) como\(n \to \infty\), y de la sección sobre la varianza muestral,\(S(\bs{X}) \to \sigma\) como\(n \to \infty\) y\(S(\bs{Y}) \to \tau\) como\(n \to \infty\), cada uno con probabilidad 1. De ahí\(R(\bs{X}, \bs{Y}) \to \delta / \sigma \tau = \rho\) como\(n \to \infty\) con probabilidad 1.
Nuestro siguiente teorema da una formuala para la varianza de la covarianza muestral, ¡no debe confundirse con la covarianza de las varianzas muestrales dadas anteriormente!
La varianza de la covarianza muestral es\[ \var[S(\bs{X}, \bs{Y})] = \frac{1}{n} \left( \delta_2 + \frac{1}{n - 1} \sigma^2 \, \tau^2 - \frac{n - 2}{n - 1} \delta^2 \right) \]
Prueba
Recordemos primero que\[ S(\bs{X}, \bs{Y}) = \frac{1}{2 \, n \, (n - 1)} \sum_{i=1}^n \sum_{j=1}^n (X_i - X_j)(Y_i - Y_j) \] De ahí que usando la bilinaridad del operador de covarianza\[ \var[S(\bs{X}), \bs{Y})] = \frac{1}{4 n^2 (n - 1)^2} \sum_{i=1}^n \sum_{j=1}^n \sum_{k=1}^n \sum_{l=1}^n \cov[(X_i - X_j)(Y_i - Y_j), (X_k - X_l)(Y_k - Y_l)] \] tenemos Calculamos las covarianzas en esta suma considerando casos disjuntos:
- \(\cov[(X_i - X_j)(Y_i - Y_j), (X_k - X_l)(Y_k - Y_l)] = 0\)si\(i = j\) o si\(k = l\), y existen\(2 n^3 - n^2\) tales términos.
- \(\cov[(X_i - X_j)(Y_i - Y_j), (X_k - X_l)(Y_k - Y_l)] = 0\)si\(i, j, k, l\) son distintos, y existen\(n (n - 1)(n - 2)(n - 3)\) tales términos.
- \(\cov[(X_i - X_j)(Y_i - Y_j), (X_k - X_l)(Y_k - Y_l)] = 2 \, \delta_2 + 2 \sigma^2 \tau^2\)si\(i \ne j\) y\(\{k, l\} = \{i, j\}\), y existen\(2 n (n - 1)\) tales términos.
- \(\cov[(X_i - X_j)(Y_i - Y_j), (X_k - X_l)(Y_k - Y_l)] = \delta_2 - \delta^2\)si\(i \ne j\),\(k \ne l\), y\(\#(\{i, j\} \cap \{k, l\}) = 1\), y existen\(4 n (n - 1)(n - 2)\) tales términos.
Sustituir y simplificar da el resultado
No es sorprendente que la varianza de la covarianza de la muestra estándar (donde no conocemos las medias de distribución) sea mayor que la varianza de la covarianza de la muestra especial (donde sí conocemos las medias de distribución).
\(\var[S(\bs{X}, \bs{Y})] \gt \var[W(\bs{X}, \bs{Y})]\).
Prueba
De los resultados anteriores, y algunos álgebra simple,\[ \var[S(\bs{X}, \bs{Y})] - \var[W(\bs{X}, \bs{Y})] = \frac{1}{n (n - 1)}(\delta^2 + \sigma^2 \tau^2) \gt 0 \] Pero tenga en cuenta que la diferencia va a 0 como\(n \to \infty\).
\(\var[S(\bs{X}, \bs{Y})] \to 0\)como\(n \to \infty\). Así, la covarianza muestral es un estimador consistente de la covarianza de distribución.
Regresión
En nuestra primera discusión anterior, estudiamos la regresión desde un punto de vista determinista y descriptivo. Los resultados obtenidos se aplicaron únicamente a la muestra. Estadísticamente surgen preguntas más interesantes y profundas cuando los datos provienen de un experimento aleatorio, e intentamos extraer inferencias sobre la distribución subyacente a partir de la regresión muestral. Hay dos modelos que comúnmente surgen. Una es donde la variable de respuesta es aleatoria, pero la variable predictora es determinista. El otro es el modelo que consideramos aquí, donde la variable predictora y la variable de respuesta son ambas aleatorias, de manera que los datos forman una muestra aleatoria a partir de una distribución bivariada.
Así, supongamos nuevamente que tenemos un vector aleatorio básico\((X, Y)\) para un experimento. Recordemos que en la sección sobre correlación (distribución) y regresión, mostramos que el mejor predictor lineal de\(Y\) dado\(X\), en el sentido de minimizar el error cuadrático medio, es la variable aleatoria de\[ L(Y \mid X) = \E(Y) + \frac{\cov(X, Y)}{\var(X)}[X - \E(X)] = \nu + \frac{\delta}{\sigma^2}(X - \mu) \] manera que la línea de regresión de distribución viene dada por\[ y = L(Y \mid X = x) = \nu + \frac{\delta}{\sigma^2}(x - \mu) \] Además, el valor (mínimo) del error cuadrático medio es\(\E\{[Y - L(Y \mid X)]\} = \var(Y)[1 - \cor^2(X, Y)] = r^2 (1 - \rho^2)\).
.png)
Por supuesto, en aplicaciones reales, es poco probable que conozcamos los parámetros de distribución\(\mu\),\(\nu\),\(\sigma^2\), y\(\delta\). Si queremos estimar la línea de regresión de distribución, un enfoque natural sería considerar una muestra aleatoria a\(\left((X_1, Y_1), (X_2, Y_2), \ldots, (X_n, Y_n)\right)\) partir de la distribución de\((X, Y)\) y calcular la línea de regresión de la muestra. Por supuesto, los resultados son exactamente los mismos que en la discusión anterior, salvo que todas las cantidades relevantes son variables aleatorias. La línea de regresión muestral es
\[ y = M(\bs{Y}) + \frac{S(\bs{X}, \bs{Y})}{S^2(\bs{X})}[x - M(\bs{X})] \]
El error cuadrático medio es\(S^2(\bs{Y})[1 - R^2(\bs{X}, \bs{Y})]\) y el coeficiente de determinación es\(R^2(\bs{X}, \bs{Y})\).
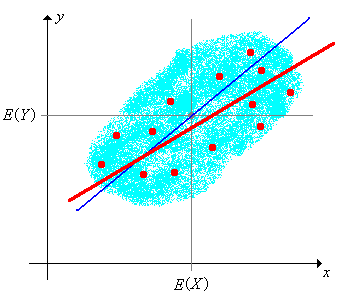
El hecho de que la línea de regresión muestral y el error cuadrático medio sean completamente análogos a la línea de regresión de distribución y el error cuadrático medio es matemáticamente elegante y tranquilizador. Nuevamente, los coeficientes de la línea de regresión muestral pueden verse como estimadores de los respectivos coeficientes en la línea de regresión de distribución.
Los coeficientes de la línea de regresión muestral convergen a los coeficientes de la línea de regresión de distribución con probabilidad 1.
- \(\frac{S(\bs{X}, \bs{Y})}{S^2(\bs{X})} \to \frac{\delta}{\sigma^2}\)como\(n \to \infty\)
- \(M(\bs{Y}) - \frac{S(\bs{X}, \bs{Y})}{S^2(\bs{X})} M(\bs{X}) \to \nu - \frac{\delta}{\sigma^2} \mu\)como\(n \to \infty\)
Prueba
Esto se desprende de la fuerte ley de grandes números y resultados anteriores. con probabilidad 1,\(S(\bs{X}, \bs{Y}) \to \delta\) como\(n \to \infty\),\(S^2(\bs{X}) \to \sigma^2\) como\(n \to \infty\),\(M(\bs{X}) \to \mu\) como\(n \to \infty\), y\(M(\bs{Y}) \to \nu\) como\(n \to \infty\).
Por supuesto, si la relación lineal entre\(X\) y no\(Y\) es fuerte, medida por la correlación muestral, entonces la transformación aplicada a una o ambas variables puede ayudar. Nuevamente, se exploran algunas transformaciones típicas en los ejercicios a continuación.
Ejercicios
Propiedades Básicas
Supongamos que\( x \) y\( y \) son variables poblacionales,\( \bs{x} \) y y\( \bs{y} \) muestras de tamaño\( n \) de\( x \) y\( y \) respectivamente. Supongamos también que\( m(\bs{x}) = 3 \)\( m(\bs{y}) = -1 \),\( s^2(\bs{x} ) = 4\),\( s^2(\bs{y}) = 9 \),, y\( s(\bs{x}, \bs{y}) = 5 \). Encuentra cada uno de los siguientes:
- \(r(\bs{x}, \bs{y})\)
- \( m(2 \bs{x} + 3 \bs{y}) \)
- \( s^2(2 \bs{x} + 3 \bs{y}) \)
- \( s(2 \bs{x} + 3 \bs{y} - 1, 4 \bs{x} + 2 \bs{y} - 3)\)
Supongamos que\(x\) es la temperatura (en grados Fahrenheit) y\(y\) la resistencia (en ohmios) para cierto tipo de componente electrónico después de 10 horas de funcionamiento. Para una muestra de 30 componentes,\(m(\bs{x}) = 113\),\(s(\bs{x}) = 18\),\(m(\bs{y}) = 100\),\(s(\bs{y}) = 10\),\(r(\bs{x}, \bs{y}) = 0.6\).
- Clasificar\(x\) y\(y\) por tipo y nivel de medición.
- Encuentra la covarianza muestral.
- Encuentra la ecuación de la línea de regresión.
Supongamos ahora que la temperatura se convierte a grados Celsius (la transformación es\(\frac{5}{9}(x - 32)\)).
- Encuentra las medias de la muestra.
- Encuentra las desviaciones estándar de la muestra.
- Encuentra la covarianza y correlación de la muestra.
- Encuentra la ecuación de la línea de regresión.
Responder
- continuo, intervalo
- \(m = 45°\),\(s = 10°\)
Supongamos que\(x\) es\(y\) el largo y el ancho (en pulgadas) de una hoja en cierto tipo de planta. Para una muestra de 50 hojas\(m(\bs{x}) = 10\),\(s(\bs{x}) = 2\),\(m(\bs{y}) = 4\),\(s(\bs{y}) = 1\), y\(r(\bs{x}, \bs{y}) = 0.8\).
- Clasificar\(x\) y\(y\) por tipo y nivel de medición.
- Encuentra la covarianza muestral.
- Encuentra la ecuación de la línea de regresión con\(x\) como variable predictora y\(y\) como variable de respuesta.
Supongamos ahora eso\(x\) y\(y\) se convierten a pulgadas (0.3937 pulgadas por centímetro).
- Encuentra las medias de la muestra.
- Encuentra las desviaciones estándar de la muestra.
- Encuentra la covarianza y correlación de la muestra.
- Encuentra la ecuación de la línea de regresión.
Contestar
- continuo, relación
- \(m = 25.4\),\(s = 5.08\)
Ejercicios de Scatterplot
Haga clic en la gráfica de dispersión interactiva, en varios lugares, y observe cómo cambian las medias, las desviaciones estándar, la correlación y la línea de regresión.
Haga clic en la gráfica de dispersión interactiva para definir 20 puntos e intentar acercarse lo más posible a cada una de las siguientes correlaciones de muestra:
- \(0\)
- \(0.5\)
- \(-0.5\)
- \(0.7\)
- \(-0.7\)
- \(0.9\)
- \(-0.9\).
Haga clic en la gráfica de dispersión interactiva para definir 20 puntos. Intentar generar un diagrama de dispersión en el que la línea de regresión tenga
- pendiente 1, intercepción 1
- pendiente 3, intercepción 0
- pendiente\(-2\), intercepción 1
Ejercicios de simulación
Ejecutar el experimento uniforme bivariado 2000 veces en cada uno de los siguientes casos. Comparar las medias de la muestra con las medias de distribución, las desviaciones estándar de la muestra con las desviaciones estándar de distribución, la correlación de la muestra con la correlación de distribución y la línea de regresión de la muestra con la línea de regresión de la distribución.
- La distribución uniforme en la plaza
- La distribución uniforme en el triángulo.
- La distribución uniforme en el círculo.
Ejecutar el experimento normal bivariado 2000 veces para diversos valores de las desviaciones estándar de distribución y la correlación de distribución. Comparar las medias de la muestra con las medias de distribución, las desviaciones estándar de la muestra con las desviaciones estándar de distribución, la correlación de la muestra con la correlación de distribución y la línea de regresión de la muestra con la línea de regresión de la distribución.
Transformaciones
Considera la función\(y = a + b x^2\).
- Esboce la gráfica para algunos valores representativos de\(a\) y\(b\).
- Tenga en cuenta que\(y\) es una función lineal de\(x^2\), con intercepción\(a\) y pendiente\(b\).
- De ahí que para ajustar esta curva a los datos de la muestra, simplemente aplique el procedimiento de regresión estándar a los datos de las variables\(x^2\) y\(y\).
Considera la función\(y = \frac{1}{a + b x}\).
- Esboce la gráfica para algunos valores representativos de\(a\) y\(b\).
- Tenga en cuenta que\(\frac{1}{y}\) es una función lineal de\(x\), con intercepción\(a\) y pendiente\(b\).
- Por lo tanto, para ajustar esta curva a nuestros datos de muestra, simplemente aplicar el procedimiento de regresión estándar a los datos de las variables\(x\) y\(\frac{1}{y}\).
Considera la función\(y = \frac{x}{a + b x}\).
- Esboce la gráfica para algunos valores representativos de\(a\) y\(b\).
- Tenga en cuenta que\(\frac{1}{y}\) es una función lineal de\(\frac{1}{x}\), con intercepción\(b\) y pendiente\(a\).
- De ahí que para ajustar esta curva a los datos de la muestra, simplemente aplique el procedimiento de regresión estándar a los datos de las variables\(\frac{1}{x}\) y\(\frac{1}{y}\).
- Observe nuevamente que los nombres de la intersección y pendiente se invierten a partir de las fórmulas estándar.
Considera la función\(y = a e^{b x}\).
- Esboce la gráfica para algunos valores representativos de\(a\) y\(b\).
- Tenga en cuenta que\(\ln(y)\) es una función lineal de\(x\), con intercepción\(\ln(a)\) y pendiente\(b\).
- De ahí que para ajustar esta curva a los datos de la muestra, simplemente aplique el procedimiento de regresión estándar a los datos de las variables\(x\) y\(\ln(y)\).
- Después de resolver para la interceptación\(\ln(a)\), recuperar la estadística\(a = e^{\ln(a)}\).
Considera la función\(y = a x^b\).
- Esboce la gráfica para algunos valores representativos de\(a\) y\(b\).
- Tenga en cuenta que\(\ln(y)\) es una función lineal de\(\ln(x)\), con intercepción\(\ln(a)\) y pendiente\(b\).
- De ahí que para ajustar esta curva a los datos de la muestra, simplemente aplique el procedimiento de regresión estándar a los datos de las variables\(\ln(x)\) y\(\ln(y)\).
- Después de resolver para la interceptación\(\ln(a)\), recuperar la estadística\(a = e^{\ln(a)}\).
Ejercicios Computacionales
Todos los paquetes de software estadístico realizarán análisis de regresión. Además de la línea de regresión, la mayoría de los paquetes generalmente reportarán el coeficiente de determinación\(r^2(\bs{x}, \bs{y})\), las sumas de cuadrados\(\sst(\bs{y})\)\(\ssr(\bs{x}, \bs{y})\),\(\sse(\bs{x}, \bs{y})\), y el error estándar de estimación\(\se(\bs{x}, \bs{y})\). La mayoría de los paquetes también dibujarán la gráfica de dispersión, con la línea de regresión superpuesta, y dibujarán las diversas gráficas de residuos discutidas anteriormente. Muchos paquetes también proporcionan formas fáciles de transformar los datos. Por lo tanto, hay muy pocas razones para realizar los cálculos a mano, excepto con un pequeño conjunto de datos para dominar las definiciones y fórmulas. En el siguiente problema, haga los cómputos y dibuje las gráficas con ayudas tecnológicas mínimas.
Supongamos que\(x\) es el número de cursos de matemáticas completados y\(y\) el número de cursos de ciencias cursados para un estudiante en Enormous State University (ESU). Una muestra de 10 estudiantes de ESU da los siguientes datos:\(\left((1, 1), (3, 3), (6, 4), (2, 1), (8, 5), (2, 2), (4, 3), (6, 4), (4, 3), (4, 4)\right)\).
- Clasificar\(x\) y\(y\) por tipo y nivel de medición.
- Esbozar la gráfica de dispersión.
Construir una tabla con filas correspondientes a casos y columnas correspondientes a\(i\),,\(x_i\),\(y_i\),\(x_i - m(\bs{x})\),\(y_i - m(\bs{y})\),\([x_i - m(\bs{x})]^2\),\([y_i - m(\bs{y})]^2\),,\([x_i - m(\bs{x})][y_i - m(\bs{y})]\),\(\hat{y}_i\),\(\hat{y}_i - m(\bs{y})\),\([\hat{y}_i - m(\bs{y})]^2\),\(y_i - \hat{y}_i\), y\((y_i - \hat{y}_i)^2\). Agrega una fila en la parte inferior para totales y medias. Utilice la aritmética de precisión.
- Completa las primeras 8 columnas.
- Encontrar la correlación muestral y el coeficiente de determinación.
- Encuentra la ecuación de regresión muestral.
- Completa la tabla.
- Verificar las identidades para las sumas de cuadrados.
Contestar
| \(i\) | \(x_i\) | \(y_i\) | \(x_i - m(\bs{x})\) | \(y_i - m(\bs{y})\) | \([x_i - m(\bs{x})]^2\) | \([y_i - m(\bs{y})]^2\) | \([x_i - m(\bs{x})][y_i - m(\bs{y})]\) | \(\hat{y}_i\) | \(\hat{y}_i - m(\bs{y})\) | \([\hat{y}_i - m(\bs{y})]^2\) | \(y_i - \hat{y}_i\) | \((y_i - \hat{y}_i)^2\) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | \(-3\) | \(-2\) | \(9\) | \(4\) | \(6\) | \(9/7\) | \(-12/7\) | \(144/49\) | \(-2/7\) | \(4/49\) |
| 2 | 3 | 3 | \(-1\) | \(0\) | \(1\) | \(0\) | \(0\) | \(17/7\) | \(-4/7\) | \(16/49\) | \(4/7\) | \(16/49\) |
| 3 | 6 | 4 | \(2\) | \(1\) | \(4\) | \(1\) | \(2\) | \(29/7\) | \(8/7\) | \(64/49\) | \(-1/7\) | \(1/49\) |
| 4 | 2 | 1 | \(-2\) | \(-2\) | \(4\) | \(4\) | \(4\) | \(13/7\) | \(-8/7\) | \(64/49\) | \(-6/7\) | \(36/49\) |
| 5 | 8 | 5 | \(4\) | \(2\) | \(16\) | \(4\) | \(8\) | \(37/7\) | \(16/7\) | \(256/49\) | \(-2/7\) | \(4/49\) |
| 6 | 2 | 2 | \(-2\) | \(-1\) | \(4\) | \(1\) | \(2\) | \(13/7\) | \(-8/7\) | \(64/49\) | \(1/7\) | \(1/49\) |
| 7 | 4 | 3 | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(3\) | \(0\) | \(0\) | \(0\) | \(0\) |
| 8 | 6 | 4 | \(2\) | \(1\) | \(4\) | \(1\) | \(2\) | \(29/7\) | \(8/7\) | \(64/49\) | \(-1/7\) | \(1/49\) |
| 9 | 4 | 3 | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(3\) | \(0\) | \(0\) | \(0\) | \(0\) |
| 10 | 4 | 4 | \(0\) | \(1\) | \(0\) | \(1\) | \(0\) | \(3\) | \(0\) | \(0\) | \(1\) | \(1\) |
| Total | \(40\) | \(30\) | \(0\) | \(0\) | \(42\) | \(16\) | \(24\) | \(30\) | \(0\) | \(96/7\) | \(0\) | \(16/7\) |
| Media | \(4\) | \(3\) | \(0\) | \(0\) | \(14/3\) | \(16/9\) | \(8/3\) | \(3\) | \(0\) | \(96/7\) | \(0\) | \(2/7\) |
- discreto, relación
- \(r = 2 \sqrt{3/14} \approx 0.926\),\(r^2 = 6/7\)
- \(y = 3 + \frac{4}{7}(x - 4)\)
- \(16 = 96/7 + 16/7\)
Los dos ejercicios siguientes deberían ayudarte a revisar algunos de los temas de probabilidad en esta sección.
Supongamos que\((X, Y)\) tiene una distribución continua con función de densidad de probabilidad\(f(x, y) = 15 x^2 y\) para\(0 \le x \le y \le 1\). Encuentra cada uno de los siguientes:
- \(\mu = \E(X)\)y\(\nu = \E(Y)\)
- \(\sigma^2 = \var(X)\)y\(\tau^2 = \var(Y)\)
- \(\sigma_3 = \E\left[(X - \mu)^3\right]\)y\(\tau_3 = \E\left[(Y - \nu)^3\right]\)
- \(\sigma_4 = \E\left[(X - \mu)^4\right]\)y\(\tau_4 = \E\left[(Y - \nu)^4\right]\)
- \(\delta = \cov(X, Y)\),\(\rho = \cor(X, Y)\), y\(\delta_2 = \E\left[(X - \mu)^2 (Y - \nu)^2\right]\)
- \(L(Y \mid X)\)y\(L(X \mid Y)\)
Contestar
- \(5/8\),\(5/6\)
- \(17/448\),\(5/252\)
- \(-5/1792\),\(-5/1512\)
- \(305/86\,016\),\(5/3024\)
- \(5/336\),\(\sqrt{5/17}\),\(1/768\)
- \(L(Y \mid X) = \frac{10}{17} + \frac{20}{51} X\),\(L(X \mid Y) = \frac{3}{4} Y\)
Supongamos ahora que\(\left((X_1, Y_1), (X_2, Y_2), \ldots (X_9, Y_9)\right)\) es una muestra aleatoria de tamaño\(9\) a partir de la distribución en el ejercicio anterior. Encuentra cada uno de los siguientes:
- \(\E[M(\bs{X})]\)y\(\var[M(\bs{X})]\)
- \(\E[M(\bs{Y})]\)y\(\var[M(\bs{Y})]\)
- \(\cov[M(\bs{X}), M(\bs{Y})]\)y\(\cor[M(\bs{X}), M(\bs{Y})]\)
- \(\E[W^2(\bs{X})]\)y\(\var[W^2(\bs{X})]\)
- \(\E[W^2(\bs{Y})]\)y\(\var[W^2(\bs{Y})]\)
- \(\E[S^2(\bs{X})]\)y\(\var[S^2(\bs{X})]\)
- \(\E[S^2(\bs{Y})]\)y\(\var[S^2(\bs{Y})]\)
- \(\E[W(\bs{X}, \bs{Y})]\)y\(\var[W(\bs{X}, \bs{Y})]\)
- \(\E[S(\bs{X}, \bs{Y})]\)y\(\var[S(\bs{X}, \bs{Y})]\)
Contestar
- \(5/8\),\(17/4032\)
- \(5/6\),\(5/2268\)
- \(5/3024\),\(\sqrt{5/17}\)
- \(17/448\),\(317/1\,354\,752\)
- \(5/252\),\(5/35\,721\)
- \(17/448\),\(5935/21\,676\,032\)
- \(5/252\),\(115/762\,048\)
- \(5/336\),\(61/508\,032\)
- \(5/336\),\(181/1\,354\,752\)
Ejercicios de Análisis de Datos
Utilice software estadístico para los siguientes problemas.
Considere las variables de altura en los datos de altura de Pearson.
- Clasificar las variables por tipo y nivel de medición.
- Calcular el coeficiente de correlación y el coeficiente de determinación
- Calcular la línea de regresión de mínimos cuadrados, con la altura del padre como variable predictora y la altura del hijo como variable de respuesta.
- Dibuje la gráfica de dispersión y la línea de regresión juntas.
- Predecir la altura de un hijo cuyo padre mide 68 pulgadas de alto.
- Calcular la línea de regresión si las alturas se convierten a centímetros (hay 2.54 centímetros por pulgada).
Contestar
- Continuo, relación
- \(r = 0.501\),\(r^2 = 0.251\)
- \(y = 33.893 + 0.514 x\)
- 68.85
- \(y = 86.088 + 0.514 x\)
Considere las variables de longitud de pétalo, ancho de pétalo y especies en los datos del iris de Fisher.
- Clasificar las variables por tipo y nivel de medición.
- Calcular la correlación entre la longitud del pétalo y el ancho de los
- Calcular la correlación entre la longitud del pétalo y el ancho de los pétalos por especie
Contestar
- Especie: discreta, nominal; longitud y anchura del pétalo: relación continua
- 0.9559
- Setosa: 0.3316, Verginica: 0.3496, Versicolor: 0.6162
Considere el número de caramelos y las variables de peso neto en los datos de M&M.
- Clasificar la variable por tipo y nivel de medición.
- Calcular el coeficiente de correlación y el coeficiente de determinación.
- Calcular la línea de regresión de mínimos cuadrados con el número de caramelos como variable predictora y el peso neto como variable de respuesta.
- Dibuje la gráfica de dispersión y la línea de regresión en la parte (b) juntas.
- Predecir el peso neto de una bolsa de M&Ms con 56 caramelos.
- Ingenuamente, se podría esperar una correlación mucho más fuerte entre el número de caramelos y el peso neto en una bolsa de M&Ms. ¿Cuál es otra fuente de variabilidad en el peso neto?
Contestar
- Número de caramelos: discreto, relación; peso neto: continuo, relación
- \(r = 0.793\),\(r^2 = 0.629\)
- \(y = 20.278 + 0.507 x\)
- 48.657
- Variabilidad en el peso de los caramelos individuales.
Considerar la tasa de respuesta y las variables de puntaje total del SAT en el conjunto de datos SAT por estado.
- Clasificar las variables por tipo y nivel de medición.
- Calcular el coeficiente de correlación y el coeficiente de determinación.
- Calcular la línea de regresión de mínimos cuadrados con la tasa de respuesta como variable predictora y la puntuación SAT como variable de respuesta.
- Dibuje la gráfica de dispersión y la línea de regresión juntas.
- Dar una posible explicación de la correlación negativa.
Contestar
- Tasa de respuesta: continua, ratio. El puntaje SAT probablemente podría considerarse discreto o continuo, pero es solo en el nivel de intervalo de medición, ya que las puntuaciones más pequeñas posibles son 400 (200 cada una en las porciones verbal y matemática).
- \(r = -0.849\),\(r^2 = 0.721\)
- \(y = 1141.5 - 2.1 x\)
- Los estados con baja tasa de respuesta pueden ser estados para los que el SAT es opcional. En ese caso, los estudiantes que toman el examen son los mejores estudiantes, con destino a la universidad. Por el contrario, los estados con altas tasas de respuesta pueden ser estados para los que el SAT es obligatorio. En ese caso, todos los estudiantes, incluidos los más débiles y no escolarizados, toman el examen.
Considere los puntajes verbales y matemáticos del SAT (para todos los estudiantes) en el conjunto de datos SAT por año.
- Clasificar las variables por tipo y nivel de medición.
- Calcular el coeficiente de correlación y el coeficiente de determinación.
- Calcular la línea de regresión de mínimos cuadrados.
- Dibuje la gráfica de dispersión y la línea de regresión juntas.
Contestar
- Continuo quizás, pero sólo en el nivel de intervalo de medición debido a que la puntuación más pequeña posible en cada parte es 200.
- \(r = 0.614\),\(r^2 = 0.377\)
- \(y = 321.5 + 0.3 \, x\)
Considere las variables de temperatura y erosión en el primer conjunto de datos en los datos de Challenger.
- Clasificar las variables por tipo y nivel de medición.
- Calcular el coeficiente de correlación y el coeficiente de determinación.
- Calcular la línea de regresión de mínimos cuadrados.
- Dibuja la gráfica de dispersión y la línea de regresión juntas.
- Predecir la erosión de la junta tórica con una temperatura de 31° F.
- ¿Es significativa la predicción en la parte (c)? Explique.
- Encuentra la línea de regresión si la temperatura se convierte a grados Celsius. Recordemos que la conversión es\(\frac{5}{9}(x - 32)\).
Contestar
- temperatura: continua, intervalo; erosión: relación continua
- \(r = -0.555\),\(r^2 = 0.308\)
- \(y = 106.8 - 1.414 x\)
- 62.9.
- Esta estimación es problemática, ya que 31° está muy fuera del rango de los datos de la muestra.
- \(y = 61.54 - 2.545 x\)


