10.2: La paradoja de Bertrand
- Page ID
- 151969
Preliminares
Declaración del problema
El problema de Bertrand es encontrar la probabilidad de que un acorde aleatorio
en un círculo sea más largo que la longitud de un lado del triángulo equilátero inscrito. El problema lleva el nombre del matemático francés Joseph Louis Bertrand, quien estudió el problema en 1889.
Resulta, como veremos, que hay (al menos) tres respuestas al problema de Bertrand, dependiendo de cómo se interprete la frase acorde aleatorio
. La falta de una respuesta única se consideró una paradoja en su momento, porque se asumió (ingenuamente, en retrospectiva) que debía haber una sola respuesta natural.
Ejecuta el experimento de Bertrand 100 veces para cada uno de los siguientes modelos. No se preocupe por el significado exacto de los modelos, pero vea si puede detectar una diferencia en el comportamiento de los resultados
- Distancia uniforme
- Ángulo uniforme
- Punto final uniforme
Formulación Matemática
Para formular el problema matemáticamente, tomemos\((0, 0)\) como centro del círculo y tomemos el radio del círculo para que sea 1. Estos supuestos no implican pérdida de generalidad porque equivalen a medir distancias relativas al centro del círculo, y tomar el radio del círculo como unidad de longitud. Ahora considera un acorde en el círculo. Al girar el círculo, podemos suponer que un punto del acorde es\((1, 0)\) y el otro punto es\((X, Y)\) donde\(Y \gt 0\) y\(X^2 + Y^2 = 1\).
Con estos supuestos, el acorde se especifica completamente dando cualquiera de las siguientes variables
- La distancia (perpendicular)\(D\) desde el centro del círculo hasta el punto medio de la cuerda. Tenga en cuenta que\(0 \le D \le 1\).
- El ángulo\(A\) entre el\(x\) eje y la línea desde el centro del círculo hasta el punto medio de la cuerda. Tenga en cuenta que\(0 \le A \le \pi / 2\).
- La coordenada horizontal\(X\). Tenga en cuenta que\(-1 \le X \le 1\).
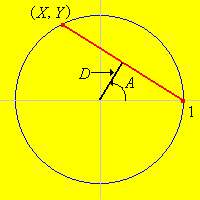
Las variables se relacionan de la siguiente manera:
- \(D = \cos(A)\)
- \(X = 2 D^2 - 1\)
- \(Y = 2 D \sqrt{1 - D^2}\)
Las relaciones inversas se dan a continuación. Tenga en cuenta nuevamente que hay correspondencias uno a uno entre\(X\),\(A\), y\(D\).
- \(A = \arccos(D)\)
- \(D = \sqrt{\frac{1}{2}(x + 1)}\)
- \(D = \sqrt{\frac{1}{2} \pm \frac{1}{2} \sqrt{1 - y^2} }\)
Si el acorde se genera de manera probabilística,,\(D\)\(A\)\(X\), y\(Y\) se convierten en variables aleatorias. A la luz de los resultados anteriores, especificando la distribución de cualquiera de las variables\(D\)\(A\), o determina\(X\) completamente la distribución de las cuatro variables.
El ángulo\(A\) es también el ángulo entre la cuerda y la línea tangente al círculo en\((1, 0)\).
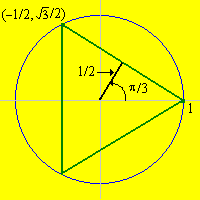
Ahora considera el triángulo equilátero inscrito en el círculo para que uno de los vértices sea\((1, 0)\). Considera el acorde definido por el lado superior del triángulo.
Para esta cuerda, las variables de ángulo, distancia y coordenadas se dan de la siguiente manera:
- \(a = \pi / 3\)
- \(d = 1 / 2\)
- \(x = -1 / 2\)
- \(y = \sqrt{3} / 2\)
Ahora supongamos que se elige un acorde de manera probabilística.
La longitud de la cuerda es mayor que la longitud de un lado del triángulo equilátero inscrito si y solo si ocurren las siguientes condiciones equivalentes:
- \(0 \lt D \lt 1 / 2\)
- \(\pi / 3 \lt A \lt \pi / 2\)
- \(-1 \lt X \lt -1 / 2\)
Modelos
Cuando un objeto se genera al azar
, una secuencia de variables naturales
que determina el objeto debe recibir una distribución uniforme apropiada. Las coordenadas del centro de la moneda son tal secuencia en el experimento de monedas de Buffon; las variables de ángulo y distancia son tal secuencia en el experimento de aguja de Buffon. El quid de la paradoja de Bertrand es el hecho de que la distancia\(D\), el ángulo\(A\) y la coordenada\(X\) cada uno parece ser una variable natural que determina la cuerda, pero se obtienen diferentes modelos, dependiendo de cuál se le dé la distribución uniforme.
El modelo con distancia uniforme
Supongamos que\(D\) se distribuye uniformemente en el intervalo\([0, 1]\).
La solución del problema de Bertrand es\[ \P \left( D \lt \frac{1}{2} \right) = \frac{1}{2} \]
En el experimento de Bertrand, seleccione el modelo de distancia uniforme. Ejecute el experimento 1000 veces y compare la función de frecuencia relativa del evento acorde con la probabilidad verdadera.
El ángulo\(A\) tiene función de densidad de probabilidad\[ g(a) = \sin(a), \quad 0 \lt a \lt \frac{\pi}{2} \]
Prueba
Esto se desprende de la norma la fórmula de cambio de variables.
La coordenada\(X\) tiene función de densidad de probabilidad\[ h(x) = \frac{1}{\sqrt{8 (x + 1)}}, \quad -1 \lt x \lt 1 \]
Prueba
Esto se desprende de la norma la fórmula de cambio de variables.
Tenga en cuenta que\(A\) y\(X\) no tienen distribuciones uniformes. Recordemos que un número aleatorio es una simulación de una variable con la distribución uniforme estándar, es decir, la distribución uniforme continua en el intervalo\( [0, 1) \).
Muestra cómo simular\(D\),,\(A\)\(X\), y\(Y\) usando un número aleatorio.
Contestar
\(A = \arccos(D)\),\(X = 2 D^2 - 1\),\(Y = 2 D \sqrt{1 - D^2}\), donde\(D\) es un número aleatorio
El modelo con ángulo uniforme
Supongamos que\(A\) se distribuye uniformemente en el intervalo\((0, \pi / 2)\).
La solución del problema de Bertrand es\[ \P\left(A \gt \frac{\pi}{3} \right) = \frac{1}{3} \]
En el experimento de Bertrand, seleccione el modelo de ángulo uniforme. Ejecute el experimento 1000 veces y compare la función de frecuencia relativa del evento acorde con la probabilidad verdadera.
La distancia\(D\) tiene función de densidad de probabilidad\[ f(d) = \frac{2}{\pi \sqrt{1 - d^2}}, \quad 0 \lt d \lt 1 \]
Prueba
Esto se desprende de la fórmula estándar de cambio de variables.
La coordenada\(X\) tiene función de densidad de probabilidad\[ h(x) = \frac{1}{\pi \sqrt{1 - x^2}}, \quad -1 \lt x \lt 1 \]
Prueba
Esto se desprende de la fórmula de cambio de variables.
Tenga en cuenta que\(D\) y\(X\) no tienen distribuciones uniformes.
Muestra cómo simular\(D\),,\(A\)\(X\), y\(Y\) usando un número aleatorio.
Contestar
\(A = \frac{\pi}{2} U\),\(D = \cos(A)\),\(X = 2 D^2 - 1\),\(Y = 2 D \sqrt{1 - D^2}\), donde\(U\) es un número aleatorio.
El modelo con punto final uniforme
Supongamos que\(X\) se distribuye uniformemente en el intervalo\((-1, 1)\).
La solución del problema de Bertrand es\[ \P \left( -1 \lt X \lt -\frac{1}{2} \right) = \frac{1}{4} \]
En el experimento de Bertrand, seleccione el modelo de punto final uniforme. Ejecute el experimento 1000 veces y compare la función de frecuencia relativa del evento acorde con la probabilidad verdadera.
La distancia\(D\) tiene función de densidad de probabilidad\[ f(d) = 2 d, \quad 0 \lt d \lt 1 \]
Prueba
Esto se desprende de la fórmula de cambio de variables.
El ángulo\(A\) tiene función de densidad de probabilidad\[ g(a) = 2 \sin(a) \cos(a), \quad 0 \lt a \lt \frac{\pi}{2} \]
Prueba
Esto se desprende de la fórmula de cambio de variables.
Tenga en cuenta que\(D\) y\(A\) no tienen distribuciones uniformes; de hecho,\(D\) tiene una distribución beta con el parámetro izquierdo 2 y el parámetro derecho 1.
Experimentos Físicos
Supongamos que se genera un acorde aleatorio arrojando una moneda de radio 1 sobre una tabla reglada con líneas paralelas que están separadas a la distancia 2. ¿Cuál de los modelos (si los hubiera) se aplicaría a este experimento físico?
Contestar
Distancia uniforme
Supongamos que una aguja está adherida al borde del disco de radio 1. Se genera un acorde aleatorio al girar la aguja. ¿Cuál de los modelos (si los hubiera) se aplicaría a este experimento físico?
Contestar
Ángulo uniforme
Supongamos que se construye un canal delgado en el borde de un disco de radio 1. Hacer rodar una bola en el canal genera un punto aleatorio en el círculo, por lo que se genera un acorde aleatorio rodando la pelota dos veces. ¿Cuál de los modelos (si los hubiera) se aplicaría a este experimento físico?
Contestar
Ángulo uniforme


