12.6: El problema del cumpleaños
- Page ID
- 151923
Introducción
El modelo de muestreo
Al igual que en el modelo de muestreo básico, supongamos que seleccionamos\(n\) números al azar, con reemplazo, de la población\(D =\{1, 2, \ldots, m\}\). Por lo tanto, nuestro vector de resultado\(X_i\) es\(\bs{X} = (X_1, X_2, \ldots, X_n)\) donde está el número\(i\) th elegido. Recordemos que nuestra suposición básica de modelado\(\bs{X}\) es que se distribuye uniformemente en el espacio muestral\(S = D^n = \{1, 2, \ldots, m\}^n\)
En esta sección, nos interesa el número de valores poblacionales que faltan en la muestra, y el número de valores poblacionales (distintos) en la muestra. El cálculo de probabilidades relacionadas con estas variables aleatorias generalmente se conoce como problemas de cumpleaños. A menudo, interpretaremos el experimento de muestreo como una distribución de\(n\) bolas en\(m\) celdas;\(X_i\) es el número de celdas de bola\(i\). En esta interpretación, nuestro interés está en el número de celdas vacías y el número de celdas ocupadas.
Para\(i \in D\), vamos a\(Y_i\) denotar el número de veces que\(i\) ocurre en la muestra:\[ Y_i = \#\left\{j \in \{1, 2, \ldots, n\}: X_j = i\right\} = \sum_{j=1}^n \bs{1}(X_j = i) \]
\(\bs{Y} = (Y_1, Y_2, \ldots, Y_m)\)tiene la distribución multinomial con parámetros\(n\) y\((1/m, 1/m, \ldots, 1/m)\):\[\P(Y_1 = y_1, Y_2 = y_2, \ldots, Y_m = y_m) = \binom{n}{y_1, y_2, \ldots, y_n} \frac{1}{m^n}, \quad (y_1, y_2, \ldots, y_m) \in \N^n \text{ with } \sum_{i=1}^m y_i = n \]
Prueba
Esto se desprende inmediatamente de la definición de la distribución multinomial, ya que\((X_1, X_2, \ldots, X_n)\) es una secuencia independiente, y\(X_i\) se distribuye uniformemente\(\{1, 2, \ldots, m\}\) para cada uno\(i\).
Ahora definiremos las principales variables aleatorias de interés.
El número de valores de población que faltan en la muestra es\[ U = \#\left\{j \in \{1, 2, \ldots, m\}: Y_j = 0\right\} = \sum_{j=1}^m \bs{1}(Y_j = 0) \] y el número de valores de población (distintos) que ocurren en la muestra es\[ V = \#\left\{j \in \{1, 2, \ldots, m\}: Y_j \gt 0\right\} = \sum_{j=1}^m \bs{1}(Y_j \gt 0) \] También,\(U\) toma valores\(\{\max\{m - n, 0\}, \ldots, m - 1\}\) y\(V\) toma valores en\(\{1, 2, \ldots, \min\{m,n\}\}\).
Claramente debemos tener\(U + V = m\) así que una vez que tenemos la distribución de probabilidad y los momentos de una variable, podemos encontrarlos fácilmente para la otra variable. No obstante, primero resolveremos la versión más simple del problema del cumpleaños.
El simple problema del cumpleaños
El evento de que hay al menos una duplicación cuando se elige una muestra de tamaño\(n\) de una población de tamaño\(m\) es\[ B_{m,n} = \{V \lt n\} = \{U \gt m - n\} \] El problema de cumpleaños (simple) es calcular la probabilidad de este evento. Por ejemplo, supongamos que elegimos\(n\) personas al azar y anotamos sus cumpleaños. Si ignoramos los años bisiestos y asumimos que los cumpleaños se distribuyen uniformemente a lo largo del año, entonces nuestro modelo de muestreo aplica con\(m = 365\). En esta configuración, el problema del cumpleaños es calcular la probabilidad de que al menos dos personas tengan el mismo cumpleaños (este caso especial es el origen del nombre).
La solución del problema del cumpleaños es un ejercicio fácil de probabilidad combinatoria.
La probabilidad del evento de cumpleaños es\[ \P\left(B_{m,n}\right) = 1 - \frac{m^{(n)}}{m^n}, \quad n \le m \] y\(P\left(B_{m,n}\right) = 1\) para\(n \gt m\)
Prueba
El evento complementario\(B^c\) ocurre si y solo si el vector de resultado\(\bs{X}\) forma una permutación de tamaño\(n\) a partir de\(\{1, 2, \ldots, m\}\). El número de permutaciones es\(m^{(n)}\) y por supuesto el número de muestras es\(m^n\).
El hecho de que la probabilidad sea 1 para\(n \gt m\) algunas veces se conoce como el principio del palomo: si se colocan más de\(m\) palomas en\(m\) agujeros entonces al menos un hoyo tiene 2 o más palomas. El siguiente resultado da una relación de recurrencia para la probabilidad de valores de muestra distintos y, por lo tanto, da otra forma de calcular la probabilidad de cumpleaños.
\(p_{m,n}\)Denote la probabilidad del evento complementario de cumpleaños\(B^c\), de que las variables de muestra sean distintas, con tamaño poblacional\(m\) y tamaño muestral\(n\). Entonces\(p_{m,n}\) satisface la siguiente relación de recursión y condición inicial:
- \(p_{m,n+1} = \frac{m-n}{m} p_{m,n}\)
- \(p_{m,1} = 1\)
Ejemplos
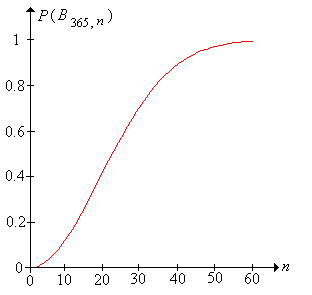
Let\(m = 365\) (el problema de cumpleaños estándar).
- \(\P\left(B_{365,10}\right) = 0.117\)
- \(\P\left(B_{365,20}\right) = 0.411\)
- \(\P\left(B_{365,30}\right) = 0.706\)
- \(\P\left(B_{365,40}\right) = 0.891\)
- \(\P\left(B_{365,50}\right) = 0.970\)
- \(\P\left(B_{365,60}\right) = 0.994\)
En el experimento de cumpleaños, establezca\(n = 365\) y seleccione la variable indicadora\(I\). Para\(n \in \{10, 20, 30, 40, 50, 60\}\) ejecutar el experimento 1000 veces cada uno y comparar las frecuencias relativas con las probabilidades verdaderas.
A pesar de su fácil solución, el problema del cumpleaños es famoso porque, numéricamente, las probabilidades pueden ser un poco sorprendentes. Tenga en cuenta que con solo 60 personas, ¡el evento es casi seguro! Con apenas 23 personas, el evento de cumpleaños se trata\( \frac{1}{2} \); específicamente\( \P(B_{365,23}) = 0.507 \). Matemáticamente, el rápido aumento en la probabilidad de cumpleaños, a medida que\(n\) aumenta, se debe a que\(m^n\) crece mucho más rápido que\(m^{(n)}\).
Se rotan cuatro dados justos y estándar. Encuentra la probabilidad de que las puntuaciones sean distintas.
Contestar
\(\frac{5}{18}\)
En el experimento de cumpleaños, establezca\(m = 6\) y seleccione la variable indicadora\(I\). Varíe\(n\) con la barra de desplazamiento y anote gráficamente cómo cambian las probabilidades. Ahora con\(n = 4\), ejecute el experimento 1000 veces y compare la frecuencia relativa del evento con la probabilidad correspondiente.
Cinco personas son elegidas al azar.
- Encuentra la probabilidad de que al menos 2 tengan el mismo mes de nacimiento.
- Criticar el modelo de muestreo en este escenario
Contestar
- \( \frac{89}{144} \)
- El número de días en un mes varía, por lo que la suposición de que el mes de nacimiento de una persona se distribuye uniformemente a lo largo de los 12 meses no del todo exacto.
En el experimento de cumpleaños, establezca\(m = 12\) y seleccione la variable indicadora\(I\). Varíe\(n\) con la barra de desplazamiento y anote gráficamente cómo cambian las probabilidades. Ahora con\(n = 5\), ejecute el experimento 1000 veces y compare la frecuencia relativa del evento con la probabilidad correspondiente.
Un restaurante de comida rápida regala uno de los 10 juguetes diferentes con la compra de una comida infantil. Una familia con 5 hijos compra 5 comidas infantiles. Encuentra la probabilidad de que los 5 juguetes sean diferentes.
Contestar
\(\frac{189}{625}\)
En el experimento de cumpleaños, establezca\(m = 10\) y seleccione la variable indicadora\(I\). Varíe\(n\) con la barra de desplazamiento y anote gráficamente cómo cambian las probabilidades. Ahora con\(n = 5\), ejecute el experimento 1000 veces y comparela frecuencia relativa del evento con la probabilidad correspondiente.
Vamos\(m = 52\). Encuentra el valor más pequeño de\(n\) tal que la probabilidad de una duplicación sea al menos\(\frac{1}{2}\).
Contestar
\(n = 9\)
El problema general del cumpleaños
Ahora volvemos al problema más general de encontrar la distribución del número de valores de muestra distintos y la distribución del número de valores de muestra excluidos.
La función de densidad de probabilidad
El número de muestras con\(j\) valores exactamente excluidos es\[ \#\{U = j\} = \binom{m}{j} \sum_{k=0}^{m-j} (-1)^k \binom{m - j}{k}(m - j - k)^n, \quad j \in \{\max\{m-n, 0\}, \ldots, m - 1\} \]
Prueba
Para\(i \in D\), considere el evento que\(i\) no ocurre en la muestra:\(A_i = \{Y_i = 0\}\). Ahora vamos\(K \subseteq D\) con\(\#(K) = k\). Usando la regla de multiplicación de combinatoria, es fácil contar el número de muestras que no contienen ningún elemento de\(K\):\[ \#\left(\bigcap_{i \in K} A_i\right) = (m - k)^n \] Ahora la regla de inclusión-exclusión de combinatoria se puede utilizar para contar el número de muestras a las que les falta al menos un valor poblacional:\[ \#\left(\bigcup_{i=1}^m A_i\right) = \sum_{k=1}^m (-1)^{k-1} \binom{m}{k}(m - k)^n \] Una vez que tenemos esto, podemos usar la ley de DeMorgan para contar el número de muestras que contienen todos los valores de población:\[ \#\left(\bigcap_{i=1}^m A_i^c\right) = \sum_{k=0}^m (-1)^k \binom{m}{k} (m - k)^n \] Ahora podemos usar un procedimiento de dos pasos para generar todas las muestras que excluyan exactamente los valores de\(j\) población: Primero, elija los\(j\) valores que se van a excluir. El número de formas de realizar este paso es\(\binom{m}{j}\). A continuación, seleccione una muestra de tamaño\(n\) de los valores restantes de la población para que no se excluya ninguna. El número de formas de realizar este paso es el resultado en la última ecuación mostrada, pero con\(m - j\) reemplazo\(m\). El principio de multiplicación de la combinatoria da el resultado.
Las distribuciones del número de valores excluidos y el número de valores distintos son ahora fáciles.
La función de densidad de probabilidad de\(U\) viene dada por\[ \P(U = j) = \binom{m}{j} \sum_{k=0}^{m-j} (-1)^k \binom{m-j}{k}\left(1 - \frac{j + k}{m}\right)^n, \quad j \in \{\max\{m-n,0\}, \ldots, m-1\} \]
Prueba
Ya que las muestras están distribuidas uniformemente,\(\P(U = j) = \#\{U = j\} / m^n\) y así el resultado se desprende del ejercicio anterior.
La función de densidad de probabilidad del número de valores distintos\(V\) viene dada por\[ \P(V = j) = \binom{m}{j} \sum_{k=0}^j (-1)^k \binom{j}{k} \left(\frac{j - k}{m}\right)^n, \quad j \in \{1, 2, \ldots, \min\{m,n\}\} \]
Prueba
Esto se desprende del teorema anterior ya que\(\P(V = j) = \P(U = m - j).\)
En el experimento de cumpleaños, seleccione el número de valores de muestra distintos. Varíe los parámetros y anote la forma y ubicación de la función de densidad de probabilidad. Para valores seleccionados de los parámetros, ejecute la simulación 1000 y compare la función de frecuencia relativa con la función de densidad de probabilidad.
La distribución del número de valores excluidos también se puede obtener mediante un argumento de recursión.
Dejar\(f_{m,n}\) denotar la función de densidad de probabilidad del número de valores excluidos\(U\), cuando el tamaño de la población es\(m\) y el tamaño de la muestra es\(n\). Entonces
- \(f_{m,1}(m - 1) = 1\)
- \(f_{m,n+1}(j) = \frac{m - j}{m} f_{m,n}(j) + \frac{j+1}{m} f_{m,n}(j+1)\)
Momentos
Ahora encontraremos los medios y varianzas. El número de valores excluidos y el número de valores distintos son variables de conteo y por lo tanto pueden escribirse como sumas de variables indicadoras. Como hemos visto en muchos otros modelos, esta representación suele ser la mejor para momentos informáticos.
Para\(j \in \{0, 1, \ldots, m\}\), let\(I_j = \bs{1}(Y_j = 0)\), la variable indicadora del evento que no\(j\) está en la muestra. Tenga en cuenta que el número de valores de población que faltan en la muestra se puede escribir como la suma de las variables indicadoras:\[ U = \sum_{j=1}^m I_j \]
Para distintos\(i, \, j \in \{1, 2, \ldots, m\}\),
- \(E\left(I_j\right) = \left(1 - \frac{1}{m}\right)^n\)
- \(\var\left(I_j\right) = \left(1 - \frac{1}{m}\right)^n - \left(1 - \frac{1}{m}\right)^{2\,n}\)
- \(\cov\left(I_i, I_j\right) = \left(1 - \frac{2}{m}\right)^n - \left(1 - \frac{1}{m}\right)^{2\,n}\)
Prueba
Dado que cada valor poblacional es igualmente probable que se elija,\(\P(I_j = 1) = (1 - 1 / m)^n\). Así, las partes (a) y (b) se derivan de resultados estándar para la media y varianza de una variable indicadora. A continuación,\(I_i I_j\) se encuentra la variable indicadora del evento que\(i\) y ambos\(j\) están excluidos, así\(\P(I_i I_j = 1) = (1 - 2 / m)^n\). A continuación, la parte (c) sigue de la fórmula estándar para la covarianza.
El número esperado de valores excluidos y el número esperado de valores distintos son
- \(\E(U) = m \left(1 - \frac{1}{m}\right)^n\)
- \(\E(V) = m \left[1 - \left(1 - \frac{1}{m}\right)^n \right]\)
Prueba
La parte (a) se desprende de la exericse anterior y de la representación\(U = \sum_{j=1}^n I_j\). La parte b) se desprende de la parte (a) ya que\(U + V = m\).
La varianza del número de valores exludidos y la varianza del número de valores distintos son\[ \var(U) = \var(V) = m (m - 1) \left(1 - \frac{2}{m}\right)^n + m \left(1 - \frac{1}{m}\right)^n - m^2 \left(1 - \frac{1}{m}\right)^{2 n} \]
Prueba
Recordemos eso\(\var(U) = \sum_{i=1}^m \sum_{j=1}^m \cov(I_i, I_j)\). Usando los resultados anteriores sobre la covarianza de las variables indicadoras y simplificando da la varianza de\(U\). También,\(\var(V) = \var(U)\) ya que\(U + V = m\).
En el experimento de cumpleaños, seleccione el número de valores de muestra distintos. Varíe los parámetros y anote el tamaño y la ubicación de la barra de\( \pm \) desviación estándar media. Para valores seleccionados de los parámetros, ejecute la simulación 1000 veces y compare la media y varianza de la muestra con la media de distribución y varianza.
Ejemplos y Aplicaciones
Supongamos que 30 personas son elegidas al azar. Encuentra cada uno de los siguientes:
- La función de densidad de probabilidad del número de cumpleaños distintos.
- La media del número de cumpleaños distintos.
- La varianza del número de cumpleaños distintos.
- La probabilidad de que haya por lo menos 28 cumpleaños diferentes representados.
Contestar
- \(\P(V = j) = \binom{30}{j} \sum_{k=0}^j (-1)^k \left(\frac{j-k}{365}\right)^{30}, \quad j \in \{1, 2, \ldots, 30\}\)
- \(\E(V) = 28.8381\)
- \(\var(V) = 1.0458\)
- \(\P(V \ge 28) = 0.89767\)
En el experimento de cumpleaños, set\( m = 365 \) y\( n = 30 \). Ejecutar el experimento 1000 veces con una frecuencia de actualización de 10 y calcular la frecuencia relativa del evento en la parte (d) del último ejercicio.
Supongamos que se rodan 10 dados justos. Encuentra cada uno de los siguientes:
- La función de densidad de probabilidad del número de puntuaciones distintas.
- La media del número de puntuaciones distintas.
- La varianza del número de puntuaciones distintas.
- La probabilidad de que haya 4 o menos puntuaciones distintas.
Contestar
- \(\P(V = j) = \binom{10}{j} \sum_{k=0}^j (-1)^k \binom{j}{k} \left(\frac{j-k}{6}\right)^{10}, \quad j \in \{1, 2, \ldots, 6\}\)
- \(\E(V) = 5.0310\)
- \(\var(V) = 0.5503\)
- \(\P(V \le 4) = 0.22182\)
En el experimento de cumpleaños, set\(m = 6\) y\(n = 10\). Ejecutar el experimento 1000 veces y calcular la frecuencia relativa del evento en la parte (d) del último ejercicio.
Un restaurante de comida rápida regala uno de los 10 juguetes diferentes con la compra de cada comida infantil. Una familia compra 15 comidas infantiles. Encuentra cada uno de los siguientes:
- La función de densidad de probabilidad del número de juguetes que faltan.
- La media del número de juguetes que faltan.
- La varianza del número de juguetes que faltan.
- La probabilidad de que falten al menos 3 juguetes.
Contestar
- \(\P(U = j) = \binom{15}{j} \sum_{k=0}^{10-j} (-1)^k \binom{10-j}{k}\left(1 - \frac{j+k}{10}\right)^{15}, \quad j \in \{0, 1, \ldots, 9\}\)
- \(\E(U) = 2.0589\)
- \(\var(U) = 0.9864\)
- \(\P(U \ge 3) = 0.3174\)
En el experimento de cumpleaños, set\(m = 10\) y\(n = 15\). Ejecutar el experimento 1000 veces y calcular la frecuencia relativa del evento en la parte (d).
El problema de los estudiantes mentirosos. Supongamos que 3 alumnos, que cabalgan juntos, pierdan un examen de matemáticas. Deciden mentirle al instructor diciendo que el auto tenía una llanta deshilachada. El instructor separa a los alumnos y les pregunta a cada uno de ellos qué llanta estaba desmontada. Los alumnos, que no lo anticiparon, seleccionan sus respuestas de forma independiente y al azar. Encuentra cada uno de los siguientes:
- La función de densidad de probabilidad del número de respuestas distintas.
- La probabilidad de que los estudiantes se salgan con la suya con su engaño.
- La media del número de respuestas distintas.
- La desviación estándar del número de respuestas distintas.
Contestar
-
\(j\) 1 2 3 \(\P(V = j)\) \(\frac{1}{16}\) \(\frac{9}{16}\) \(\frac{6}{16}\) - \(\P(V = 1) = \frac{1}{16}\)
- \(\E(V) = \frac{37}{16}\)
- \(\sd(V) = \sqrt{\frac{87}{256}} \approx 0.58296\)
El problema del cazador de patos. Supongamos que hay 5 cazadores de patos, cada uno un tiro perfecto. Una bandada de 10 patos sobrevuela, y cada cazador selecciona un pato al azar y dispara. Encuentra cada uno de los siguientes:
- La función de densidad de probabilidad del número de patos que son asesinados.
- La media del número de patos que son asesinados.
- La desviación estándar del número de patos que se matan.
Contestar
-
\(j\) 1 2 3 4 5 \(\P(V = j)\) \(\frac{1}{10\,000}\) \(\frac{27}{2000}\) \(\frac{9}{50}\) \(\frac{63}{125}\) \(\frac{189}{625}\) - \(\E(V) = \frac{40\,951}{10\,000} = 4.0951\)
- \(\sd(V) = 0.72768\)


